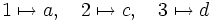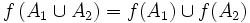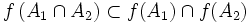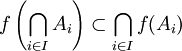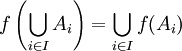Image Directe

Image Directe

Image directe

L'image directe d'un sous-ensemble A de X par une application 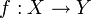f:X\rightarrow Y est le sous-ensemble de Y formé des éléments qui ont au moins un antécédent par f d'un élément de A :

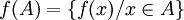f(A) = \{f(x) / x \in A\},
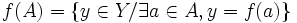ou f(A) = \{y \in Y / \exists a \in A, y=f(a)\}.

Si A=X, alors f(X) est appelée l'image de (l'application) f.

On se gardera bien de confondre l'image directe par f d'une partie de X, avec l'image par f d'un élément x de X.

Exemple : Considérons l'application 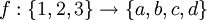f:\{1, 2, 3\}\rightarrow \{a, b, c, d\}, définie par

1\mapsto a, \quad 2\mapsto c, \quad 3\mapsto d

L'image directe de {2,3} par f est f({2,3})={c,d} tandis que l'image de f est {a,c,d}.

Propriétés élémentaires

  • Pour toutes parties A1 et A2 de X,
f\left(A_1 \cup A_2\right) = f(A_1) \cup f(A_2)
f\left(A_1 \cap A_2\right) \subset f(A_1) \cap f(A_2)

L'inclusion dans l'autre sens est fausse en général. Considérons l'unique application 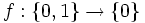f:\{0,1\}\rightarrow \{0\}. L'image par f de toute partie non vide est le singleton {0}.

\left[ \forall A_1 \subset X, \forall A_2 \subset X, f\left(A_1 \cap A_2\right) = f(A_1) \cap f(A_2)\right] \Leftrightarrow f\ {\rm injective}.
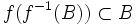  • pour toute partie B de Y, f(f^{-1}(B)) \subset B.
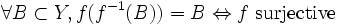\forall B \subset Y, f(f^{-1}(B)) = B \Leftrightarrow f \ {\rm surjective}.
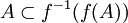
  • pour toute partie A de X, A\subset f^{-1}(f(A))
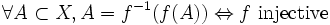\forall A \subset X, A = f^{-1}(f(A)) \Leftrightarrow f \ {\rm injective}.
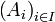  • Pour toute famille \left(A_i\right)_{i\in I} de parties de X,
f\left(\bigcap_{i\in I}A_i\right)\subset \bigcap_{i\in I}f(A_i)
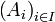  • Pour toute famille \left(A_i\right)_{i\in I} de parties de X,
f\left(\bigcup_{i\in I}A_i\right)= \bigcup_{i\in I}f(A_i)

Voir aussi

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Image directe ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Image Directe de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Image directe — L image directe d un sous ensemble A de X par une application est le sous ensemble de Y formé des éléments qui ont, par f, au moins un antécédent appartenant à A : . Exemples On définit en p …   Wikipédia en Français

  • Image Réciproque — L image réciproque d une partie B d un ensemble Y par une application est le sous ensemble de X constitué des éléments dont l image par f appartient à B : . Exemple : Considérons l application , définie par …   Wikipédia en Français

  • Image reciproque — Image réciproque L image réciproque d une partie B d un ensemble Y par une application est le sous ensemble de X constitué des éléments dont l image par f appartient à B : . Exemple : Considérons l application , définie par …   Wikipédia en Français

  • IMAGE — Même limitée aux arts visuels, l’image ne peut être séparée des racines profondes qu’elle a dans la mémoire, l’imagination, la pensée ou le rêve. L’image est sans nul doute l’objet de réflexion le plus rebelle aux classifications par genres et… …   Encyclopédie Universelle

  • Image réciproque — L image réciproque d une partie B d un ensemble Y par une application f : X → Y est le sous ensemble de X constitué des éléments dont l image par f appartient à B : Sommaire 1 Exemples 2 …   Wikipédia en Français

  • Image (homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Image (homonymie) », sur le Wiktionnaire (dictionnaire universel) Couramment, une image, du latin… …   Wikipédia en Français

  • Image d'une application — On appelle image d une application f (de l ensemble A vers l ensemble B) l image directe de A par f. C est donc le sous ensemble de B contenant toutes les images de tous les éléments de A et uniquement ces images. On le note Im(f). Exemple  …   Wikipédia en Français

  • directe — ● directe nom féminin Voie d ascension se rapprochant le plus possible de la ligne droite entre la base et le sommet de la montagne. ● direct, directe adjectif (latin directus, droit) Se dit d un trajet qui est sans détour, sans intermédiaire :… …   Encyclopédie Universelle

  • Image négative — Image Pour les articles homonymes, voir Image (homonymie). L ombre, une image naturelle Une image est une représentation visuelle voire mentale de quelque chose (objet, êtr …   Wikipédia en Français

  • Image — Pour les articles homonymes, voir Image (homonymie). L ombre portée, une image naturelle, différente de l original ; déjà métaphoriquement utilisée dans son « mythe de la caverne » par …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”