- Theoreme de Tychonov
-
Théorème de Tychonov
Le théorème de Tychonov est un théorème de topologie qui affirme qu'un produit d'espaces topologiques compacts est compact au sens de la topologie produit. Il a été publié en 1930 par le mathématicien russe Andreï Nikolaïevitch Tikhonov. Il a plusieurs applications en topologie algébrique et différentielle, particulièrement en analyse fonctionnelle, pour la preuve du théorème de Banach-Alaoglu-Bourbaki et le compactifié de Stone-Čech.
Si ce théorème ne choque pas l'intuition dans le cas d'un produit fini, sa validité dans le cas d'un produit quelconque est plus étonnante, et se démontre par une méthode non constructive faisant appel à l'axiome du choix. On notera qu'il est aussi possible de se passer de l'axiome du choix dans le cas d'un produit dénombrable d'espaces métriques compacts, ce que nous montrons dans la première partie de cet article, la deuxième étant consacrée à la démonstration dans le cas général.
Sommaire
Démonstration dans le cas d'un produit dénombrable de métriques
Dans le cas du produit dénombrable de métriques, l'idée essentielle est de faire de ce produit un espace lui aussi métrique en le munissant d'une distance appropriée, ce qui permet ensuite d'utiliser le théorème de Bolzano-Weierstrass: le produit X sera compact si et seulement si de toute suite d'éléments de X on peut extraire une sous-suite convergente.
DémonstrationSoit donc
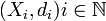 une famille de métriques compacts. On se ramène à des distances di plus petites que 1: pour chaque i, la distance d'i = Min(di,1) définit la même topologie que la distance di. Définissons sur
une famille de métriques compacts. On se ramène à des distances di plus petites que 1: pour chaque i, la distance d'i = Min(di,1) définit la même topologie que la distance di. Définissons sur 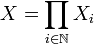 l'application d par:
l'application d par: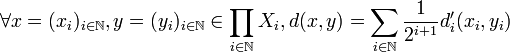
On vérifiera aisément que c'est bien une distance sur X. Montrons qu'elle définit les mêmes ouverts de la topologie produit.
Soit
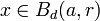 , montrons que x appartient à un ouvert pour la topologie produit contenu dans Bd(a,r). Par l'inégalité triangulaire, il existe ρ > 0 tel que
, montrons que x appartient à un ouvert pour la topologie produit contenu dans Bd(a,r). Par l'inégalité triangulaire, il existe ρ > 0 tel que 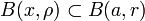 . La série
. La série 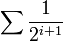 est absolument convergente: son reste tend donc vers 0. Soit donc N tel que
est absolument convergente: son reste tend donc vers 0. Soit donc N tel que 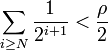 . On considère alors l'ouvert
. On considère alors l'ouvert 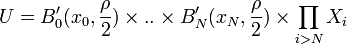 , si
, si 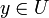 alors
alors 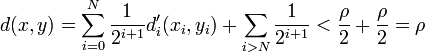 donc U voisinage au sens de la topologie produit de x inclus dans Bd(a,r): la topologie produit contient donc la topologie métrique.
donc U voisinage au sens de la topologie produit de x inclus dans Bd(a,r): la topologie produit contient donc la topologie métrique.Réciproquement, soit U ouvert de la topologie produit, soit
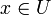 , alors il existe
, alors il existe 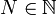 et r0..rN > 0 tels que
et r0..rN > 0 tels que 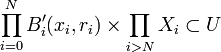 . On considère alors le rayon
. On considère alors le rayon 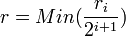 : la boule pour d de centre x et de rayon r est alors incluse dans U: en effet sid(x,y) < r, alors
: la boule pour d de centre x et de rayon r est alors incluse dans U: en effet sid(x,y) < r, alors 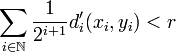 , comme la somme est à termes positifs chaque terme est donc plus petit que r:
, comme la somme est à termes positifs chaque terme est donc plus petit que r: 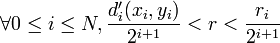 donc
donc 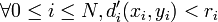 , donc
, donc 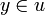 . U est donc voisinage de chacun de ses points au sens de la topologie métrique: c'est donc un ouvert de la topologie métrique: la topologie métrique contient la topologie produit.
. U est donc voisinage de chacun de ses points au sens de la topologie métrique: c'est donc un ouvert de la topologie métrique: la topologie métrique contient la topologie produit.Ainsi, la topologie métrique et la topologie produit sont égales. On peut alors utiliser pour la compacité de X la caractérisation séquentielle par un procédé diagonal: soit
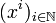 une suite d'éléments de X (une suite de suites). La suite
une suite d'éléments de X (une suite de suites). La suite 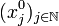 admet une suite extraite
admet une suite extraite 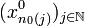 qui converge vers
qui converge vers 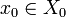 par compacité de X0. Alors la suite
par compacité de X0. Alors la suite 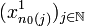 admet une suite extraite
admet une suite extraite 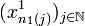 qui converge vers
qui converge vers 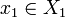 par compacité de X1, et n1 est une sous suite de n0 donc
par compacité de X1, et n1 est une sous suite de n0 donc 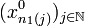 converge vers x0. Par récurrence, supposons qu'il existe une extractrice np telle que pour tout
converge vers x0. Par récurrence, supposons qu'il existe une extractrice np telle que pour tout 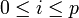 ,
, 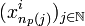 converge vers xi.
converge vers xi. 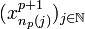 suite d'éléments de Xp + 1, donc admet une sous suite
suite d'éléments de Xp + 1, donc admet une sous suite 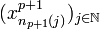 convergeant vers
convergeant vers 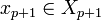 , avec np + 1 extraite de np, ce qui prouve la récurrence, or la propriété est vérifiée pour p=0 donc par récurrence on a l'existence d'éléments xi tels que pour tout p, il existe une extractrice np avec que pour tout
, avec np + 1 extraite de np, ce qui prouve la récurrence, or la propriété est vérifiée pour p=0 donc par récurrence on a l'existence d'éléments xi tels que pour tout p, il existe une extractrice np avec que pour tout 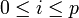 ,
, 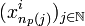 converge vers xi.
converge vers xi.L'extractrice
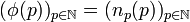 donne alors une suite extraite de
donne alors une suite extraite de 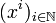 qui converge vers
qui converge vers 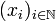 par construction, ce qui achève la preuve puisqu'on est dans un métrique.
par construction, ce qui achève la preuve puisqu'on est dans un métrique.Démonstration dans le cas général
On va utiliser la propriété de Borel-Lebesgue pour les fermés: un espaceX est compact si seulement si il est séparé et pour toute famille
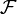 de fermés de X dont l'intersection finie d'éléments est non vide, alors:
de fermés de X dont l'intersection finie d'éléments est non vide, alors: 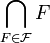 est non vide. Comme tout produit de séparés est séparé pour la topologie produit, il reste à prouver que le produit de compacts vérifie la propriété de Borel-Lebesgue, et ce en utilisant le lemme de Zorn.
est non vide. Comme tout produit de séparés est séparé pour la topologie produit, il reste à prouver que le produit de compacts vérifie la propriété de Borel-Lebesgue, et ce en utilisant le lemme de Zorn.Soit donc
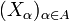 une famille de compacts, et soit
une famille de compacts, et soit 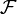 une famille de fermés de
une famille de fermés de 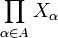 dont l'intersection finie d'éléments est non vide. On notera pα la projection sur Xα.
dont l'intersection finie d'éléments est non vide. On notera pα la projection sur Xα.On va considérer l'ensemble des familles contenant (au sens de l'inclusion)
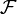 et dont les intersections finie d'éléments sont non vides: c'est un ensemble ordonné par l'inclusion et inductif: il vérifie donc les hypothèses du lemme de Zorn, et admet donc un élément maximal
et dont les intersections finie d'éléments sont non vides: c'est un ensemble ordonné par l'inclusion et inductif: il vérifie donc les hypothèses du lemme de Zorn, et admet donc un élément maximal 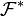 .
.Soit
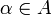 fixé. Comme l'intersection finie d'éléments de
fixé. Comme l'intersection finie d'éléments de 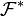 est non vide, c'est aussi le cas de l'intersection finie de projections sur Xα d'éléments de
est non vide, c'est aussi le cas de l'intersection finie de projections sur Xα d'éléments de 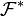 , donc de l'adhérence de tels éléments: ainsi la famille
, donc de l'adhérence de tels éléments: ainsi la famille 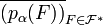 vérifie les hypothèses de la propriété de Borel-Lebesgue dans Xα compact, donc
vérifie les hypothèses de la propriété de Borel-Lebesgue dans Xα compact, donc 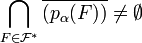 : soit donc xα élément de cette intersection.
: soit donc xα élément de cette intersection.On va alors considérer l'élément
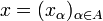 du produit et montrer qu'il est bien dans l'intersection des éléments de
du produit et montrer qu'il est bien dans l'intersection des éléments de 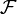 , qui sera alors non vide ce qui achèvera la preuve.
, qui sera alors non vide ce qui achèvera la preuve.On remarque tout d'abord que par maximalité, (L1):
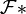 est stable par intersection finie: sinon il existe
est stable par intersection finie: sinon il existe 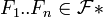 tels que
tels que 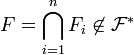 , alors l'intersection d'éléments de
, alors l'intersection d'éléments de 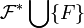 est non vide, et il contient
est non vide, et il contient 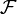 tout en étant strictement plus grand que
tout en étant strictement plus grand que 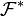 : absurde par maximalité de celui-ci.
: absurde par maximalité de celui-ci.Par un argument similaire, on en déduit que (L2): si un ensemble intersecte tous les éléments de
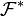 , alors il appartient à
, alors il appartient à 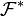 .
.Soit U ouvert de
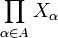 contenant x: il existe
contenant x: il existe 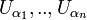 ouverts respectifs de
ouverts respectifs de 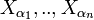 tels que
tels que 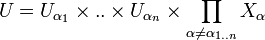 .
.Alors soit
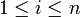 , on a
, on a 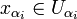 , ainsi
, ainsi 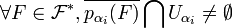 , or
, or 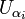 ouvert donc
ouvert donc 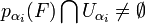 , donc
, donc 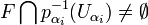 . Alors par (L2),
. Alors par (L2), 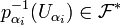 .
.Donc par (L1),
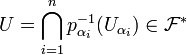 , donc U intersecte tous les éléments de
, donc U intersecte tous les éléments de 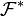 , a fortiori de
, a fortiori de 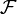 .
.Ainsi x est dans l'adhérence de tous les éléments de
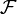 qui sont fermés, donc x appartient à tous les éléments de
qui sont fermés, donc x appartient à tous les éléments de 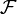 dont l'intersection est donc non vide, ce qui achève la preuve.
dont l'intersection est donc non vide, ce qui achève la preuve.Remarque
On peut donner une démonstration élégante [1] de ce théorème en utilisant la théorie des filtres
Equivalence avec l'axiome du choix
Nous avons précedemment évoqué l'équivalence du théorème de Tychonov avec l'axiome du choix. Cette équivalence, bien qu'a priori surprenante, se comprend mieux en remarquant que l'on peut définir une topologie sur un ensemble quelconque. En l'occurrence, nous allons utiliser une légère variante de la topologie cofinie, qui possède une propriété très intéressante: tout espace est compact pour la topologie cofinie.
Soit donc
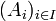 une famille d'ensemble, nous voulons montrer
une famille d'ensemble, nous voulons montrer 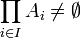 . On suppose, quitte à réindexer par un ensemble I' que
. On suppose, quitte à réindexer par un ensemble I' que 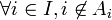 . Alors, on pose
. Alors, on pose 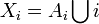 , et on munit Xi de la topologie τi formée de l'ensemble vide, de tous les ensembles de complémentaire fini, et du singleton {i} (On vérifiera qu'on a alors bien une topologie, et que Xi est alors compact). Par Tychonov, le produit X des Xi est compact.
, et on munit Xi de la topologie τi formée de l'ensemble vide, de tous les ensembles de complémentaire fini, et du singleton {i} (On vérifiera qu'on a alors bien une topologie, et que Xi est alors compact). Par Tychonov, le produit X des Xi est compact.On remarque que, en notant pi la projection sur Xi, on a:
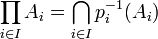 . Or X est compact: pour montrer que
. Or X est compact: pour montrer que 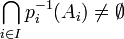 on va se servir de la contraposée de la propriété de Borel-Lebesgue pour les fermés: si chaque
on va se servir de la contraposée de la propriété de Borel-Lebesgue pour les fermés: si chaque 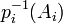 est fermé et que toute intersection finie de
est fermé et que toute intersection finie de 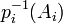 est non vide, alors l'intersection des
est non vide, alors l'intersection des 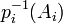 est non vide, ce qui achèvera la preuve.
est non vide, ce qui achèvera la preuve.Or
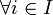 comme Ai est le complémentaire de {i} ouvert, Ai est fermé. Donc par continuité de la projection pi,
comme Ai est le complémentaire de {i} ouvert, Ai est fermé. Donc par continuité de la projection pi, 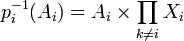 est fermé. De plus soit
est fermé. De plus soit 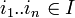 , alors
, alors 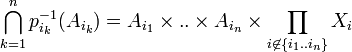 qui est non vide: en effet en choisissant a1..an éléments respectifs de A1..An on peut définir
qui est non vide: en effet en choisissant a1..an éléments respectifs de A1..An on peut définir 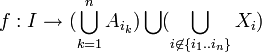 par f(i1) = a1..f(in) = an et f(i) = i si
par f(i1) = a1..f(in) = an et f(i) = i si 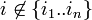 : on a donc bien la propriété annoncée.
: on a donc bien la propriété annoncée.Notes
Voir aussi
- Théorème de Tychonov dans les ensembles flous
- Portail des mathématiques
Catégories : Théorème de mathématiques | Compacité
Wikimedia Foundation. 2010.
