Weierstrass

Karl Weierstrass

Karl Theodor Wilhelm Weierstrass
Naissance	31 octobre 1815 Ostenfelde (Westphalie)
Décès	19 février 1897 Berlin (Allemagne)
Nationalité	Allemagne
Champs	mathématicien
Institution	Université technique de Berlin
Diplômé	université de Münster
Célèbre pour	analyse, fonction elliptique
Distinctions	médaille Copley (1895)
modifier

Karl Theodor Wilhelm Weierstrass, habituellement appelé Karl Weierstrass, né le 31 octobre 1815 à Ostenfelde (Westphalie), mort le 19 février 1897 à Berlin, était un mathématicien allemand, lauréat de la médaille Copley en 1895. Il a étudié les mathématiques à l'université de Münster et obtint une chaire à l'Université technique de Berlin. Il fut immobile les trois dernières années de sa vie et s'étint à Berlin à la suite d'une pneumonie.

Il créa avec Alfred Enneper (1830-1885) une classe complète de paramétrisations.

Karl Weierstrass est souvent cité comme le « père de l'analyse moderne ». Il consolida des travaux de Cauchy (1789-1857) sur les nombres irrationnels et leur amena une nouvelle compréhension. Ses travaux les plus connus portent sur les fonctions elliptiques.

C'est lui qui le premier rendit public un exemple de fonction continue nulle part dérivable.

Sommaire 1 Étudiants de Karl Weierstrass 2 Contributions mathématiques 2.1 Fiabilité ("soundness") de l'analyse 2.2 Fonction de Weierstrass 2.3 Calcul des variations 3 Voir aussi 4 Notes et références 4.1 Liens externes

Étudiants de Karl Weierstrass

• Sofia Kovalevskaïa
• Georg Cantor

Contributions mathématiques

Fiabilité ("soundness") de l'analyse

Weierstrass étudia la fiabilité ("soundness") de l'analyse. À cette époque, les démonstrations de l'analyse s'appuyaient sur des définitions ambiguës, d'où la nécessité de nouvelles définitions. Tandis que Bolzano avait développé une définition suffisamment rigoureuse des limites dès 1817 (et peut-être même auparavant), ses travaux restèrent quasi inconnus de la communauté mathématique pendant des années, et d'autres mathématiciens éminents, comme Cauchy, n'avaient que de vagues définitions de la limite et de la continuité d'une fonction. Weierstrass définit la continuité comme suit :

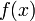est continue en 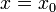si pour tout 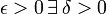tel que

Weierstrass formula également une définition de la limite et de la dérivée «en (ε, δ)», telle qu'on l'enseigne aujourd'hui.

Avec ces nouvelles définitions, il put donner des démonstrations rigoureuses de plusieurs théorèmes qui reposent sur des propriétés des nombres réels jusqu'alors tenues pour intuitives, tels le théorème des valeurs intermédiaires, le théorème de Bolzano-Weierstrass et le théorème de Borel-Lebesgue.

Fonction de Weierstrass

Le 18 juillet 1872, Weierstrass exposa à l'Académie royale des sciences de Berlin l'exemple d'une fonction continue partout et dérivable nulle part, appelée aujourd'hui fonction de Weierstrass, qu'il enseignait dans ses cours depuis 1861. Il causa ainsi une grande surprise dans le monde mathématique: on croyait d'ordinaire qu'une fonction continue en tout point est nécessairement dérivable sauf peut-être en quelques points. (En fait, on trouve dans le manuscrit Functionenlehre de Bernard Bolzano, rédigé avant 1834, un autre exemple, mais il fut seulement exposé en 1921 et publié en 1930^[1].)

Calcul des variations

Weierstrass fit aussi de avancées significatives dans le champ du calcul des variations. En utilisant les outils de l'analyse qu'il avait aidé à développer, Weierstrass put reformuler complètement la théorie, ce qui ouvrit la voie à l'étude moderne du calcul des variations. Weierstrass établit par exemple une condition nécessaire à l'existence d'un extrémum global de problèmes variationnels. Il contribua à l'expression de la condition Weierstrass-Erdmann, qui donne les conditions suffisantes pour qu'un extrémum ait un coin.

Voir aussi

• Fonctions elliptiques de Weierstrass
• Équation de Weierstrass
• Théorème de Stone-Weierstrass
• Théorème de Bolzano-Weierstrass
• Théorème de Weierstrass-Casorati
• Théorème de factorisation de Weierstrass
• Fonction de Weierstrass
• Théorème de Lindemann-Weierstrass

Notes et références

Liens externes

• comme Biographie de Karl Weierstrass

• Portail des mathématiques