Theoreme isoperimetrique

Theoreme isoperimetrique

Théorème isopérimétrique

En géométrie, un théorème isopérimétrique traite d'une question concernant les compacts d'un espace métrique muni d'une mesure. Un exemple simple est donné par les compacts d'un plan euclidien. Les compacts concernés sont ceux de mesures finies ayant une frontière aussi de mesure finie. Dans l'exemple choisi, les compacts concernés sont ceux dont la frontière est une courbe rectifiable, c'est-à-dire essentiellement non fractale. Les mesures du compact et de sa frontière sont naturellement différentes, dans l'exemple choisi, la mesure du compact est celle d'une surface, celle de la frontière, une longueur.

Un théorème isopérimétrique caractérise les compacts ayant la mesure la plus grande possible pour une mesure de leur frontière fixée. Dans le plan euclidien et si la mesure est celle de Lebesgue, un théorème isopérimétrique indique qu'un tel compact est un disque. En dimension 3, toujours avec une géométrie euclidienne, une autre version du théorème indique que c'est une sphère. D'une manière plus générale, dans un espace euclidien de dimension n, muni de la mesure de Lebesgue, l'optimum est obtenu par une sphère, ce qui donne l'inégalité isopérimétrique suivante, si K est un compact et B la boule unité :

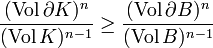
\frac{(\text{Vol}\,\partial K)^n}{(\text{Vol}\, K)^{n-1}} \ge \frac{( \text{Vol}\,\partial B) ^n } { (\text{Vol}\, B) ^{n-1} }

Un autre exemple de résultat est obtenu si le choix de la mesure est celui du nombre de points d'un réseau inclus dans le solide K, et si les compacts choisis sont des polytopes convexes à sommets entiers. En dimension 2 si le réseau est Z2, on trouve le théorème de Pick, indiquant que la mesure du polytope P (c'est-à-dire le nombre de points de Z2 qu'il contient) est égale à sa surface plus la moitié des points que contient sa surface plus un.

Un théorème isopérimétrique est souvent difficile à établir. Même un cas simple, comme celui du plan euclidien muni de la mesure de Lebesgue, est relativement technique à démontrer. Une des méthodes partielles de preuve, connue depuis la démonstration de Hurwitz en 1901 est d'utiliser un résultat d'analyse, issu de la théorie des séries de Fourier, connu sous le nom d'inégalité de Wirtinger. Le résultat reste partiel car il ne traite que des surfaces dont la frontière est une courbe de classe C1.

Les théorèmes isopérimétriques sont actuellement l'objet d'une intense recherche en mathématiques, en particulier en analyse fonctionnelle et en théorie des probabilité, suite à leurs liens étroits avec les phénomènes de concentration de la mesure.

Une approche plus élémentaire est proposée dans l'article Isopérimétrie.

Sommaire

Fragments d'histoire

Prémisses

La connaissance de théorème isopérimétrique est ancienne, près de 3 000 ans[1]. Le résultat essentiel de l'époque est l'œuvre de Zénodore IIe siècle av. J.-C. qui démontre un résultat que l'on exprimerait maintenant de la manière suivante : S'il existe un polygone à n cotés de surface maximale à périmètre donné, alors il est régulier[2]. Cette partie de l'histoire est traitée dans l'article Isopérimétrie. Les études des théorème isopérimétriques datant de l'antiquité se fonde exclusivement sur la géométrie du triangle. Ces méthodes, assez élémentaires, ne permettent pas d'aller beaucoup plus loin. Par exemple, démontrer l'existence d'une solution est hors de portée. Il faut attendre près de 2 000 ans pour que l'étude de cette question soit enrichie à l'aide d'apports théoriques de nature différente.

Jacques Bernoulli (1654-1705) étudie la question pour répondre à des questions de mécanique statique et plus précisément s'intéresse à la forme que doit posséder une poutre pour offrir le maximum de résistance possible, la résolution d'une telle question débouche sur un théorème isopérimétrique, le demi-cercle est parfois la forme offrant la meilleure résistance. Si Bernoulli ne parvient pas à finaliser un résultat, il utilise de nouveaux outils issus du calcul différentiel. Le mariage de la géométrie de l'analyse est promis à un grand avenir, même si un théorème isopérimétrique n'est pas encore accessible.

Le XIXe siècle est celui des progrès majeurs. La première avancée est le fruit du travail de Jakob Steiner (1796-1863). Il montre que, si une solution existe, elle est nécessairement unique et c'est le disque. Pour cela, il développe un outil, maintenant appelé symétrisation de Steiner[3] et encore utilisé pour établir des théorèmes d'isopérimétrie. Son idée majeure consiste à remarquer que, si l'on coupe une solution à l'aide d'une droite en deux parties de surfaces égales, il est possible de construire une nouvelle surface optimale à l'aide de la duplication d'une des deux parties. Sa démonstration est présentée dans l'article Isopérimétrie.

Calcul variationnel

Pour l'obtention d'une preuve complète, au moins en dimension 2, une difficulté majeure n'est toujours pas franchie, celle de la preuve de l'existence d'une solution. Les premiers éléments de réponse proviennent de la démarche initiée par Bernoulli. Une hypothèse supplémentaire, un peu étrange, est supposée : la frontière de la surface est lisse. L'étrangeté provient du fait qu'une ondulation sur la surface a tendance à plus augmenter le périmètre que l'aire. Plus la courbe frontière est irrégulière, plus elle est loin de l'optimale, mais plus la démonstration devient difficile[4]. Karl Weierstrass (1815-1897) formalise le calcul des variations et établit les bases de l'analyse fonctionnelle. Cette approche consiste à étudier non pas une courbe spécifique, mais un ensemble de courbes qui varient, par exemple à l'aide d'un paramètre. En faisant varier ces courbes, on montre que le cercle est l'optimum recherché[5]. Au moins pour la dimension 2, une fois l'existence d'un optimum établi pour les surfaces à la frontière régulière, il n'est plus trop difficile de montrer le théorème général, on sait en effet approximer une courbe fermée continue par une autre continument dérivable.

La généralisation aux dimensions supérieures est naturelle. Dans un premier temps, on suppose l'existence d'une solution au théorème et on montre que cette solution est nécessairement une sphère de dimension n. Le raisonnement est très physique, c'est celui qui détermine la forme d'une bulle de savon. L'équilibre de la bulle est le fruit de deux forces qui s'annulent : la pression due à l'aire enfermée dans la bulle et la tension superficielle de la surface. Un rapide calcul de variation montre que la courbure moyenne de la sphère est nécessairement constante. En 1900, on sait que le seul compact strictement convexe de courbure moyenne constante est une sphère[6]. Une fois encore, la démonstration de l'existence d'une solution s'avère la partie délicate. Une première démonstration en dimension 3 est l'œuvre H. A. Schwarz en 1890[7].[8]

Géométrie des convexes

Si la démarche fondée sur le calcul variationnel débouche, la généralisation à des dimensions supérieures n'est pas aisée. Une autre approche, issue de la théorie algébrique des nombres est finalement plus prometteuse. Hermann Minkowski (1864-1909) développe une approche géométrique qui l'amène à étudier le nombre de points à coordonnées entières que contiennent certains convexes, problème proche de l'isopérimétrie. La fonction qui associe à un convexe compact de Rn, le cardinal de son intersection avec le réseau Zn est une mesure. Le théorème de Minkowski, qui procède de cette logique, permet d'élucider de manière élégante la structure du groupe des classes d'idéaux. Une nouvelle structure géométrique est étudiée ; au lieu de considérer une géométrie euclidienne de dimension n, Minkowski étudie un ensemble dont les points sont des compacts convexes. Cet ensemble est muni d'une addition.

Felix Hausdorff (1868-1942) trouve une distance naturelle pour un espace un peu plus vaste, celui des compacts. La topologie associée à cette distance est bien adaptée. Les fonctions volumes et surfaces, qui associent à un convexe compact sa mesure et la mesure de sa frontières sont continues. Il en est de même pour la somme de Minkwoski. Enfin, l'espace est complet ainsi que le sous-ensemble des convexes. Enfin les polytopes forment un ensemble dense.

En dimension 2, l'étude de la somme de Minkwoski et de la sphère de rayon t et de centre le vecteur nul avec un convexe compact donne l'expression polynomiale a + pt + πt2, où a désigne l'aire du convexe et p son périmètre. Démontrer le théorème isopérimétrique en dimension 2 revient à montrer que p2 est plus grand que 4πa, ce qui revient à dire que l'expression polynomiale précédente admet des racines réelles, ce que fait Minkowski[9]. T. Bonnesen va plus loin, en 1921 il démontre que si r est le rayon d'un cercle inscrit et R le rayon d'un cercle circonscrit, on dispose de la majoration suivante[10] :

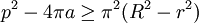
p^2 - 4\pi a \ge \pi^2(R^2 -r^2) \;

Autrement dit, l'égalité ne peut avoir lieu que si le convexe est un disque. Cette démarche peut être généralisée aux dimensions supérieures. A. Aleksandrov et W. Fenchel utilisent cette démarche pour établir le théorème isopérimétrique général, pour les géométries euclidiennes et la mesure de Lebesgue[11] en 1937.[12]

Plan euclidien

Dans tout le paragraphe, S désigne une surface fermée convexe d'un plan euclidien dont l'aire, noté a, est finie et strictement positive ; le périmètre l'est aussi et est noté p.

Dans le plan euclidien, le théorème isopérimétrique prend la forme suivante :

  • La surface S possède une aire supérieure à celle d'un disque de périmètre p. L'égalité entre les aires n'a lieu que si S est un disque.

Ce théorème est souvent exprimé sous une forme équivalente, dite inégalité isopérimétrique :

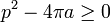
p^2 - 4\pi a \ge 0\;

Aucune hypothèse n'est nécessaire sur la nature de la surface. Cependant, si elle n'est pas suffisamment régulière, le périmètre n'est pas fini, l'inégalité ne possède alors aucun intérêt.

Démonstrations géométriques élémentaires

En dimension 2, on dispose d'une propriété qui simplifie grandement les choses :

  • Si une surface n'est pas convexe mais est d'aire et de périmètre fini, il existe une surface S de périmètre strictement plus petit et d'aire strictement plus grand.

Intuitivement, ce théorème est relativement évident. L'enveloppe convexe de S possède une aire strictement plus grande et un périmètre strictement plus petit que S, si l'ensemble n'est pas convexe. Pour cette raison, il est pertinent de ne s'intéresser qu'aux surfaces convexes. Comme l'aire et le périmètre, s'ils existent, d'un convexe est le même que celui de son adhérence, se limiter aux convexes fermés ne réduit en rien la généralité des solutions trouvées. Enfin, comme toute surface de périmètre fini est bornée, si elle est fermée, elle est nécessairement compacte (cf. l'article Topologie d'un espace vectoriel de dimension finie).

L'article Isopérimétrie établit encore deux résultats à l'aide de la géométrie du triangle :

  • Si un polygone à n sommets possède une aire maximale pour un périmètre donné, ce polygone est régulier.
  • Si une surface possède une aire maximale pour un périmètre donné, alors cette surface est celle d'un disque.

La partie plus difficile à établir est l'existence de telles surfaces.

Calcul des variations

Une première manière de simplifier la question est du supposer que la frontière est suffisamment régulière. En 1904, Hurwitz propose une démonstration particulièrement élégante[13], qui se fonde sur l'inégalité de Wirtinger :

  • Soit une courbe fermée définie par une fonction f(t)=(x(t),y(t)) périodique, continûment dérivable définissant une surface S. La majoration suivante est vérifiée, l'égalité n'ayant lieu que si la courbe définit un cercle.
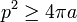
p^2\geq 4\pi a\;

Le prix à payer contre l'élégance et la simplicité est le caractère partiel de la solution. L'existence d'une solution optimale est bien démontrée, mais uniquement si la frontière est lisse. Or la frontière peut être quelconque. Évidemment, si elle n'est pas finie, la formule est vraie mais possède peu d'intérêt.[14]

Démonstration
  • Inégalité de Wirtinger :

Soit f une fonction 2π-périodique, de moyenne nulle, de classe C1 par morceaux et continue. Alors

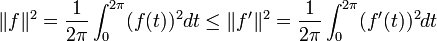
\|f\|^2 = \frac1{2\pi}\int_{0}^{2\pi} (f(t))^2 dt \leq \|f'\|^2 = \frac1{2\pi}\int_{0}^{2\pi} (f'(t))^2 dt\;

De plus si ||f||=||f'||, alors f est une fonction sinusoïdale

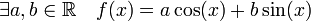
\exists a, b \in \mathbb R \quad f(x)=a\cos(x)+b\sin(x)

On trouve une démonstration dans l'article inégalité de Wirtinger.

  • Aucune surface dont la frontière est une courbe fermée de classe C1 par morceaux ne possède une aire strictement supérieure à celle du disque de même périmètre :

Comme f définit une courbe fermée, c'est-à-dire une boucle, on peut considérer cette courbe comme une fonction périodique, parcourant une infinité de fois la boucle. Soit T cette période. Comme une translation est une isométrie, elle ne modifie ni le périmètre p ni l'aire a de la surface délimitée par f. On peut donc supposer que le centre de gravité de la surface S est le centre du repère orthonormal utilisé.

Déterminons dans un premier temps le périmètre p. Il est égal à l'intégrale de la norme de la vitesse sur une période ; on obtient la formule :

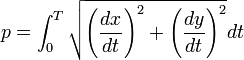
p= \int_0^T \sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2} d t

Si l'on choisit comme paramètre l'abscisse curviligne s, c'est-à-dire que l'arc est parcouru à vitesse uniforme p/2π. la valeur T est égale à 2π avec ce nouveau paramétrage.

Déterminons ensuite la valeur de l'aire a. Elle est définie par la formule, exprimée de plusieurs manières différentes :

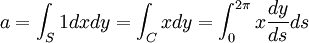
a = \int_S 1 dxdy = \int_C xdy =\int_0^{2\pi} x\frac{dy}{ds}ds
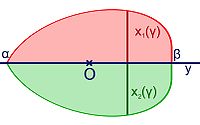
Problème isopérimétrique Steiner (4).jpg

Pour s'en rendre compte, on peut soit utiliser le puissant théorème de Stokes sur la courbe C associée à la fonction f, soit remarquer que S est convexe. Si α est la plus petite valeur atteinte par y(t) , β la plus grande et γ une valeur entre les deux, il existe deux points de la courbe ayant pour ordonnées γ, que l'on peut noter x1(γ) et x2(γ). Les fonctions x1 et x2 de [α, β] dans R sont toutes deux continues et correspondent à l'illustration de la figure de droite. Par définition de a, sa valeur est égale à la somme des aires en rouge et vert sur la figure :

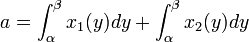
a = \int_{\alpha}^\beta x_1(y)dy + \int_{\alpha}^\beta x_2(y)dy

En utilisant la variable s curviligne au lieu de y, on remarque qu'il existe deux valeurs v1 et v2 de l'intervalle [0, p] tel que :

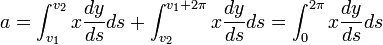
a = \int_{v_1}^{v_2} x\frac {dy}{ds}ds + \int_{v_2}^{v_1+ {2\pi}} x\frac {dy}{ds}ds = \int_0^{2\pi} x\frac {dy}{ds}ds

Il est temps d'évaluer p2 - 4π.a :

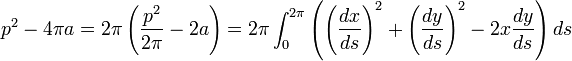
p^2-4\pi a = 2\pi \left(\frac {p^2}{2\pi} -2a\right) = 2\pi\int_0^{2\pi} \left(\left(\frac {dx}{ds}\right)^2+\left(\frac{dy}{ds}\right)^2-2x\frac {dy}{ds}\right)ds

Comme x vérifie les hypothèses de l'inégalité de Wirtinger :

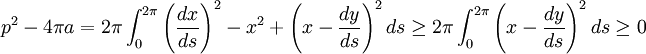
p^2-4\pi a = 2\pi \int_0^{2\pi} \left(\frac {dx}{ds}\right)^2 - x^2 + \left(x-\frac {dy}{ds}\right)^2 ds \ge 2\pi\int_0^{2\pi} \left(x-\frac {dy}{ds}\right)^2 ds\ge 0
  • L'égalité est atteinte si, et seulement si, la surface est un disque :

Pour le cas d'égalité : d'une part il faut qu'il y ait égalité dans l'inégalité de Wirtinger, ce qui donne l'expression de x(s). D'autre part pour que cette intégrale s'annule, on doit avoir y'(s)=x(s). Ces deux conditions donnent bien un cercle de rayon 1, paramétré à vitesse uniforme. Et bien sûr tous les cercles sont solutions, quelle que soit la façon de les paramétrer car leur aire est égale à π.r2 et leur périmètre à 2π.r, si r désigne le rayon.

 

Polygone et Steiner

La fonction associe à un triangle de périmètre égal à 3, son aire.

Les démonstrations historiques ont toutes un chainon manquant. Elles montrent qu'une surface, polygonale ou quelconque, qui ne possède pas la bonne propriété : être régulier ou être un disque, n'est pas un optimum. En revanche, elle ne montre pas qu'un tel optimum existe. Une fois l'existence d'un tel optimum démontrée, on sait alors qu'il est unique et l'on connait sa géométrie. Mais la démonstration de cette existence est l'élément qui bloque les démonstrations pendant de si nombreux siècles. Elle demande une compréhension d'un aspect alors mal maitrisé de la géométrie : la topologie.

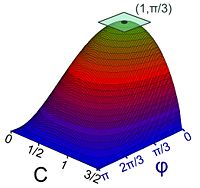
Les preuves actuelles procèdent d'une démarche encore inconnue à l'époque de Steiner. La géométrie étudiée n'est plus le plan euclidien, support de la surface étudiée, mais un univers où chaque point est une surface. Elle est illustrée sur la figure de gauche dans le cas particulier des triangles. La fonction considérée est celle qui, à un triangle de périmètre 3, associe son aire. Le triangle est représenté par deux paramètres, c la longueur d'une arête et φ l'angle entre deux arêtes dont celle de longueur c. Si l'angle est de mesure nulle ou égale à π, l'aire est nulle, il en est de même si c est égal à 0 ou à 3/2. La représentation graphique montre que le maximum est bien atteint. Dans ce cas particulier, le sommet est le triangle décrit par le couple (1, π/3).

Dans le cas des polygones à n sommets, où n est un entier supérieur à 2, la configuration est relativement simple. On identifie un polygone à un vecteur de R2n. L'ensemble des polygones devient une partie d'un espace vectoriel euclidien, cette fois-ci, de dimension 2n. La topologie d'un espace euclidien dispose d'une propriété adéquate. Un théorème assure que les ensembles fermés et bornés sont des compacts. La fonction, qui à un polygone associe son aire est continue. Un des charmes des compacts est que toute fonction continue, définie sur un compact et à valeur dans R atteint ses bornes. La configuration est analogue à celle de la figure de gauche. Ce qui permet d'établir le chainon manquant :

  • Il existe un polygone à n cotés et de périmètre p qui possède une aire maximale.

Pour le cas général, une démarche analogue à la précédente ne permet pas de conclure. En se limitant aux convexes compacts, la zone qui nous intéresse est bien un fermé borné, mais la dimension de l'espace est ici infinie. Or si la dimension n'est pas finie, le théorème de Riesz montre qu'un fermé borné comme la boule unité n'est jamais compact. De plus, la fonction périmètre n'est plus continue, on peut approcher de plus en plus précisément un disque de rayon 1 par des carrés de plus en plus petits, l'approximation garde un périmètre égal à 8 sans s'approcher de la valeur 2π, même si elle devient excellente.

En revanche, il est possible d'approcher précisément la frontière d'un convexe compact par un polygone de périmètre plus petit et de surface presque égale à celle du convexe. Cette propriété, et le fait d'avoir établi le théorème isopérimétrique pour les polygones, permet aisément de montrer qu'aucune surface de périmètre p ne peut posséder une aire supérieure à celle d'un disque de même périmètre. Le disque est ainsi un des optimums recherchés, et les travaux de Steiner montrent que cet optimum est unique.

  • Toute surface S possède une aire plus petite que celle du disque de même périmètre. L'égalité n'a lieu que si la surface S est elle aussi un disque.
Démonstrations
  • Il existe un polygone à n cotés et de périmètre p qui possède une aire maximale :

On munit le plan d'un repère orthonormal, et on considère l'application, qui à un polygone convexe à n sommets, associe dans R2n la suite des coordonnées de ses sommets. Ici R désigne l'ensemble des nombres réels et R2n l'espace vectoriel canonique de dimension 2n. Réciproquement à tout élément u de R2n, on associe l'enveloppe convexe des points ayant comme suite de cordonnées u. On obtient une application de R2n dans l'ensemble des polygones ayant un nombre de sommets inférieur ou égal à n. Cette application n'est pas injective, mais est surjective.

Soit φ la fonction de R2n dans R2, qui associe à un vecteur u le barycentre des n vecteurs dont u est la suite des coordonnées. La fonction φ est continue, l'image réciproque du vecteur nul est un fermé de R2n, que l'on note F1. On ne cherche que des solutions dans ce fermé, ce qui n'est pas contraignant. En effet, si un polygone P est une solution quelconque du problème isopérimétrique, la translation de P par l'inverse de son barycentre est une solution dans F1. Comme la translation est une isométrie, les propriétés géométriques de l'image par la translation sont les mêmes que celle de P.

Soit ψ l'application de R2n dans R qui associe à un vecteur u le périmètre du polygone associé à u. Cette application est encore continue et l'image réciproque du nombre réel p est encore un fermé F2 de R2n. L'intersection C de F1 et de F2 est fermé, car intersection de deux fermés. Cet ensemble est aussi borné. Un vecteur est dans F1 seulement si l'enveloppe convexe des vecteurs de dimension 2 contient le vecteur nul. Le segment allant du vecteur nul à un l'un des vecteurs de dimension 2 possède une longueur inférieure à la moitié du périmètre de l'enveloppe convexe. Un élément de C ne possède donc aucune coordonnée supérieure à la moitié de p. L'ensemble C possède les bonnes propriétés pour conclure. Si une solution au problème isopérimétrique posé existe, on en trouve nécessairement au moins une dans C. De plus, C est un fermé borné, or dans un espace vectoriel de dimension finie, comme R2n, les fermés bornés sont des compacts.

On considère l'application ξ de R2n dans R, qui à un vecteur u associe la surface de son polygone. Cette application est définie et continue sur le compact C. L'image de C par ξ est un compact, la borne supérieure de cet ensemble est atteinte car tout compact de R contient sa borne supérieure. L'enveloppe convexe d'un vecteur u ayant pour image par ξ cette borne supérieure, est un polygone ayant au plus n cotés, de périmètre p et de surface maximale. C'est une solution au problème isopérimétrique posé.

  • Il n'existe aucune surface d'aire supérieure à celle d'un disque de même périmètre :
Problème isopérimétrique Steiner (5).jpg

On raisonne par l'absurde. Quitte à effectuer une homothétie, on suppose qu'il existe une surface S de périmètre égal à 2π et d'aire égal à π + A, où A est un nombre réel strictement positif. On suppose que S est convexe, sinon, il est toujours possible de choisir son enveloppe convexe de périmètre plus petit et d'aire plus grande.

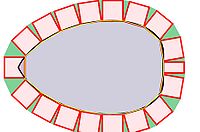
On construit un polygone de périmètre plus petit que 2π et d'aire supérieure à π + A/2. La démonstration précédente montre qu'un tel polygone n'existe pas, ce qui démontre que la surface S ne peut pas plus exister et constitue l'absurdité recherchée. Ce polygone est illustré sur la figure de droite. Soit ε un nombre réel strictement positif plus petit que 1 et que le rapport de A/6π. Enfin, soit P le polygone dont les sommets sont des points de la frontière de S, régulièrement espacés à une distance ε l'un de l'autre. Le polygone correspond à la figure constituée par les bases des carrés rouges. Il existe peut-être une arête du polygone de longueur inférieure à ε, celle la plus à droite sur la figure.

On considère l'enveloppe E constituée des points à une distance inférieure ou égale à ε de P. Cette enveloppe est l'union de l'intérieur du polygone P, en bleu, des carrés rouges d'arêtes de longueur ε et de portions d'un disque de rayon ε, en vert sur la figure. L'union des portions vertes forme un disque complet. L'aire ae de l'enveloppe E est la somme des aires de ces différentes surfaces. Si pp désigne le périmètre du polygone, on obtient :

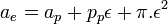
a_e = a_p + p_p\epsilon + \pi.\epsilon^2 \;

Le périmètre du polygone est par construction plus petit que celui de la surface S, qui est égale à 2π, on en déduit :

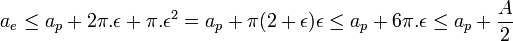
a_e \le a_p + 2\pi.\epsilon + \pi.\epsilon^2 = a_p + \pi(2 + \epsilon)\epsilon \le a_p + 6\pi.\epsilon \le a_p + \frac A2

Un petit lemme, démontré ci-dessous, montre que l'enveloppe E contient la surface S. L'aire de S, c'est-à-dire π + A est en conséquence plus petite que celle de ae :

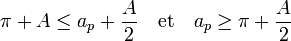
\pi + A \le a_p + \frac A2 \quad \text{et}\quad a_p \ge \pi + \frac A2

On a bien construit un polygone d'aire strictement supérieure à π et de périmètre strictement inférieur à 2π. Or aucun polygone de même périmètre qu'un disque ne possède une aire supérieure à celle du disque : ce résultat est absurde. Cette absurdité montre qu'une surface S d'aire strictement supérieure à celle d'un disque de même périmètre ne peut exister.

  • Toute surface S possède une aire plus petite que celle du disque de même périmètre. L'égalité n'a lieu que si la surface S est elle aussi un disque :

Il ne reste plus qu'à étudier le cas de l'égalité. La preuve précédente montre qu'il existe bien au moins une surface d'aire optimale pour un périmètre donné, le disque. La démonstration de Steiner montre que, si une telle surface existe, elle est nécessairement un disque.

  • L'enveloppe E contient la surface S :
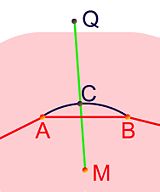
Problème isopérimétrique Steiner (6).jpg

On raisonne par l'absurde et on suppose l'existence d'un point Q de S qui ne soit pas élément de E. La figure illustrative est à droite, la surface E est celle sur fond rouge. La convexité de S met en évidence une absurdité. On utilise un théorème indiquant qu'il existe une droite d'appui pour chaque point de la frontière d'un convexe. C'est-à-dire une droite passant par le point frontière et séparant le plan en deux demi-plans dont l'un est fermé. Ce demi-plan fermé contient l'intégralité du convexe.

Soit M un point de l'intérieur du polygone P. On considère le segment d'extrémité Q et M. Ce segment croise la frontière du polygone et il existe une arête AB dont l'intersection avec le segment QM est non vide. Ce point d'intersection ne peut être un sommet. En effet, si ce point est un sommet, par exemple A, comme A est aussi un point frontière de S, il possède une droite d'appui, qui est nécessairement celle passant par Q et M car ces deux points sont élément de S. Or un voisinage de M est contenu dans l'intérieur du polygone et donc dans celui de S, ce voisinage contient des points de chaque coté de la droite, ce qui est impossible.

Considérons la frontière du convexe S entre A et B, en bleu sur la figure ; elle traverse la droite QM. Soit C le point d'intersection, par construction du polygone P, le point C est à une distance inférieure à ε de A et se trouve dans E, à la différence de P qui n'est pas élément de E, ces deux points sont donc différents. Le point C est un point frontière du convexe S, il possède une droite d'appui. Le même argument que celui utilisé précédemment montre que cette droite d'appui est nécessairement celle passant par Q et M. Or, on a vu qu'une telle droite ne peut être une droite d'appui.

 

Somme de Minkowski

Article détaillé : Somme de Minkowski.
Somme de Minkowski d'un hexagone de rayon 1 et de la boule unité

On pourrait croire que les deux démonstrations précédentes closent le débat du problème isopérimétrique du plan euclidien E. Il n'en est rien. La démarche d'Hurwitz n'apporte aucune information si la frontière n'est pas suffisamment lisse. Celle présentée au dernier paragraphe se généralise mal aux dimensions supérieures. A partir de la dimension 3, il ne faut plus espérer trouver des polyèdres convexes réguliers, encore appelés solides de Platon approchant avec la précision voulue la sphère. Il n'existe que 5 solides de ce type.

Hausdorff et Minkowski développent une autre approche, fondée sur une géométrie un peu différente. Ici, le terme de géométrie désigne l'étude d'un ensemble muni d'une distance et d'une opération algébrique compatible. L'espace considéré est celui des compacts non vides, la distance celle de Hausdorff et l'opération est la somme de Minkowski, dont la compatibilité avec la distance se traduit par la continuité de l'opération. La somme de Minkowski P + Q correspond à l'ensemble des sommes dont le premier membre est élément de P et le second de Q :

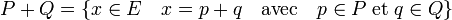
P + Q = \{x \in E\quad x = p + q \quad\text{avec}\quad p \in P \;\text{et}\; q \in Q\}

Si S désigne un convexe compact non vide et t.B la boule fermée de centre le vecteur nul et de rayon t, l'aire de la somme S + t.B prend la forme suivante, connue sous le nom de formule de Steiner-Minkowski :[15]

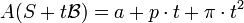
A(S + t\mathcal B) = a + p\cdot t + \pi \cdot t^2 \;

Ici, a désigne l'aire de S et p son périmètre. Cette somme est illustrée sur la figure de gauche dans le cas d'un hexagone. La somme correspond à l'ensemble des points du plan à une distance inférieure ou égale à t de S. Appliquer à l'hexagone jaune de la figure de gauche, on peut décomposer cette somme en trois régions. La première correspond à la figure initiale S en jaune, la deuxième aux points situés sur un rectangle de coté une arête du polygone et de largeur t, correspondant aux 6 rectangles bleus. L'aire des surfaces bleues est égale à p.t. Enfin, à chaque sommet est associée une portion de disque de rayon t, en vert sur la figure. L'union de ces portions de disque forme un disque complet, d'où le dernier terme de la formule. La démonstration dans le cas non polygonal est donnée dans l'article détaillé.

La surface s'exprime comme un polynôme de degré 2, son discriminant est égal à p2 - 4π.a. On reconnait là le terme de l'inégalité isopérimétrique. Démontrer le théorème revient à dire que le discriminant n'est jamais négatif, ou encore que le polynôme admet au moins une racine. Ce résultat s'obtient directement comme une conséquence de l'inégalité de Brunn-Minkowski.

Démonstration

L'inégalité de Brunn-Minkowski montre que :

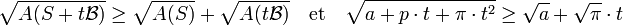
\sqrt {A(S + t\mathcal B)} \ge \sqrt{A(S)} + \sqrt{A(t\mathcal B)}\quad\text{et}\quad \sqrt{a + p\cdot t + \pi \cdot t^2} \ge \sqrt a + \sqrt \pi \cdot t

Au carré, cette majoration devient :

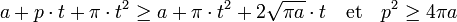
a + p\cdot t + \pi \cdot t^2 \ge a + \pi \cdot t^2 + 2\sqrt {\pi a} \cdot t \quad\text{et} \quad p^2 \ge 4\pi a
 

Inégalité de Bonnesen

L'opposé rayon du cercle inscrit ainsi que celui du cercle circonscrit se trouvent entre les racines du polynôme.

A y regarder de près, le paragraphe précédent propose bien une méthode généralisable pour montrer l'inégalité isopérimétrique, mais elle n'indique pas comment traiter le cas de l'égalité. Plus précisément, la démonstration n'indique pas que seul le cercle est la solution, partie difficile de la démonstration qui a bloqué tant de monde depuis l'Antiquité.

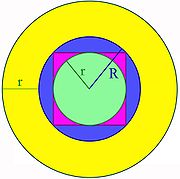
Il existe bien une preuve, donnée dans l'article isopérimétrie et fondée sur une symétrisation de Steiner. Elle est mal commode à généraliser en dimension quelconque. Bonnesen trouve une expression simple, en fonction d'un cercle inscrit et d'un circonscrit. Le cercle est dit inscrit dans un compact S s'il est inclus dans S et si son rayon r est maximal. Un cercle est dit circonscrit dans S s'il contient S et si son rayon R est minimal. L'inégalité de Bonnesen s'exprime de la manière suivante, si a est l'aire du compact et p son périmètre[16] :

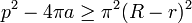
p^2 - 4\pi a \ge \pi^2(R - r)^2\;

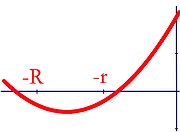
Ce résultat signifie que le discriminant du polynôme du second degré, qui à t associe l'aire de la surface S + t.B admet deux racines distinctes si un cercle inscrit possède un rayon strictement plus petit qu'un cercle circonscrit. Autrement dit, pour le l'égalité isopérimétrique ait lieu, il est nécessaire que les deux rayons soient égaux, ce qui ne peut arriver que pour le cercle. Un autre résultat, un peu plus fort indique que les deux valeurs -R et -r se situent entre les deux racines, comme illustré sur la figure de droite. De la même manière, on en déduit la nécessité de l'égalité entre R et r pour atteindre l'optimal.

Démonstration
  • La valeur -r est d'image négative par le polynôme qui, à t associe l'aire de la surface S + t.B :
Inégalité de Bonnesen (2).jpg

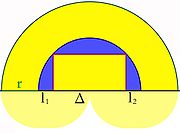
On considère un compact convexe non vide S, un cercle inscrit, de rayon r et un cercle circonscrit C de rayon R. Cette situation est illustrée sur la figure de gauche, le compact convexe est le carré violet, le cercle C est illustré en bleu et le cercle inscrit en vert. La technique utilisée consiste à considérer la zone bleue Z correspondant aux points de C qui ne sont pas dans S. La surface Z + r.B est doublement mesurée, les symboles r.B désignent ici la boule unité de rayon r et de centre le vecteur nul. Cette figure recouvre intégralement S et définit un disque de rayon R + r, illustré en jaune. On en déduit une première égalité :

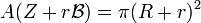
A(Z + r\mathcal B) = \pi(R+r)^2\;
Inégalité de Bonnesen (3).jpg

On découpe alors la surface Z en deux par une droite Δ passant par les centres des deux cercles inscrit et circonscrit. La partie supérieure de Z est notée Zs, comme indiquée sur l'illustration à droite. La somme de Minkowski de Zs et de r.B correspond, dans la partie supérieure à la droite Δ, à un demi-disque, de rayon R + r. Si l1 et l2 sont les longueurs des deux intersections de Z avec Δ (voir la figure), l'intersection de la somme avec la partie inférieure à la droite Δ possède une aire égale à π.r2 + (l1 + l2)r. On en déduit l'égalité :

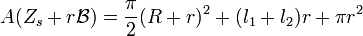
A(Z_s + r\mathcal B) = \frac{\pi}2 (R+r)^2 + (l_1 + l_2)r + \pi r^2

Il est aussi possible d'évaluer cet aire à l'aide de la formule de Steiner-Minkowski. Comme Zs n'est pas convexe, la formule est une majoration et non pas une égalité :

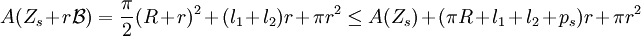
A(Z_s + r\mathcal B) = \frac{\pi}2 (R+r)^2 + (l_1 + l_2)r + \pi r^2 \le A(Z_s) + (\pi R + l_1 + l_2 + p_s)r + \pi r^2 \;

Ici ps désigne la longueur de la partie supérieure de la frontière de S. On peut appliquer exactement le même raisonnement à la partie inférieure à la droite Δ. En utilisant l'indice i pour décrire la partie inférieure, on obtient :

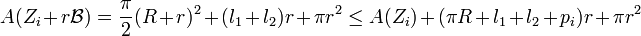
A(Z_i + r\mathcal B) = \frac{\pi}2 (R+r)^2 + (l_1 + l_2)r + \pi r^2 \le A(Z_i) + (\pi R + l_1 + l_2 + p_i)r + \pi r^2 \;

En sommant les deux majorations :

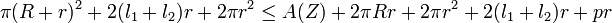
\pi (R+r)^2 + 2(l_1 + l_2)r + 2\pi r^2 \le A(Z) + 2\pi Rr + 2\pi r^2 + 2(l_1 + l_2)r + pr\;

Le périmètre p de S est en effet la somme de ps et de pi. L'aire de Z est aussi égale à la différence de l'aire d'un disque de rayon R avec l'aire a de S, ce qui donne :

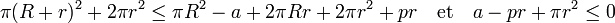
\pi (R+r)^2 + 2\pi r^2 \le \pi R^2 - a + 2\pi Rr + 2\pi r^2 + pr\quad \text{et}\quad a -pr + \pi r^2 \le 0

La dernière majoration signifie que -r est d'image négative par le polynôme associant à t l'aire de S + tB.

  • La valeur -R est d'image négative par le polynôme qui, à t associe l'aire de la surface S + t.B :

On applique exactement le même raisonnement que le précédent en remplaçant Z par C, le cercle de rayon R et le coefficient r par R, le rayon d'un cercle circonscrit. On obtient la majoration :

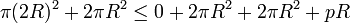
\pi (2R)^2 + 2\pi R^2 \le 0 + 2\pi R^2 + 2\pi R^2 + pR\;

La valeur 0 correspond à l'aire du cercle C. Elle est majorée par la différence entre l'aire du disque de rayon R et celle de S, on obtient :

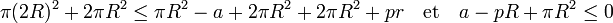
\pi (2R)^2 + 2\pi R^2 \le \pi R^2 - a + 2\pi R^2 + 2\pi R^2 + pr\quad \text{et}\quad a -pR + \pi R^2 \le 0

Ce qui démontre la proposition.

  • L'inégalité de Bonnesen est vérifiée :

Dire que -r et -R ont une image négative par le polynôme revient à dire que ces valeurs se trouvent entre les racines :

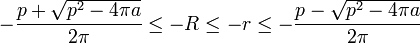
-\frac {p + \sqrt{p^2 - 4\pi a}}{2\pi} \le -R \le -r \le -\frac {p - \sqrt{p^2 - 4\pi a}}{2\pi}

Cela signifie aussi que la distance qui sépare R et r est plus petite que le rapport entre le discriminant et π :

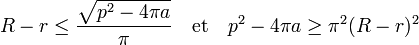
R-r \le \frac {\sqrt{p^2 - 4\pi a}}{\pi} \quad\text{et}\quad p^2 - 4\pi a \ge \pi^2(R - r)^2
  • Remarque historique :

La démonstration de la majoration est l'œuvre de Bonnesen[17] en 1921. La démonstration présentée ici, qui montre que les deux rayons sont situés entre les deux racines est celle d'Hadwiger[18] et est plus tardive.

 

Dimension supérieure

Enoncé

Une bulle de savon est une réponse naturelle au théorème isopérimétrique en dimension 3. La tension superficielle de la bulle possède une énergie potentielle minimale si sa surface l'est. L'équilibre statique est obtenu quand la surface est minimale pour enserrer la quantité d'air enfermée dans la membrane de savon. La sphère est l'unique surface réalisant cet optimum, d'où la forme de la bulle. En dimension trois, on dispose du théorème suivant :

  • Soit K un compact d'un plan euclidien de dimension 3 et dont la surface est mesurable. La boule de même surface que celle de la frontière de K possède un volume plus grand que celui de K. Si v est le volume de K et s sa surface, la majoration suivante, dite inégalité isopérimétrique est vérifiée :
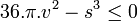
36.\pi.v^2 - s^3\le 0

De manière plus générale, si μ désigne la mesure de lebesgue dans un espace euclidien de dimension n, μn-1 la mesure équivalente pour les sous-variétés de dimension n - 1 et si K est un compact mesurable de frontière aussi mesurable, alors :

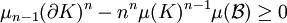
\mu_{n-1} (\partial K)^n - n^n \mu (K)^{n-1} \mu(\mathcal B) \ge 0 \;

Ici, B désigne la boule unité. Un rapide calcul permet de déduire de cette majoration les inégalités isopérimétriques pour n égal à 2 ou 3.

Difficultés

Un lampion peut posséder une surface plus grande que celle du cylindre qui le circonscrit.

Certaines démonstrations, établies en dimension 2, se généralisent aisément aux dimensions quelconques. C'est, par exemple, le cas pour la formule de Leibnitz donnant l'expression d'un déterminant. Un résultat faisant appel à la topologie est très souvent beaucoup plus complexe à établir. Un exemple célèbre est celui de la conjecture de Poincaré. Si le résultat équivalent en dimension 2 est relativement simple, en dimension 3 il s'avère redoutable à démontrer. Sans atteindre des extrêmes aussi techniques, démontrer le théorème isopérimétrique pour un espace euclidien de dimension quelconque est plus ardu qu'en dimension 2.

Une première difficulté, déjà citée, provient du fait qu'il n'existe pas de suite infinie de polygones réguliers convexes à partir de la dimension 3. Cependant, un contournement est aisément imaginable.

La géométrie des convexes diffère. A partir de la dimension 3, une enveloppe convexe d'un compact n'est pas nécessairement de frontière de mesure plus petite que la mesure de la frontière du compact. Un contre exemple est donné en dimension 3 par une variété analogue à la chambre à air d'un vélo. Son enveloppe convexe contient deux disques supplémentaires, dont l'aire peut être supérieure à celle de la moitié de la surface de la variété qui n'est pas à la frontière de l'enveloppe convexe.

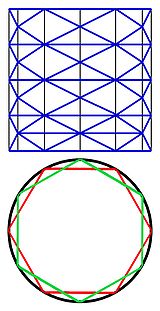
Enfin, le sens à donner au mot mesure de la frontière n'est pas aussi simple à partir de la dimension 3, que dans le plan. Dans le plan, définir la longueur d'une courbe est aisé avec l'approche de Jordan, on considère la borne supérieure de l'ensemble des lignes polygonales sont les sommets sont ordonnés et situés sur la courbe (cf l'article Longueur d'un arc). A partir de la dimension 3, cette démarche n'est plus possible, il existe des suites de polyèdres dont les points sont tous sur la surface d'une portion de cylindre située entre deux plans parallèles dont la suite des surfaces diverge. Un exemple est donné sur la figure de droite. La notion de forme volume permet bien de définir une mesure n - 1 dimensionnelle pour la frontière du compact, elle suppose cependant que la frontière est suffisamment lisse, c'est-à-dire qu'elle définisse une variété de dimension n - 1 de classe C2.

Variété différentielle

Contenu de Minkowski

Le contenu 1 dimensionnel d'un lacet simple correspond à longueur de l'arc, au sens de Jordan.

Pour obtenir une définition générale de la mesure de la frontière du compact étudié dans un espace euclidien E de dimension n, Minkowski définit la notion de contenu k dimensionnel, ici k désigne un entier plus petit que n. Soit D un compact fermé de E, son contenu k dimensionnel Mn-k(D) est le suivant[19] :

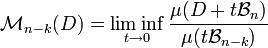
\mathcal M_{n-k} (D) = \liminf_{t \to 0} \frac {\mu (D + t\mathcal B_n)}{\mu(t\mathcal B_{n-k})}

Ici, Bp désigne la boule unité d'un espace euclidien de dimension p. En toute rigueur, on devrait parler de contenu k dimensionnel inférieur. La figure de droite illustre le concept pour la frontière d'un compact. La partie supérieure de la fraction définissant le contenu correspond au volume d'un tube de section un disque de rayon t si la figure est en dimension 3. Si la frontière est une variété de classe C2, le volume du tube est égal à sa longueur que multiple la surface du disque de rayon t, si t n'est pas trop grand. Le rapport définissant le contenu est toujours égal à la longueur de la variété[20]

Dans le cas plus général d'une variété compacte de dimension k et de classe C2, le volume du tube s'exprime comme un polynôme de degré n - k dont le terme de plus petit degré est égal à la mesure de la variété. La mesure est alors définie à l'aide de la forme volume canonique. Ce résultat ce conçoit bien intuitivement, l'intersection du tube en un point de la variété par l'espace affine orthogonal à la variété en ce point est une boule de dimension n - k et de rayon t. En première approximation, le volume du tube est le produit de la mesure de cette boule par celle de la variété.

Egalité isopérimétrique pour la boule

Le choix du contenu de Minkowski pour mesurer la frontière du compact considéré est pertinent. On peut s'en rendre compte par l'étude de l'égalité isopérimétrique dans le cas d'une boule r.B de rayon r d'un espace euclidien E de dimension n. Sa mesure est égale à[21] :

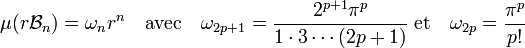
\mu(r\mathcal B_n) = \omega_n r^n \quad\text{avec}\quad \omega_{2p+1} = \frac {2^{p+1}\pi^p}{1\cdot 3 \cdots (2p+1)}\;\text{et}\quad \omega_{2p} = \frac {\pi^{p}}{p!}

Si la surface est désignée par la lettre S, on a :

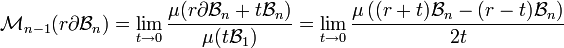
\mathcal M_{n-1}(r\partial {\mathcal B_n}) = \lim_{t \to 0} \frac {\mu (r\partial {\mathcal B_n} + t\mathcal B_n)}{\mu(t\mathcal B_{1})} = \lim_{t \to 0} \frac {\mu \left((r+t) {\mathcal B_n} - (r-t) {\mathcal B_n}\right)}{2t}

La deuxième égalité indique que le tube engendré par la surface Sn-1 est composé des points de la boule de rayon r + t qui ne sont pas éléments de la boule r - t. Ce volume se calcule aisément :

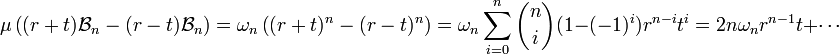
\mu \left((r+t) {\mathcal B_n} - (r-t) {\mathcal B_n}\right) = \omega_n\left((r+t)^n - (r-t)^n\right) = \omega_n \sum_{i=0}^n \binom ni (1 - (-1)^i)r^{n-i}t^i = 2n\omega_n r^{n-1}t + \cdots

On en déduit :

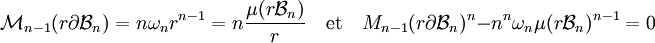
\mathcal M_{n-1}(r\partial {\mathcal B_n}) = n\omega_n r^{n-1} = n \frac {\mu (r\mathcal B_n)}r\quad\text{et}\quad M_{n-1}(r\partial {\mathcal B_n})^n - n^n\omega_n \mu(r\mathcal B_n)^{n-1} = 0

Ce qui est bien l'égalité isopérimétrique.

Inégalité de Brunn-Minkowski

L'inégalité de Brunn-Minkowski permet aisément de démontrer l'inégalité isopérimétrique, dans le cas d'un compact non vide K. Appliquée à K et à t.B, on obtient :

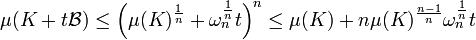
\mu(K + t\mathcal B) \le \left(\mu(K)^{\frac 1n} + \omega_n^{\frac 1n} t\right)^n \le \mu(K) + n\mu(K)^{\frac {n-1}n} \omega_n^{\frac 1n} t

Autrement dit :

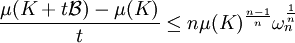
\frac {\mu(K + t\mathcal B) - \mu(K)}t \le n\mu(K)^{\frac {n-1}n} \omega_n^{\frac 1n}

Il suffit de remarquer que le terme de gauche admet pour limite inférieure le contenu n - 1 dimensionnel de la frontière de K. Ce résultat est connu sous le nom de formule de Steiner-Minkowski. On obtient :

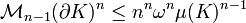
\mathcal M_{n-1}(\partial K)^n \le n^n\omega^n \mu(K)^{n-1}

Ce qui correspond bien à l'inégalité isopérimétrique. Aucune hypothèse n'a été faite sur la nature du compact K.[22]

Inégalité d'Alexandrov-Fenchel

La démonstration est à la fois simple et rapide, mais il manque l'unicité de la solution. Des hypothèses supplémentaires permettent une démonstration plus simple de cette unicité. Le cas général ne peut s'exprimer aisément ; pour s'en rendre compte, il suffit de considérer une boule dans laquelle on plante une aiguille infiniment fine. Il existe deux cas où le théorème isopérimétrique s'exprime aisément. Dans le cas des convexes compacts, ou dans le cas des variétés à bord de classe C2, l'unicité de l'optimum se démontre à l'aide de l'inégalité d'Alexandrov-Fenchel.

Voir aussi

Notes

  1. ↑ T. Heath A History of Greek Mathematics, Vol. 2 Dover Publications (1981) (ISBN 0486240746)
  2. ↑ P. Nahin When Least Is Best: How Mathematicians Discovered Many Clever Ways to Make Things as Small (or as Large) as Possible Princeton University Press p 47 (2007) (ISBN 0691130523)
  3. ↑ P. J. Nahin When Least Is Best: How Mathematicians Discovered Many Clever Ways to Make Things as Small (or as Large) as Possible Princeton University Press (2003) p 55-56 (ISBN 0691070784)
  4. ↑ Cette remarque est issue de : R. Osserman The isoperimetric inequality Bull. Amer. Math. Soc. Vol 84 (1978) p 1188
  5. ↑ F. Dress Quelques grands problèmes en mathématiques Bulletin de la société mathématiques de France T 115 (1987) p 43
  6. ↑ H. Liebmann Ueber die Verbiegung der geschlossenen Flächen positiver Krümmung Math. Ann. 53 (1900) p 81-112
  7. ↑ H. A. Schwarz Gesammelte Mathematische Abhandlung Springer-Verlag Berlin (1890) I Vol. 2 p 327
  8. ↑ L'essentiel des informations de ce paragraphe provient de : R. Osserman The isoperimetric inequality Bull. Amer. Math. Soc. Vol 84 (1978)
  9. ↑ H. MinkowskiGesammelte Abhandlungen Chelsea Pub Co 1967 (réédition de l'original de 1911) Vol 2 p 131-229 (ISBN 0828402086)
  10. ↑ Bonnesen T Sur une amélioration de l'inégalité isopérimetrique du cercle et la démonstration d'une inégalité de Minkowski C. R. Acad. Sci. Paris 172 (1921) p 1087–1089
  11. ↑ W. Fenchel Inégalités quadratiques entre les volumesmixtes des corps convexes Comptes Rend. Acad. Sci. Paris 203 (1936), p. 647-650 et A. D. Alexandrov Neue Ungleichungen für die Mischvolumen konvexer Körper Dokl. Acad. Sci. URSS 14 (1937), p. 155-157
  12. ↑ Les deux derniers paragraphes proviennent essentiellement de : B. Teissier Volumes des corps convexes, géométrie et algèbre Institut de Mathématiques de Jussieu. Leçon donnée le jeudi 7 octobre 1999 Rédigée par C. Reydy
  13. ↑ A P Burton P Smith Isoperimetric inequalities and areas of projections in Rn Acta Mathematica Hungarica Vol 62, N° 3-4 (1993)
  14. ↑ On trouve une démonstration, par exemple à : A. Treibergs Inequalities that Imply the Isoperimetric Inequality University of Utah
  15. ↑ A. Treibergs Inequalities that Imply the Isoperimetric Inequality University of Utah
  16. ↑ B. Teissier Volumes des corps convexes, géométrie et algèbre Institut de Mathématiques de Jussieu. Leçon donnée le jeudi 7 octobre 1999 Rédigée par C. Reydy p 5
  17. ↑ T. Bonnesen Über eine Verschärfung der isoperimetrischen Ungleichheit des Kreises in der ebene und auf der Kugeloberfläche nebst einer Anwendung auf eineMinkowskischeUngleichheit für konvexe Körper Math. Annalen 84 (1921) p. 216-227
  18. ↑ H. Hadwiger Vorlesungen Über Inhalt, Oberfläche und Isoperimetrie Springer, Berlin (1957) p. 153
  19. ↑ On trouve cette définition dans : R. Osserman The isoperimetric inequality Bull. Amer. Math. Soc. Vol 84 (1978) p 1189
  20. ↑ Marcel Berger, Bernard Gostiaux, Géométrie différentielle : variétés, courbes et surfaces [détail des éditions] p 254
  21. ↑ Marcel Berger, Bernard Gostiaux, Géométrie différentielle : variétés, courbes et surfaces [détail des éditions] p 227
  22. ↑ Cette démonstration provient de : R. Osserman The isoperimetric inequality Bull. Amer. Math. Soc. Vol 84 (1978) p 1190

Références

  • Marcel Berger, Bernard Gostiaux, Géométrie différentielle : variétés, courbes et surfaces [détail des éditions]
  • Y.D Burago, V.A. Zallgaller, Geometric inequalities, Springer Grundlehren Math. 285, Springer 1988
  • Portail de la géométrie Portail de la géométrie
Ce document provient de « Th%C3%A9or%C3%A8me isop%C3%A9rim%C3%A9trique ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme isoperimetrique de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Théorème isopérimétrique — En géométrie, un théorème isopérimétrique traite d une question concernant les compacts d un espace métrique muni d une mesure. Un exemple simple est donné par les compacts d un plan euclidien. Les compacts concernés sont ceux de mesures finies… …   Wikipédia en Français

  • Theoreme d'inversion locale — Théorème d inversion locale En mathématiques, le théorème d inversion locale est un résultat de géométrie différentielle. Il indique que si une fonction f est continûment différentiable en un point a, si cette différentielle est une bijection… …   Wikipédia en Français

  • Théorème de Bessel-Parseval-Plancherel — Égalité de Parseval Pour les articles homonymes, voir Parseval. L égalité de Parseval (parfois appelée également Théorème de Parseval ou Identité de Rayleigh) est une formule fondamentale de la théorie des séries de Fourier. On la doit au… …   Wikipédia en Français

  • Théorème de Parseval — Égalité de Parseval Pour les articles homonymes, voir Parseval. L égalité de Parseval (parfois appelée également Théorème de Parseval ou Identité de Rayleigh) est une formule fondamentale de la théorie des séries de Fourier. On la doit au… …   Wikipédia en Français

  • Inegalite isoperimetrique — Inégalité isopérimétrique Cet article court présente un sujet plus amplement développé ici : Isopérimétrie. En géométrie, aussi bien en géométrie euclidienne qu en géométrie riemannienne, on appelle inégalité isopérimétrique toute inégalité… …   Wikipédia en Français

  • Inégalité Isopérimétrique — Cet article court présente un sujet plus amplement développé ici : Isopérimétrie. En géométrie, aussi bien en géométrie euclidienne qu en géométrie riemannienne, on appelle inégalité isopérimétrique toute inégalité portant sur le volume… …   Wikipédia en Français

  • Inégalité isopérimétrique — Cet article court présente un sujet plus développé dans : Isopérimétrie. En géométrie, aussi bien en géométrie euclidienne qu en géométrie riemannienne, on appelle inégalité isopérimétrique toute inégalité portant sur le volume (longueur,… …   Wikipédia en Français

  • Isoperimetrie — Isopérimétrie La forme d une bulle de savon est une réponse à une question d isopérimétrie. Sa géométrie est sphérique car c est le solide qui englobe le plus vaste volume dans une surface de mesure donnée. En géométrie plane, l isopérimétrie… …   Wikipédia en Français

  • Isopérimetrie — Isopérimétrie La forme d une bulle de savon est une réponse à une question d isopérimétrie. Sa géométrie est sphérique car c est le solide qui englobe le plus vaste volume dans une surface de mesure donnée. En géométrie plane, l isopérimétrie… …   Wikipédia en Français

  • Isopérimétrie — La forme d une bulle de savon est une réponse à une question d isopérimétrie : elle forme une sphère car c est le solide qui minimise la surface pour englober un volume donné, ce qui correspond au même problème de forme que de maximiser le… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”