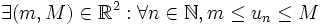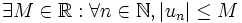Suite bornee

Suite bornee

Suite bornée

Une suite réelle 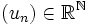(u_n) \in \mathbb{R}^\mathbb{N} est dite bornée si :

\exists (m,M) \in \mathbb{R}^2 : \forall n \in \mathbb{N}, m \leq u_n \leq M\,

ou de façon équivalent si :

\exists M \in \mathbb{R} : \forall n \in \mathbb{N}, | u_n | \leq M\,

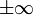Autrement dit, l'ensemble des ses termes est compris entre une borne supérieure et une borne inférieure. On peut déduire de façon immédiate qu'une suite bornée ne diverge pas vers \pm \infty.

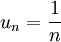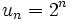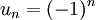Par exemple, u_n = \frac 1n est bornée puisqu'elle est décroissante et minorée (majorée par 1 et minorée par 0), alors que u_n = 2^n\, ne l'est pas car elle tend vers + \infty. Cependant une suite peut ne pas converger tout en étant bornée : u_n = (-1)^n\, est bornée (majorée par 1 et minorée par -1) mais n'admet pas de limite.

Valeurs d'adhérence pour une suite réelle bornée

Un des grands intérêts des suites bornées réside dans le fait que de toute suite bornée, on peut extraire une sous-suite convergente. En voici une démonstration imagée. Cette propriété des suites réelles porte parfois le nom de propriété de Bolzano-Weierstrass (et la démonstration se trouve dans l'article); elle est étroitement liée à la propriété de Borel-Lebesgue.

Soit (xn) une suite réelle bornée. Voyons les entiers n comme des individus situés à une hauteur xn, alignés les uns derrière les autres sur une plage, avec la mer à l'infini.

On dit que n a « vue sur la mer » si, quel que soit p > n, xn > xp. (l'individu n est plus haut que tous ceux qui viennent après lui).

On dit que n a « la vue bouchée » s'il existe p > n, xp ≥ xn. (Il existe un individu d'indice p supérieur à n et situé plus haut que lui).

Il y a alors deux cas :

  1. Ou bien il y a une infinité d'individus ayant vue sur la mer. Dans ce cas, les xn correspondant forment une sous-suite décroissante. Étant minorée, elle converge.
  2. Ou bien il n'y a qu'un nombre fini d'individus ayant vue sur la mer. Se plaçant au-delà de ce nombre fini, tous les autres individus ont la vue bouchée. On en choisit un d'indice p0. Il existe un indice p1 > p0 tel que 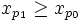x_{p_1} \ge x_{p_0} puis p2 > p1 tel que 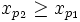x_{p_2} \ge x_{p_1}, etc. On définit ainsi une sous-suite croissante. Étant majorée, elle converge.

Remarque : La démonstration ne donne pas de construction explicite de la sous-suite. En effet, pour une suite quelconque, on est en général incapable de décider laquelle des deux affirmations 1) ou 2) est vérifiée. L'existence de la sous-suite est donc purement formelle. Il existe évidemment des cas particuliers où l'on peut construire explicitement une telle sous-suite.

Exemples

  • Si xn = (–1)n, alors la sous-suite des termes de rang pair (x2n) converge vers 1 et la sous-suite des termes de rang impairs (x2n+1) converge vers –1.
  • On peut ne pas être capable d'expliciter une telle sous-suite. Par exemple, il existe des entiers n1, n2, ..., nk, ... strictement croissants tels que sin(nk) converge, mais on n'en possède pas d'expression.
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Suite born%C3%A9e ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Suite bornee de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Suite bornée — Une suite réelle est dite bornée si : ou de façon équivalent si : Autrement dit, l ensemble de ses termes est compris entre une borne supérieure et une borne inférieure. On peut déduire de façon immédiate qu une suite bornée ne diverge… …   Wikipédia en Français

  • Suite (mathematiques elementaires) — Suite (mathématiques élémentaires) Cet article fait partie de la série Mathématiques élémentaires Algèbre Logique Arithmétique Probabilités …   Wikipédia en Français

  • Suite (mathématiques élémentaires) — Intuitivement une suite réelle est une règle qui associe à chaque entier naturel n un certain nombre réel ; on dit alors que ce nombre réel est indexé par l’entier. En fait une suite est un moyen d’indexer des nombres réels par des entiers… …   Wikipédia en Français

  • Suite convergente — Limite de suite De manière intuitive, la limite d une suite est l élément dont les termes de la suite se rapprochent quand les indices deviennent très grands. Cette définition intuitive n est guère exploitable car il faudrait pouvoir définir le… …   Wikipédia en Français

  • Suite divergente — Limite de suite De manière intuitive, la limite d une suite est l élément dont les termes de la suite se rapprochent quand les indices deviennent très grands. Cette définition intuitive n est guère exploitable car il faudrait pouvoir définir le… …   Wikipédia en Français

  • Suite extraite — Sous suite En mathématiques, une sous suite (ou une suite extraite) est une suite obtenue en ne prenant que certains éléments (une infinité) d une suite de départ. Cette opération est parfois appelée extraction. Formellement, une suite est une… …   Wikipédia en Français

  • Suite de cauchy — Pour les articles homonymes, voir Cauchy. Augustin Louis Cauchy En analyse mathématique, une suite de Cauchy est une …   Wikipédia en Français

  • Suite (mathématiques) — Pour les articles homonymes, voir Suite. En mathématiques, une suite[1] est une famille d éléments indexée par les entiers naturels. Une suite finie est une famille indexée par les entiers strictement positifs inférieurs ou égaux à un certain… …   Wikipédia en Français

  • Suite de Cauchy — Pour les articles homonymes, voir Cauchy. Augustin Louis Cauchy En analyse mathématique, une suite de Cauchy est une suite de réels, de complexes, de points d …   Wikipédia en Français

  • Suite aliquote — En arithmétique, une suite aliquote est une suite d entiers dans laquelle chaque nombre est la somme des diviseurs propres[1] de son prédécesseur. Quand la suite atteint 1, elle s arrête car 1 ne possède pas de diviseur propre. Ainsi la suite… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”