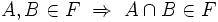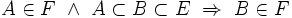Filtre (Mathématiques)

La théorie des filtres a été inventée, en 1937, par Henri Cartan^[1],[2] et utilisée par Nicolas Bourbaki dans le Livre III : Topologie générale de ses Éléments de mathématique.

Sommaire 1 Definition générale 2 Finesse d'un filtre 3 Cas particuliers 3.1 Filtre sur un ensemble 3.1.1 Propriété 3.1.2 Exemples 3.1.3 Base de filtre 4 Filtres en Topologie 5 Notes 6 Bibliographie 7 Voir aussi 8 Liens externes

Definition générale

En mathématiques, un filtre est une partie F non vide d'un ensemble partiellement ordonné (P,≤) vérifiant les deux conditions suivantes:

1. Pour tout x, y dans F, il existe z dans F, tel que z ≤ x et z ≤ y. (C'est une base de filtre.)
2. Pour tout x dans F et y dans P, x ≤ y implique que y est dans F.

Le filtre F est propre si et seulement si il n'est pas égal à P en entier.

Finesse d'un filtre

Soient deux filtres F et F' sur un même ensemble, F' est plus fin que F s'il possède autant ou plus d'éléments que F c'est-à-dire :

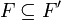
Si en plus 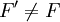, et donc que F' possède plus d'éléments que F, on dit que F' est strictement plus fin que F.

Un filtre tel qu'il n'en existe pas de strictement plus fin est un ultrafiltre.

Cas particuliers

Filtre sur un ensemble

Un cas important est celui où P=P(E) est l'ensemble des parties d'un ensemble E, ordonné par l'inclusion:

Propriété

F est un filtre sur E (ie: dont les valeurs sont dans P(E)) ssi

1. 
2. 

Ce sont respectivement les parties 1 et 2 de la définition d'un filtre.

Cela implique: 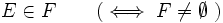Puisqu'un filtre est un ensemble non vide, il possède un élement A de P(E), et puisque 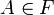et 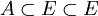alors d'après la propriété 2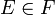

F est un filtre propre sur E ssi en plus 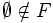. Sinon d'après la propriété 2, F=P(E) tout entier, ce qui est sans intérêt. Avoir un filtre propre permet également d'éviter d'avoir 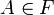et 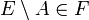simultanément.

Exemples

L'ensemble de toutes les parties de E contenant une partie non vide donnée A de E (en particulier, un singleton A={x}), forme un filtre sur E, appelé filtre principal engendré par A.

Le filtre de Fréchet sur un ensemble infini E est l'ensemble des parties de E ayant un complément fini dans E.

Un ultrafiltre sur un ensemble E est un filtre tel qu'il n'existe aucun filtre sur E strictement plus fin que lui. Cela signifie qu'un ultrafiltre est un élément maximal de l'ensemble des filtres ordonnés par l'inclusion.

Soit E un espace topologique non vide et x un élément de E. L'ensemble des voisinages de x est un filtre sur E.

Base de filtre

Si B est une partie de P(E) ne contenant pas l'ensemble vide et telle que l'intersection de deux éléments de B contient un élément de B, alors il existe un unique filtre minimal F contenant B, appelé filtre engendré par B, on dit alors que B est une base de filtre pour F.

Le filtre de Frechet sur a pour base 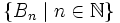où .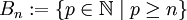

Filtres en Topologie

La théorie des filtres permet de définir une notion de convergence dans un espace topologique séparé non métrisable, où la convergence des suites ne permet pas de définir la compacité.

Soit E un espace topologique, x un élément de E . On dit qu'un filtre F sur E converge vers x ssi le filtre F est plus fin que le filtre des voisinages de x, autrement dit tout voisinage de x appartient au filtre F.

Un espace topologique séparé est compact ssi pour tout filtre F sur E, il existe un filtre plus fin que F qui converge ou encore tout ultrafiltre sur E converge.

En utilisant les ultrafiltres on peut donner une démonstration élégante ^[3] du Théorème de Tychonov.

Une fonction (en particulier une suite) f à valeurs dans un espace topologique E admet L comme limite suivant la base de filtre B, ssi pour tout voisinage V de L, il existe A dans B, tel que la restriction de f à A soit à valeurs (c-à-d. f(A) soit inclus) dans V.

Notes

Bibliographie

• Laurent Schwartz, Analyse, Topologie Générale et analyse fonctionelle, Hermann, Paris, 1970.

Voir aussi

• Topologie

Liens externes

• Henri Cartan et la notion de filtre
• Henri Cartan, Notes sur l'introduction éventuelle des "filtres" dans l'enseignement du second degré

• Portail des mathématiques