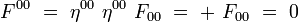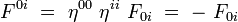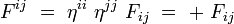- Équation de Maxwell-Gauss
-
Équations de Maxwell
Les équations de Maxwell, aussi appelées équations de Maxwell-Lorentz, sont des lois fondamentales de la physique. Elles constituent les postulats de base de l'électromagnétisme, avec l'expression de la force électromagnétique de Lorentz.
Ces équations traduisent sous forme locale différents théorèmes (Gauss, Ampère, Faraday) qui régissaient l'électromagnétisme avant que Maxwell ne les réunisse sous forme d'équations intégrales. Elles donnent ainsi un cadre mathématique précis au concept fondamental de champ introduit en physique par Faraday dans les années 1830.
Ces équations montrent notamment qu'en régime stationnaire, les champs électrique et magnétique sont indépendants l'un de l'autre, alors qu'ils ne le sont pas en régime variable. Dans le cas le plus général, il faut donc parler du champ électromagnétique, la dichotomie électrique/magnétique étant une vue de l'esprit. Cet aspect trouve sa formulation définitive dans le formalisme covariant présenté dans la seconde partie de cet article : le champ électromagnétique y est représenté par un être mathématique unique : le tenseur électromagnétique, dont certaines composantes s'identifient à celles du champ électrique et d'autres à celles du champ magnétique.
Cet article fait partie de la série
formulaire de physiqueOptique Électro- Magnéstatique Physique quantique Thermodynamique Mécanique des fluides Mécanique Relativité restreinte Trou noir Analyse vectorielle Aspects historiques
L'apport de Maxwell
Vers 1865, Maxwell a réalisé une synthèse harmonieuse des diverses lois expérimentales découvertes par ses prédécesseurs (lois de l'électrostatique, du magnétisme, de l'induction...), en les exprimant sous la forme d'un système de quatre équations aux dérivées partielles couplées. Elles furent publiées dans leur forme définitive en 1873 dans l'ouvrage Electricity and Magnetism.
Mais cette synthèse n'a été possible que parce que Maxwell a su dépasser les travaux de ses devanciers, en introduisant dans une équation un « chaînon manquant », appelé le courant de déplacement, dont la présence assure la cohérence de l'édifice unifié.
Les héritiers de Maxwell
La synthèse de Maxwell a permis ultérieurement les deux plus grandes avancées de la physique moderne :
- la théorie de la relativité restreinte (via le problème du référentiel de l'hypothétique éther ). En effet, les équations de Maxwell permettent de prédire l'existence d'une onde électromagnétique, c'est-à-dire que la modification d'un des paramètres (densité de charge, intensité du courant...) a des répercussions à distance avec un certain retard. Or, la vitesse de ces ondes, c, calculée avec les équations de Maxwell, est égale à la vitesse de la lumière mesurée expérimentalement. Cela a permis de conclure que la lumière était une onde électromagnétique. Le fait que c soit la même dans toutes les directions et indépendante du référentiel, conclusion que l'on tire de ces équations, est un des fondements de la théorie de la relativité restreinte. Si l'on change de référentiel, le changement de coordonnées classique ne s'applique pas aux équations de Maxwell, il faut utiliser une autre transformation : la transformation de Lorentz. Einstein a tenté d'appliquer les transformations de Lorentz à la mécanique classique, ce qui l'a conduit à la théorie de la relativité restreinte.
- la physique quantique. L'étude de la lumière et des ondes électromagnétiques, avec notamment les travaux de Max Planck sur le corps noir et d'Heinrich Hertz sur l'effet photo-électrique, donna naissance à la théorie quantique en 1900.
Théorie de Maxwell-Lorentz dans le vide
On présente ci-dessous la théorie microscopique fondamentale qui donne les équations de Maxwell-Lorentz dans le vide en présence de sources, qui peuvent être des charges ponctuelles et/ou leurs courants électriques microscopiques associés si ces charges sont en mouvement dans le référentiel d'étude.
La théorie macroscopique nécessitant l'introduction des champs D et H (et les équations de Maxwell associées) est discutée en détail dans Électrodynamique des milieux continus.
On note :
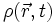 la densité volumique de charge électrique au point
la densité volumique de charge électrique au point 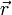 à l'instant t.
à l'instant t. le vecteur densité de courant.
le vecteur densité de courant.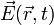 le vecteur champ électrique.
le vecteur champ électrique.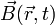 le pseudo-vecteur induction magnétique.
le pseudo-vecteur induction magnétique.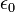 la permittivité diélectrique du vide.
la permittivité diélectrique du vide.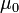 la perméabilité magnétique du vide.
la perméabilité magnétique du vide.
Équation de Maxwell-Gauss
L'équation locale de Maxwell
Cette équation locale donne la divergence du champ électrique en fonction de la densité de la charge électrique :
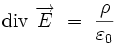
Cette équation correspond à un « terme de source » : la densité de charge électrique est une source du champ électrique. Par exemple, pour une charge ponctuelle
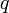 fixée à l'origine
fixée à l'origine 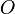 , la loi de Coulomb donnant le champ électrostatique en un point
, la loi de Coulomb donnant le champ électrostatique en un point 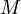 de l'espace, point repéré par le vecteur position
de l'espace, point repéré par le vecteur position 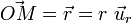 où
où 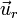 est le vecteur unitaire radial, s'écrit :
est le vecteur unitaire radial, s'écrit :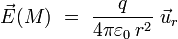
Ce champ électrostatique vérifie l'équation de Maxwell-Gauss pour la source statique :
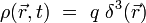
où
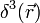 est la distribution de Dirac dans l'espace à trois dimensions.
est la distribution de Dirac dans l'espace à trois dimensions.Le théorème de Gauss
L'équation de Maxwell-Gauss est héritée du théorème de Gauss, qui permet de lier le flux du champ électrique à travers une surface fermée à la charge intérieure à cette surface :
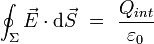
où
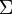 est une surface fermée arbitraire, appelée surface de Gauss, et
est une surface fermée arbitraire, appelée surface de Gauss, et 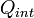 la charge électrique totale intérieure à cette surface
la charge électrique totale intérieure à cette surface 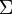 [1].
[1].On remarquera que l'équation de Maxwell-Gauss se retrouve facilement en appliquant le théorème d'Ostrogradski au théorème de Gauss et en prenant un volume infinitésimal.
Équation de Maxwell de conservation du flux (Équation de Maxwell-Thomson)
Le flux du champ magnétique à travers une surface
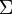 fermée est toujours identiquement nul :
fermée est toujours identiquement nul :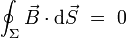
L'équation locale de Maxwell
Cette équation locale est au champ magnétique ce que l'équation de Maxwell-Gauss est au champ électrique, à savoir une équation avec « terme de source », ici identiquement nul :
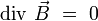
Elle traduit le fait expérimental suivant : il n'existe pas de monopôle magnétique. Un monopôle magnétique serait une source ponctuelle de champ magnétique, analogue de la charge électrique ponctuelle pour le champ électrique. Or, l'objet de base source d'un champ magnétique est l'aimant, qui se comporte comme un dipôle magnétique : un aimant possède en effet un pôle nord et un pôle sud. L'expérience fondamentale consistant à tenter de couper un aimant en deux donne naissance à deux aimants, et non un pôle nord et un pôle sud séparément[2].
Introduction du potentiel-vecteur
L'analyse vectorielle montre que la divergence d'un rotationnel est toujours identiquement nulle :
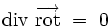
Réciproquement, toute fonction dont la divergence est identiquement nulle peut être exprimée sous la forme d'un rotationnel.
L'équation locale de conservation du flux magnétique permet donc de définir au moins localement[3] un potentiel-vecteur
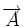 tel que :
tel que :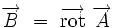
Le problème important de l'unicité du potentiel-vecteur est discuté dans l'article Invariance de jauge de la théorie.
Équation de Maxwell-Faraday
Cette équation locale traduit le phénomène fondamental d'induction électromagnétique découvert par Faraday.
L'équation locale
Elle donne le rotationnel du champ électrique en fonction de la dérivée temporelle du champ magnétique :
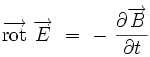
Cela correspond à un « terme variationnel » : la variation du champ magnétique crée un champ électrique. Sa forme intégrale est la loi de Faraday :
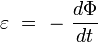
où
 , est la force électromotrice d'induction dans un circuit électrique et
, est la force électromotrice d'induction dans un circuit électrique et 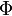 le flux magnétique à travers ce circuit.
le flux magnétique à travers ce circuit.Introduction du potentiel électrique
L'analyse vectorielle montre que le rotationnel d'un gradient est toujours identiquement nul :
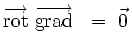
L'équation de Maxwell-Faraday couplée à l'existence locale d'un potentiel-vecteur
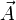 permettent de définir (au moins localement) le potentiel électrique
permettent de définir (au moins localement) le potentiel électrique 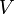 (scalaire) tel que :
(scalaire) tel que :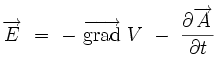
Le problème important de l'unicité du potentiel électrique est discuté dans Invariance de jauge de la théorie.
Équation de Maxwell-Ampère
L'équation locale de Maxwell
Cette équation est héritée du théorème d'Ampère. Sous forme locale, elle s'écrit en termes du vecteur densité de courant
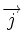 :
: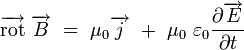
Introduction du courant de déplacement
L'équation précédente peut se réécrire :
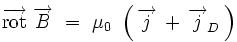
en introduisant le courant de déplacement de Maxwell :
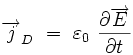
La forme intégrale lie la circulation du champ magnétique sur un contour C fermé, et les courants qui traversent la surface s'appuyant sur ce contour :
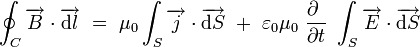
Équation de conservation de la charge
Prenons la divergence de l'équation de Maxwell-Ampère :
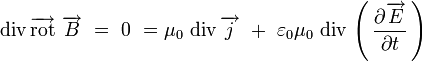
On peut écrire en permutant les dérivées spatiales et temporelles, puis en utilisant l'équation de Maxwell-Gauss :
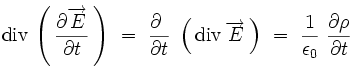
On obtient finalement l'équation locale de conservation de la charge électrique :
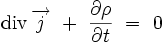
La présence du terme de courant de déplacement, introduit par Maxwell, est essentielle à l'obtention de cette équation.
Invariance de jauge de la théorie
L'analyse vectorielle montre que la divergence d'un rotationnel est toujours identiquement nulle :
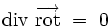
L'équation locale de conservation du flux magnétique permet donc de définir au moins localement [4] un potentiel-vecteur
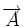 tel que :
tel que :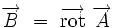
L'analyse vectorielle nous dit également que
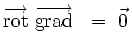
Alors le potentiel-vecteur n'est pas défini de manière unique puisque la transformation suivante, avec
 une fonction quelconque
une fonction quelconque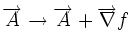
ne modifie par la valeur du champ
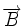 . Ceci est un exemple de transformation de jauge. Il faut donc imposer des conditions supplémentaires pour déterminer
. Ceci est un exemple de transformation de jauge. Il faut donc imposer des conditions supplémentaires pour déterminer 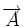 de façon non-ambigüe. On appelle cela des conditions de jauge, par exemple la jauge de Coulomb ou encore la jauge de Lorenz.
de façon non-ambigüe. On appelle cela des conditions de jauge, par exemple la jauge de Coulomb ou encore la jauge de Lorenz.Le lecteur notera qu'en physique classique, le potentiel-vecteur semble n'être qu'un outil mathématique commode pour analyser les solutions des équations de Maxwell, mais ne semble pas être une grandeur physique directement mesurable. En 1959, dans le cadre de la physique quantique, Aharonov et Bohm ont démontré[5] que le potentiel-vecteur avait un effet observable en mécanique quantique : c'est l'effet Aharonov-Bohm.
L'analyse vectorielle montre que le rotationnel d'un gradient est toujours identiquement nul :
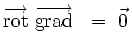
L'équation de Maxwell-Faraday couplée à l'existence locale d'un potentiel-vecteur
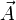 permettent de définir (au moins localement) le potentiel électrique
permettent de définir (au moins localement) le potentiel électrique 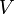 (scalaire) tel que :
(scalaire) tel que :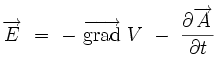
Le potentiel
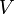 lui non plus n'est pas défini de façon unique mais la transformation de jauge associée est liée à celle de
lui non plus n'est pas défini de façon unique mais la transformation de jauge associée est liée à celle de 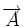 est la suivante (on rappelle celle de
est la suivante (on rappelle celle de 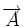 par souci de clarté) et on a
par souci de clarté) et on a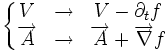
Ces deux équations donnent l'invariance de jauge complète des équations de Maxwell.
Solutions des équations du champ électromagnétique.
Pour simplifier, conformément à la pratique, nous attribuerons ces équations à Maxwell, en les appelant « équations de Maxwell » (EM).
Solutions mathématiques des équations de Maxwell dans le vide.
Résolvons les EM dans l 'espace éventuellement limité par des conditions qui gardent la linéarité.
Représentons des solutions par des lettres Q, R, ...( ensembles des 6-vecteurs formés des six composantes du champ en tout point de coordonnées x, y, z, t ). Par définition de la linéarité, αQ + βR + ..., où α, β ... sont des constantes réelles est une solution. En conséquence, les solutions sont représentées par les points d'un espace vectoriel réel. Conformément à la définition introduite en acoustique, un mode est un rayon de cet espace. Un système complet de solutions constitue un repère dans cet espace nommé tantôt espace des solutions, tantôt espace des modes. Une solution particulière dans un mode est obtenue en multipliant un champ de ce mode posé comme champ d'amplitude unité, par une constante réelle, l'amplitude.
Avec un système d'unités convenable, l'énergie W(Q) d'une solution Q est l'intégrale étendue à tout l'espace, à un instant donné, de Q ² ; on oublie très souvent que cette équation est non-linéaire, de sorte que si on peut ajouter des champs, les énergies correspondantes ne s'ajoutent pas. En considérant que W(Q) est le carré scalaire de Q, par des processus d'orthogonalisation de Schmitt, on obtient des systèmes complets de solutions orthogonales, ou encore des systèmes complets de modes orthogonaux. Dans ces systèmes, les énergies sont indépendantes.
Planck a posé que l'énergie dans un mode monochromatique de fréquence ν se propageant dans un corps noir à la température T est w = hν/(exp(hν/kT)-1)+K. La valeur erronée de K donnée par Planck a été corrigée par Nernst en 1916 ; la valeur K = hν/2 est facilement retrouvée car la thermodynamique impose que w tende vers kT lorsque T tend vers l'infini. Cette formule définit la température d'un mode. Cependant l'interprétation de cette formule est physiquement délicate car la définition d'une fréquence pure ν suppose une expérience de durée infinie.
Introduction des charges électriques
On sait calculer les champs émis par des charges, par exemple le champ émis par un dipôle électrostatique oscillant. Pour se ramener au problème précédent, on utilise le « truc de Schwarzschild et Fokker ». Le champ émis par une source est nommé « champ retardé » QR. Dépouillé de la source, ce champ n'est pas solution des EM. Pour obtenir une solution identique dans le futur, il faut lui ajouter un « champ avancé » QA. Par cette définition, QA + QR est solution des EM. Ainsi, en substituant le champ avancé à la source, on est ramené au problème linéaire d'un champ dans le vide et on peut définir des modes.
Solutions physiques des équations de Maxwell.
Le mathématicien est libre d'ignorer des contingences physiques en faisant, de façon plus ou moins implicite, des hypothèses irréalistes ; ainsi nous avons supposé qu'il existe des systèmes électromagnétiques isolés dans lesquels il est loisible d'introduire quelques champs choisis ; l'établissement de la loi de Planck est un exemple remarquable de cette hypothèse. Montrons que cette hypothèse est physiquement absurde.
Sauf peut-être dans les étoiles à neutrons, la matière est constituée de particules petites par rapport à leurs distances. Ces particules sont les sources des champs électromagnétiques ; le champ émis par une particule décroît avec la distance, il est donc beaucoup plus intense en son voisinage qu'à proximité d'autres particules. Or l'absorption d'un champ est l'addition d'un champ opposé ; la génération d'un tel champ est difficilement et approximativement obtenue pour obtenir une absorption active en acoustique, au moyen de haut parleurs, pour réduire l'intensité d'un bruit. La génération de l'opposé du champ électromagnétique créé par une particule, intense en son voisinage requiert l'addition des champs faibles créés par de nombreuses autres particules, ce qui ne fait que compliquer le problème qui apparaît ainsi insoluble : il subsiste un champ résiduel stochastique loin des sources.
L'existence nécessaire de champs résiduels, connue, semble-t-il depuis longtemps, est exploitée, dans le cadre de l'électromagnétisme, depuis la fin du dix-neuvième siècle par les charlatans qui se reconnaissent sous des noms tels que « radiesthésistes ». En électromagnétisme, les physiciens se sont heurtés à une impossibilité d'évaluer ces « champs résiduels » jusqu'à la détermination de leur valeur moyenne hν/2 par mode monochromatique, à 0K, faite par Planck et Nernst. La théorie de l'émission et de l'absorption due à Einstein (1917) a été complétée par l'interprétation de l'émission spontanée de lumière comme une amplification du champ résiduel. Le sens d'échange d'énergie entre une source monochromatique et le champ dépend de l'interférence du champ émis avec le champ d'origine extérieure préexistant dans le mode, donc simplement des phases relatives.
Le champ résiduel dans un corps noir à 0K, habituellement nommé « champ du point zéro », est souvent présenté comme un champ mystérieux d'origine quantique, présentation absurde puisque sa valeur moyenne a été correctement évaluée par Nernst plus de dix ans avant la naissance de la mécanique quantique ; sans sa connaissance il n'aurait pas été possible de fonder l'électrodynamique quantique en identifiant l'énergie électromagnétique d'un mode à celle d'un oscillateur harmonique quantique.
Il faut se garder de penser que dans un mode il y a deux champs, un champ usuel et un champ du point zéro ; une telle conception serait absurde puisque le champ dans un mode dépend d'un seul paramètre réel, l'amplitude du champ.
Ainsi, une absorption d'un mode ne peut réduire l'amplitude du champ que jusqu'à une limite inférieure qui correspond, en moyenne, à l'énergie hν/2 ; une émission est une amplification d'un champ préexistant ; elle est dite spontanée si le champ préexistant correspond à une énergie voisine de hν/2, et induite si cette énergie est notablement supérieure à hν/2.
Quantification en électrodynamique classique.
Un système physique possède, en général, des minimums d'énergie relatifs. En régime non évolutif (stationnaire), le système, excité par un champ électromagnétique de l'ordre de hν/2 dans chaque mode qu'il est susceptible d'émettre (donc d'absorber), reste au voisinage d'un minimum d'énergie ; pour chaque mode monochromatique, son excitation l'amène à rayonner un champ en quadrature avec le champ incident, ce qui ne produit aucun échange d'énergie permanent, mais introduit un retard, la réfraction. Pour un champ plus intense, en particulier en raison d'une fluctuation favorable du champ, le système peut franchir un col de son diagramme d'énergie et absorber une énergie hν cette absorption peut conduire à un niveau peu stable d'où le système peut évoluer rapidement vers d'autres niveaux, en une cascade plus ou moins radiative qui l'amène à un état stationnaire, stable.
Dans une théorie classique, aucun paradoxe ne peut être admis, en particulier le paradoxe d'Einstein, Podolsky et Rosen n'existe pas : supposons qu'un atome perde une énergie de résonance hν, par exemple par le rayonnement d'un dipôle. Le mode d'émission de ce dipôle n'est pas orthogonal aux modes d'émission (donc d'absorption) d'autres atomes dont l'amplitude peut être accrue ; 0, 1, 2, ... atomes peuvent alors absorber hν, même si, en moyenne, un seul atome est excité ; les champs résiduels jouent le rôle d'un bain thermodynamique.
Quelques erreurs habituelles
Il a été écrit que l'électron d'un atome d'hydrogène suivant une orbite de Bohr émet un champ, donc rayonne de l'énergie et devrait tomber sur le noyau. L'électron émet bien un champ, mais d'énergie très faible en raison de l'interférence du champ émis avec le champ résiduel ; cette énergie tombe à zéro si l'orbite est légèrement corrigée, de sorte que l'énergie de l'état stationnaire subit le déplacement de Lamb.
L'étude de l'amorçage d'un laser semble indiquer que le champ du point zéro induit une émission deux fois plus intense qu'un champ d'intensité plus grande. Pour tenir compte de ce résultat, on peut introduire une « radiation de réaction », ad hoc. La véritable explication est très simple : un atome est excité par un champ dans le mode qu'il peut émettre, dit sphérique ; au démarrage du laser, il existe dans ce mode une amplitude correspondant à hν/2 ; le laser fonctionne sur un mode d'onde plane dont il faut prendre la composante sphérique pour exciter l'atome, ce qui divise l'énergie par deux.
Il n'existe pas de système électromagnétique isolé ; oublier que le champ minimum est le champ du point zéro conduit à des erreurs lorsqu'on détecte des champs faibles.
Formulation covariante
NB Cette partie suit les conventions de signe classiques de MTW [6]
Cette partie adopte également la convention de sommation d'Einstein.
Géométrie de l'espace-temps de Minkowski
L'espace-temps de Minkowski (1908) est une variété différentielle M plate munie d'une métrique lorentzienne.
Soit un système de coordonnées quelconque xμ autour d'un évènement (point) P de l'espace-temps, et soient
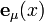 une base locale de TxM, espace tangent à la variété au point
une base locale de TxM, espace tangent à la variété au point 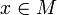 . Un vecteur tangent
. Un vecteur tangent 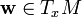 s'écrit alors comme la combinaison linéaire :
s'écrit alors comme la combinaison linéaire :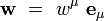
Les wμ sont appelée les composantes contravariantes du vecteur w. Le tenseur métrique
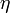 est la forme bilinéaire symétrique[7] :
est la forme bilinéaire symétrique[7] :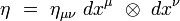
Dans une base orthonormée d'un référentiel inertiel, ses composantes covariantes ημν sont :
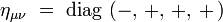
Ses composantes contravariantes ημν vérifient :
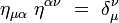
On obtient explicitement :
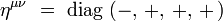
On utilisera ci-dessous les conventions usuelles suivantes :
- un indice grec varie de 0 à 3. Il est associé à une grandeur dans l'espace-temps.
- un indice latin varie de 1 à 3. Il est associé aux composantes spatiales d'une grandeur dans l'espace-temps.
Par exemple, les composantes contravariantes du 4-vecteur position s'écrivent dans un système de coordonnées orthonormales :
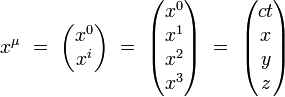
Le tenseur métrique définit pour chaque point
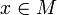 de l'espace-temps un pseudo-produit scalaire (pseudo au sens où l'hypothèse de positivité est retirée) dans l'espace TxM euclidien tangent à M au point x. Si
de l'espace-temps un pseudo-produit scalaire (pseudo au sens où l'hypothèse de positivité est retirée) dans l'espace TxM euclidien tangent à M au point x. Si 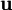 et
et 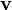 sont deux vecteurs de TxM, leur produit scalaire s'écrit :
sont deux vecteurs de TxM, leur produit scalaire s'écrit :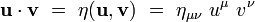
En particulier, en prenant deux vecteurs de base, on obtient les composantes :
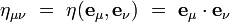
wμ désignant les composantes contravariantes du vecteur w, on peut définir de même ses composantes covariantes par :
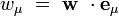
Par exemple, les composantes covariantes du 4-vecteur position s'écrivent dans un système de coordonnées orthonormales :
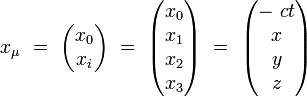
Quadri-gradient
On introduit l'opérateur différentiel quadri-gradient par ses composantes covariantes :
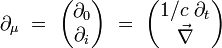
Ses composantes contravariantes s'écrivent :
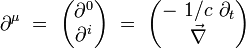
L'opérateur invariant d'Alembertien s'écrit par exemple :
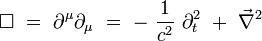
Quadri-potentiel
On introduit le quadri-potentiel électromagnétique par ses composantes contravariantes :
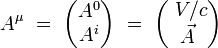
où V est le scalaire potentiel électrique, et
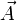 le potentiel-vecteur magnétique. Ses composantes covariantes s'écrivent :
le potentiel-vecteur magnétique. Ses composantes covariantes s'écrivent :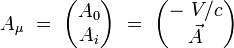
Les lois de transformation de jauge écrite précédemment sont donc résumées dans cette notation sous la forme
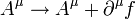
La condition de jauge de Lorenz s'écrit par exemple de façon covariante :
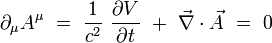
Quadri-courant
On introduit le quadri-courant électromagnétique par ses composantes contravariantes :
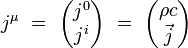
où ρ est le scalaire densité électrique de charge, et
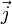 le vecteur densité de courant. Ses composantes covariantes s'écrivent :
le vecteur densité de courant. Ses composantes covariantes s'écrivent :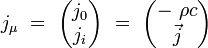
Tenseur de Maxwell
Le tenseur électromagnétique est le tenseur anti-symétrique de rang deux défini à partir du quadri-potentiel par :
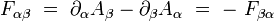
Ses composantes covariantes s'écrivent explicitement :
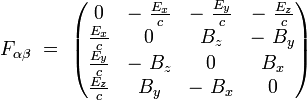
On obtient ses composantes contravariantes en écrivant :
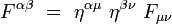
La métrique étant diagonale dans un référentiel inertiel, on obtient alors les formules suivantes, sans sommation sur les indices répétés :
soit explicitement :
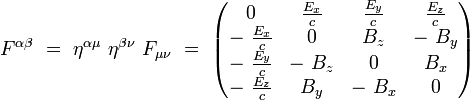
Équations de Maxwell sous forme covariante
Les équations de Maxwell se mettent sous forme relativiste covariante.
- Les deux équations de Maxwell sans termes de sources s'écrivent :
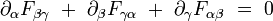
- Les deux équations de Maxwell avec termes de sources s'écrivent :
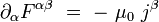
Puisque le tenseur de Maxwell est anti-symétrique, cette dernière relation entraîne en particulier que le quadri-courant est conservé :
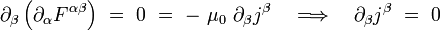
Équation de propagation pour le quadri-potentiel en jauge de Lorenz
En écrivant explicitement le tenseur de Maxwell en termes du quadri-potentiel dans l'équation covariante avec terme de sources, on obtient pour le membre de gauche :
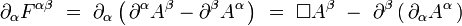
Dans la jauge de Lorenz
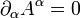 , le second terme disparaît, et l'équation de Maxwell avec terme de sources se réduit à une équation de propagation pour le quadri-potentiel :
, le second terme disparaît, et l'équation de Maxwell avec terme de sources se réduit à une équation de propagation pour le quadri-potentiel :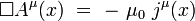
La solution de cette équation s'écrit de façon simple si l'on connaît une fonction de Green de l'équation de propagation, c'est-à-dire une fonction G(x) solution[8] de l'équation aux dérivées partielles :
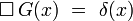
où δ(x) est la distribution de Dirac. On obtient alors le quadri-potentiel sous la forme d'un produit de convolution :
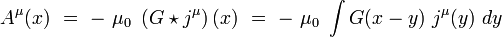
Exemple : les potentiels retardés
En électrodynamique classique, on utilise le plus souvent la fonction de Green retardée qui satisfait à l'hypothèse de causalité :
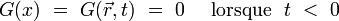
Équations de Maxwell-Lorentz dans les milieux matériels
Liens internes
- Vecteur de Poynting
- Établissement de l'équation de propagation à partir des équations de Maxwell
- Électrodynamique des milieux continus
- Invariance de Lorentz
- Champ de Maxwell
Bibliothèque virtuelle
- Ruth Durrer ; Electrodynamique II (PostScript) : cours approfondi donné par l'auteur (Département de Physique Théorique, Université de Genève, Suisse) aux étudiants de deuxième année de premier cycle (123 pages).
- Jean-Michel Raimond ; [pdf]Electromagnétisme & relativité restreinte : cours approfondi (mécanique analytique, relativité & électromagnétisme) donné par l'auteur (laboratoire Kastler-Brossel, ENS Ulm, Paris) aux étudiants de première année du Magistère Interuniversitaire de Physique.
Bibliographie
Cours
Ouvrages d'introduction
Accessible au niveau du premier cycle universitaire.
- Richard P. Feynman ; Le cours de physique de Feynman, InterEditions (1979). Le grand théoricien de l'électrodynamique quantique, prix Nobel 1965, nous donne ici un superbe cours d'introduction à l'électromagnétisme classique. Publié en deux volumes :
- Electromagnétisme I, ISBN 2-7296-0028-0. Réédité par Dunod, ISBN 2-10-004861-9.
- Electromagnétisme II, ISBN 2-7296-0029-9. Réédité par Dunod, ISBN 2-10-004316-1.
Ouvrages de références
- John D. Jackson ; Électrodynamique classique - Cours et exercices d'électromagnétisme, Dunod (2001), ISBN 2-10-004411-7. Traduction française de la 3e édition du grand classique américain.
- Lev Landau & Evguéni Lifchitz ; Cours de physique théorique - Tome 2 : Théorie des champs, Mir (4e édition-1989), ISBN 5-03-000641-9.
- Wolfgang K. H. Panofsky et Melba Phillips ; Classical electricity and magnetism, Addison-Wesley (2e édition-1962). Réédité par : Dover Publications, Inc. (2005), ISBN 0-486-43924-0. L'ouvrage de référence en électrodynamique classique avant la parution du Jackson
Aspects historiques
- James Clerk Maxwell ; Traité d'Électricité et de Magnétisme, Gauthier-Villars, tome I (1885) et tome II (1887). Réédité par Jacques Gabay (1989), ISBN 2-87647-045-4.
- Hendrik-Antoon Lorentz ; The Theory of Electrons and its Applications to the Phenomena of Light and Radiant Heat - A Course of Lectures delivered in Columbia University, in March and April 1906, B.G. Teubner (Leipzig - 2e édition : 1916). Réédité par Jacques Gabay (1992), ISBN 2-87647-130-2.
- Olivier Darrigol ; Les équations de Maxwell - de MacCullagh à Lorentz, Belin (2005), ISBN 2-7011-3073-5. Historien des sciences, Olivier Darrigol est chercheur au CNRS. Les équations de Maxwell, véritable monument scientifique, fournissent une description précise de l’ensemble des phénomènes électromagnétiques. Bien que James Clerk Maxwell ait joué le rôle le plus éminent dans leur introduction, elles sont apparues dans des contextes divers sous la plume de plusieurs auteurs (MacCullagh, Maxwell et Lorenz) et n’ont acquis leur interprétation moderne que grâce aux efforts d’héritiers de Maxwell (Heaviside, Hertz et Lorentz). C’est ce que montre l’auteur, à travers l’étude détaillée de textes fondateurs écrits dans les deux derniers tiers du XIXe siècle.
- Edmund T. Whittaker (Sir) ; A History of the Theories of Aether and Electricity, Springer Verlag/A.I.P. Press (1986) ISBN 0-88318-523-7, réédité par Dover (1990) ISBN : 0-48626-126-3. Le premier volume (Part I : the classical theories, from the age of Descartes to the close of the nineteenth century) de cette histoire érudite a été publié à Dublin en 1910. Le second volume complémentaire (Part II : the modern theories 1900-1926) est quant à lui paru en 1953. Ce livre essentiel est malheureusement aujourd'hui épuisé. Whittaker, mathématicien appliqué, est également co-auteur(avec G.N. Watson) du très célèbre et indémodable cours d'analyse : A Course of Modern Analysis (Cambridge University Press) paru initialement en 1902.
- Olivier Darrigol ; Electrodynamics from Ampère to Einstein, Oxford University Press (2000) ISBN 0-19-850593-0. Volta invente la pile électrique en 1800. Cette découverte capitale va initier un nouveau champ de recherche : l'électrodynamique, initialement science des courants circulants dans les fils, par opposition aux phénomènes électrostatique des charges fixes connus depuis l'Antiquité. La première loi fondamentale de cette électrodynamique est établie par Ampère en 1820 : il s'agit de la loi de force qui s'exerce entre deux fils parcourus chacun par un courant. Cette histoire de l'électrodynamique détaille le chemin parcouru entre cette loi d'Ampère de 1820 et le triomphe de la théorie des champs de Maxwell-Lorentz-Faraday avec son interprétation par Einstein en 1905 dans le cadre de la théorie de la relativité restreinte. Historien des sciences, Olivier Darrigol est chercheur au CNRS.
- John D. Jackson & L.B. Okun ; Historical roots of gauge invariance, Review of Modern Physics 73 (2001) 663-680. Texte complet disponible sur l'ArXiv : hep-ph/0012061.
Notes et références
- ↑ Pour calculer explicitement le champ électrique, le théorème de Gauss n'est utilisable que dans des cas simples, possédants une « haute » symétrie : symétries sphérique, cylindrique et plane. Il est alors possible de calculer explicitement le flux du champ à travers une surface de Gauss Σ possédant la même symétrie.
- ↑ Certaines théories quantiques modernes de l'unification des interactions fondamentales prédisent l'existence de monopôles magnétiques, mais ces objets n'ont à ce jour jamais été observés. Par ailleurs, Dirac a montré en 1930 comment l'existence d'un monopôle magnétique pourrait expliquer de façon élégante la quantification de la charge électrique observée expérimentalement. Pour une revue de l'« état de l'art » actuel, lire par exemple Kimball A. Milton, Theoretical and experimental statut of magnetic monopoles, Report on Progress in Physics 69 (2006), 1637-1711.
- ↑ Localement signifie ici dans un voisinage de chaque point
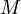 de l'espace physique. Le problème de savoir si on peut définir globalement un potentiel-vecteur sur un espace donné conduit à devoir se poser des questions sur la cohomologie de cet espace, un concept issu de la géométrie différentielle.
de l'espace physique. Le problème de savoir si on peut définir globalement un potentiel-vecteur sur un espace donné conduit à devoir se poser des questions sur la cohomologie de cet espace, un concept issu de la géométrie différentielle. - ↑ Localement signifie : dans le voisinage de chaque point
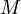 de l'espace physique. Le problème de savoir si on peut définir globalement un potentiel-vecteur sur un espace donné conduit à devoir se poser des questions sur la cohomologie de cet espace, un concept issu de la géométrie différentielle.
de l'espace physique. Le problème de savoir si on peut définir globalement un potentiel-vecteur sur un espace donné conduit à devoir se poser des questions sur la cohomologie de cet espace, un concept issu de la géométrie différentielle. - ↑ Y. Aharonov & D. Bohm ; Significance of electromagnetic potentials in quantum theory, Physical Review 115 (1959), 485–491.
- ↑ C. W. Misner, Kip S. Thorne & John A. Wheeler ; Gravitation, Freeman & Co. (San Francisco-1973), ISBN 0-7167-0344-0.
- ↑ Dans cette formule, dxμ désigne la base duale de
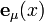 dans l'espace cotangent
dans l'espace cotangent 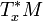 , c'est-à-dire la forme linéaire sur TxM telle que :
, c'est-à-dire la forme linéaire sur TxM telle que :
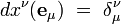
- ↑ Il existe potentiellement plusieurs fonctions de Green pour cette équation, différentes l'une de l'autre par les conditions aux limites choisies. En électrodynamique classique, on utilise le plus souvent la fonction de Green retardée.
- Portail de la physique
- Portail de l’électricité et de l’électronique
Catégories : Électromagnétisme | Outils théoriques de l'électromagnétisme | Équation aux dérivées partielles
Wikimedia Foundation. 2010.