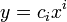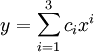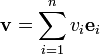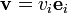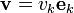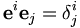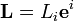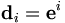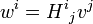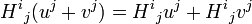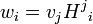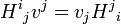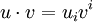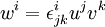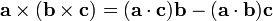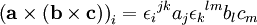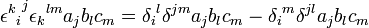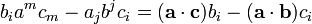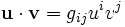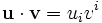Convention De Sommation D'Einstein

Convention de sommation d'Einstein

Articles scientifiques
sur les tenseurs

Généralités

Mathématiques

Tenseur (mathématiques)
Produit tensoriel
... de deux modules
... de deux applications linéaires
Algèbre tensorielle
Champ tensoriel
Espace tensoriel

Physique

Convention d'Einstein
Tenseur métrique
Tenseur énergie-impulsion
Tenseur de Riemann
... de Ricci
... d'Einstein
... de Weyl
... de Levi-Civita
... de Killing
... de Killing-Yano
... de Bel-Robinson
... de Cotton-York
Tenseur électromagnétique
Tenseur des contraintes
Tenseur des déformations

Sommaire

1 Définitions
2 Algèbre vectorielle élémentaire et algèbre matricielle
- 2.1 Exemple
3 Cas sans produit interne

Définitions

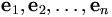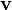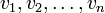Traditionnellement, on s'intéresse à un espace vectoriel V de dimension finie n et une base sur V. On peut écrire les vecteurs de base ainsi: $\mathbf{e}_1, \mathbf{e}_2, \dots, \mathbf{e}_n$ . Dans ce cas, si $\mathbf{v}$ est un vecteur dans V, ces coordonnées dans cette base sont $v_1, v_2, \dots, v_n$ .

La règle de base est :

$\mathbf{v} = \sum_{i=1}^n v_i \mathbf{e}_i$

Qui, avec la convention de sommation d'Einstein, s'écrit

$\mathbf{v} = v_i \mathbf{e}_i$

Dans cette expression on sous-entend que le terme de droite est additionné pour toutes les valeurs de i allant de 1 à n, car l'indice i apparaît deux fois.

L'indice i est dit muet car le résultat ne dépend pas de lui. Par exemple, pour exprimer la même chose on pourrait aussi écrire :

$\mathbf{v} = v_k \mathbf{e}_k$

Dans les contextes dans lesquels l'indice doit apparaître une fois en bas et une fois en haut, les vecteurs de base s'écrivent 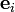$\mathbf{e}_i$ mais les coordonnées s'écrivent $v i$ . La règle de base s'écrit alors :

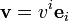$\mathbf{v} = v^i \mathbf{e}_i$ .

L'intérêt de la notation d'Einstein est qu'elle s'applique à d'autres espaces vectoriels construits à partir de V en utilisant le produit tensoriel et la dualité. Par exemple, 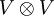$V \otimes V$ , le produit tensoriel de V par lui-même, a une base constituée de tenseurs de la forme 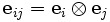$\mathbf{e}_{ij} = \mathbf{e}_i \otimes \mathbf{e}_j$ . Tout tenseur $T$ dans 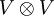$V \otimes V$ peut s'écrire :

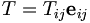$T = T_{ij} \mathbf{e}_{ij}$ .

V*, le dual de V, a une base 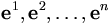$\mathbf{e}^1, \mathbf{e}^2, \dots, \mathbf{e}^n$ qui obéit à la règle :

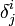$\mathbf{e}^i \mathbf{e}_j = \delta^i_j$

où $\delta^i_j$ est le symbole de Kronecker : 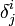$\delta^i_j$ vaut 1 si i = j et 0 sinon.

Ici nous avons utilisé un indice inférieur pour la base duale, comme c'est le cas lorsque les indices doivent apparaître une fois en haut et une fois en bas. Dans ce cas, si 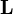$\mathbf{L}$ est un élément de V*, alors :

$\mathbf{L} = L_i \mathbf{e}^i$

Si au contraire, tous les indices doivent être placés en base, alors une lettre différente doit être utilisée pour désigner la base duale. Par exemple:

$\mathbf{d}_i = \mathbf{e}^i$

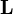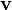L'utilité de la notation d'Einstein apparaît surtout dans les formules et les équations qui ne font pas mention de la base choisie. Par exemple, avec $\mathbf{L}$ et $\mathbf{v}$ défini comme plus haut :

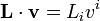$\mathbf{L}\cdot\mathbf{v} = L_i v^i$ .

Et ceci est vrai pour toutes les bases.

Les sections suivantes contiennent d'autres exemples de telles équations.

Algèbre vectorielle élémentaire et algèbre matricielle

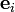Soit V un espace vectoriel dans $\mathbb{R}^n$ , alors il existe un base standard pour V dans laquelle $\mathbf{e}_i$ est (0,...,0,1,0,...,0), avec le 1 à la position i. Dans ce cas, les matrices n × n peuvent être vues comme des éléments de 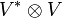$V^* \otimes V$ . On peut aussi considérer les vecteurs dans V comme des vecteurs colonnes ou comme des matrices n × 1 et les éléments de V* comme des vecteurs rangées ou des matrices 1 × n.

Dans les exemples qui suivent, tous les indices apparaîtront en position haute. C'est parce que V a un produit interne et que la base base choisie est orthonormale, comme cela est expliqué dans la section suivante.

Si H est une matrice et b est un vecteur colonne, alors Hb est un autre vecteur colonne. Pour définir w = Hb, on peut écrire:

$w^i = {H^i}_j v^j \,$

L'indice muet j apparaît deux fois dans le terme de droite, tandis que i apparaît une seule fois dans chaque terme.

En utilisant la distributivité, 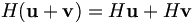$H (\mathbf{u} + \mathbf{v}) = H \mathbf{u} + H \mathbf{v}$ peut s'écrire:

${H^i}_j (u^j + v^j) = {H^i}_j u^j + {H^i}_j v^j \,$

Cet exemple montre la preuve de la loi de distributivité, car l'équation des indices ne fait que directement référence aux nombres réels 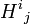${H^i}_j$ , $u j$ et $v j$ et sa validité découle directement de celle de la distributivité de ces nombres.

La transposée d'un vecteur colonne est un vecteur ligne avec les mêmes composantes et la transposée d'une matrice est une autre matrice dont les composantes sont données en inversant les indices. Supposons que nous sommes intéressés par 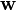$\mathbf{w}$ , le produit de 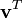$\mathbf{v}^T$ par $H T$ . Alors:

$w_i = v_j {H^j}_i \,$

Donc pour exprimer que la transposée d'un produit inverse l'ordre de la multiplication, nous pouvons écrire:

${H^i}_j v^j = v_j {H^j}_i \,$

À nouveau, ceci découle directement de la commutativité des nombres réels.

Le produit scalaire de deux vecteurs u et v peut s'écrire:

$u \cdot v = u_i v^i \,$

Si n = 3, nous pouvons aussi écrire le produit vectoriel en utilisant le symbole de Levi-Civita. Par exemple, si w est u × 'v, alors:

$w^i = \epsilon^i_{jk} u^j v^k \,$

Ici le symbole de Levi-Civita $ε i j k$ est le tenseur totalement anti-symétrique tel que $ε 123 = 1$ . Concrètement :

$ε i j k = 1$ si $(i, j, k)$ est une permutation paire de $(1,2,3)$ ;
$ε i j k = - 1$ si $(i, j, k)$ est une permutation impaire de $(1,2,3)$ ;
$ε i j k = 0$ si $(i, j, k)$ n'est pas une permutation de $(1,2,3)$ (s'il y a deux fois le même indice).

Exemple

Article principal : Identités vectorielles.

Soit à démontrer l'identité vectorielle suivante :

$\mathbf a \times (\mathbf b \times \mathbf c) = (\mathbf a \cdot \mathbf c)\mathbf b - (\mathbf a \cdot \mathbf b)\mathbf c$

Avec a b et c des vecteurs quelconques. En notation d'Einstein, on a :

$\left(\mathbf a \times (\mathbf b \times \mathbf c)\right)_i = {\epsilon_i}^{jk} a_j {\epsilon_k}^{lm}b_lc_m$

En réarrangeant les termes et en permutant les indices, on obtient l'expression équivalente suivante :

${{{\epsilon}^k}_i}^j {\epsilon_k}^{lm}a_j b_lc_m = {\delta_i}^{l}{\delta^{jm}}a_j b_lc_m - {\delta_i}^{m}{\delta^{jl}}a_j b_lc_m$

En utilisant les propriétés du symbole de Levi-Civita. On a alors en réorganisant et en simplifiant les termes :

$b_i a^m c_m - a_j b^j c_i = (\mathbf a \cdot \mathbf c)b_i - (\mathbf a \cdot \mathbf b)c_i$

On a donc finalement :

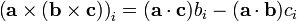
$\left(\mathbf a \times (\mathbf b \times \mathbf c)\right)_i = (\mathbf a \cdot \mathbf c)b_i - (\mathbf a \cdot \mathbf b)c_i$

En explicitant l'indice i, on retrouve l'identité.

Cas sans produit interne

Dans les exemples ci-dessus, vous pouvez remarquez que les formules sont toujours valides si les indices muets sont présents une fois comme indice supérieur et une fois comme indice inférieur, sauf dans l'exemple concernant la transposée. C'est parce que ces exemples utilisent implicitement le produit interne dans un espace euclidien (produit scalaire) alors que l'exemple avec le transposée ne le fait pas.

Dans certaines applications, il n'y a pas de produit interne sur V. Dans ces cas, requérir que les indices muets doivent apparaître une fois en haut et une fois en bas peut aider à éviter des erreurs, un peu comme l'analyse dimensionnelle permet d'éviter les erreurs d'unités. Plus significativement, le produit interne peut être l'objet principal de l'étude et ne devrait pas être supprimé de la notation; c'est le cas, par exemple, des équations de la relativité générale. Dans ces cas, la différence entre la position d'un indice peut-être cruciale.

Quand on se réfère explicitement au produit interne, ces composantes sont souvent notées : $g i j$ (cfr. tenseur métrique). On notera que $g i j = g j i$ . La formule pour le produit scalaire devient alors:

$\mathbf{u} \cdot \mathbf{v} = g_{ij} u^i v^j$

On peut aussi abaisser l'indice en définissant:

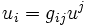$u_i = g_{ij} u^j \,$ ,

ce qui donne:

$\mathbf{u} \cdot \mathbf{v} = u_i v^i$

Ici, nous avons implicitement utilisé le fait que $g i j = g j i$ .

De façon similaire, nous pouvons élever un indice en utilisant le produit interne correspondant sur V*. Le produit interne est alors défini par $g i j$ , qui en tant que matrice est l'inverse de $g i j$ . Si vous élevez un indice puis l'abaissez (ou le contraire), vous retrouvez ce que aviez au départ. Si vous élevez le i dans $g i j$ , alors vous obtenez 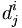$d^i_j$ et si vous élevez le j dans 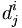$d^i_j$ vous obtenez $g i j$ .

Si la base choisie pour V est orthonormale, alors $g i j = g i j$ et $u i = u i$ . Dans ce cas, on retrouve la formule pour le produit scalaire de la section précédente. Mais si la base n'est pas orthonormale, cela ne sera plus vrai. Donc si vous étudiez le produit interne et que vous ne pouvez pas savoir si la base est orthonormale, vous devrez vous référez explicitement à $g i j$ . De plus, si le produit interne n'est pas défini-positif, comme c'est le cas en relativité générale, $g i j = d j i$ ne sera pas vrai même si la base est orthonormale car vous aurez parfois -1 au lieu de 1 quand i = j.

Portail de la physique

Ce document provient de « Convention de sommation d%27Einstein ».

Catégories : Tenseur | Albert Einstein | Relativité générale

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Convention De Sommation D'Einstein de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Convention de sommation d'einstein — Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel Espace tensoriel … Wikipédia en Français
Convention de sommation d’Einstein — Convention de sommation d Einstein Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel… … Wikipédia en Français
Convention de sommation d'Einstein — En mathématiques et plus spécialement dans les applications de l algèbre linéaire en physique, la convention de sommation d Einstein ou notation d Einstein est un raccourci de notation utile pour la manipulation des équations concernant des… … Wikipédia en Français
Convention d'Einstein — Convention de sommation d Einstein Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel… … Wikipédia en Français
Einstein (Homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. L einstein est une unité de mesure correspondant à l énergie lumineuse absorbée par une mole de réactif. Personnes Albert Einstein est le célèbre… … Wikipédia en Français
Einstein (homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. L einstein est une unité de mesure correspondant à l énergie lumineuse absorbée par une mole de réactif. Personnes Albert Einstein est le célèbre… … Wikipédia en Français
Einstein — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. L einstein est une unité de mesure correspondant à l énergie lumineuse absorbée par une mole de réactif. Personnes Albert Einstein est le célèbre… … Wikipédia en Français
Notation d'Einstein — Convention de sommation d Einstein Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel… … Wikipédia en Français
Tenseur d'Einstein — En relativité générale, le tenseur d Einstein est la quantité qui décrit comment le champ gravitationnel est affecté par la présence de matière. Sommaire 1 Formule du tenseur d’Einstein en deux dimensions 2 Propriété fondamentale 3 … Wikipédia en Français
Identités vectorielles — Les identités suivantes peuvent être utiles en analyse vectorielle … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Convention De Sommation D'Einstein