- Automatique
-
 Pour les articles homonymes, voir Automatic.
Pour les articles homonymes, voir Automatic.L’automatique fait partie des sciences de l'ingénieur. Cette discipline traite de la modélisation, de l’analyse, de la commande et, de la régulation des systèmes dynamiques. Elle a pour fondements théoriques les mathématiques, la théorie du signal et l’informatique théorique. L’automatique permet de contrôler un système de manière continue et en respectant un cahier des charges (rapidité, dépassement, stabilité …).
Les hommes de l'art en automatique se nomment automaticiens.
Un exemple simple est celui du régulateur de vitesse d’une automobile, il permet de maintenir le véhicule à une vitesse constante prédéterminée par le conducteur, indépendamment des perturbations (pente de la route, résistance du vent...).
On dit que l’automatique permet la réalisation d’asservissements, à ne pas confondre avec les automatismes, ces derniers étant à évènements discrets et non continus. Les systèmes automatisés peuvent contenir à la fois des automatismes et des asservissements.
Sommaire
Histoire de l'automatique
Généralités, concepts
On souhaite contrôler la température d’un four. La première tâche consiste à définir le système « four ». Celui-ci possède une entrée (le courant fourni à la résistance de chauffage) et une sortie (la température à l’intérieur du four). On modélise le système sous forme d’équations, qui permettent d’exprimer les relations entre les entrées et les sorties du système, sous la forme d’une équation différentielle ou d’une fonction de transfert. On détermine aussi les conditions de stabilité du système (on ne veut pas que le four se mette à augmenter la température sans s’arrêter).
Les personnes chargées de réguler ce système ont un cahier des charges à respecter:
- la stabilité (le régulateur ne doit pas rendre le système instable),
- la poursuite (la température du four doit atteindre la température en consigne, on peut spécifier dans le cahier des charges si on a des contraintes de rapidité ou de dépassement),
- le rejet des perturbations (on ouvre la porte du four, la température descend, la température doit rejoindre la température voulue).
- Les coûts et délais de développement.
Après avoir déterminé la solution répondant le mieux aux besoins, on va synthétiser un nouveau système, le « régulateur », celui-ci aura pour entrées la consigne (c’est-à-dire la température souhaitée à l’intérieur du four) ainsi que la température réelle du four fourni par un capteur et pour sortie la commande du four, cette sortie est ainsi reliée à l’entrée du système four.
L’ensemble forme ce qu’on appelle un « système asservi ».
Le régulateur peut alors être réalisé sous forme analogique (circuit électronique) ou numérique (microcontrôleur). Il existe également des régulateurs dans le commerce qui permettent ces fonctions, où l’automaticien peut choisir la méthode de régulation, ou par exemple entrer les coefficients dans le cadre d’un régulateur Proportionnel-Intégral-Dérivé.
À propos des systèmes
Un système est une modélisation d’un procédé en fonctionnement. Il possède une ou plusieurs entrées, et une ou plusieurs sorties. Les entrées du système sont appelées variables exogènes, qui rassemblent les perturbations et les variables manipulées, commandes ou grandeurs de réglage. Elles sont souvent représentées de manière générique par la lettre u ou e. Elles sont reliées au procédé en tant que tel par un capteur.
Les sorties du système sont appelées variables contrôlées, mesures ou grandeurs réglées. Elles sont souvent représentées de manière générique par la lettre y. Le procédé est relié à la sortie du système par un actionneur.
Dans le cas d’un système échantillonné, les entrées et sortie sont à temps discret, mais le système en-lui même demeure à temps continu. Le système inclut donc un convertisseur numérique-analogique en entrée, un convertisseur analogique-numérique en sortie et une horloge permettant de fixer la fréquence d'échantillonnage.
Il existe une infinité d’exemples de systèmes : des systèmes mécaniques, des systèmes électriques ou des procédés chimiques. La représentation du système ne pourra alors se faire qu’avec de bonnes connaissances dans le domaine physique correspondant.
Différents systèmes
Les systèmes peuvent être classés en plusieurs catégories.
Systèmes à temps continu, à temps discret
- Systèmes à temps continus : ce sont les systèmes qui existent naturellement.
- Systèmes à temps discrets : ce sont des systèmes dont le temps a été discrétisé. Ces systèmes n'existent pas à l’état naturel (la majorité des systèmes physiques naturels sont de type à temps continu), mais étant donné que la plupart des contrôleurs utilisés en automatique sont calculés par des processeurs numériques, il est parfois intéressant de modéliser le système commandé comme un système à temps discret.
- Systèmes à évènements discrets : systèmes dont le fonctionnement peut être modélisé par des évènements discrets. Généralement, ces systèmes sont modélisés par des réseaux de Petri, ou par les algèbres de dioïdes. Des exemples sont les réseaux ferroviaires, ou le fonctionnement d’une chaîne de montage.
- Systèmes hybrides : systèmes dont la modélisation nécessite l’utilisation des techniques liées aux systèmes continus et aux systèmes à évènements discrets, par exemple : une boîte de vitesse de voiture.
Systèmes monovariables, systèmes multivariables
Quatre possibilités existent:
- le système a une entrée et une sortie, c’est un système monovariable ou SISO (Single Input Single Output),
- le système a plusieurs entrées et plusieurs sorties, c’est un système multivariable ou MIMO (Multiple Input Multiple Output),
- le système a une entrée et plusieurs sorties, système SIMO,
- le système a plusieurs entrées et une sortie, système MISO.
Système invariant
Ce sont des systèmes dont les paramètres du modèle mathématique ne varient pas au cours du temps.
Systèmes linéaires ou non linéaires
Article détaillé : Système linéaire.On dit qu’un système est linéaire s'il est régit par un système d'équations différentielles à coefficients constants .
Aucun système n’est strictement linéaire, ne serait-ce que par les saturations (butées physiques, par exemple) qu’il comporte ou encore par les phénomènes d’hystérésis.
Inversement, un système non-linéaire peut parfois être considéré comme linéaire dans une certaine plage d’utilisation. Il faut toujours garder à l’esprit que le système sur lequel on peut travailler n’est qu’un modèle mathématique de la réalité, et que par conséquent il y a une perte d’information lors du passage au modèle. Bien sûr, il incombe à l’ingénieur de juger la pertinence de son modèle vis-à-vis des objectifs fixés.
Représentation des systèmes linéaires invariants
Les automaticiens ont l’habitude de représenter graphiquement un système asservi par l’utilisation de schémas fonctionnels.
Équation différentielle et fonction de transfert
Article détaillé : Fonction de transfert.Un système physique se décrit généralement avec des équations différentielles (principe fondamental de la dynamique, caractéristique d’un condensateur ou d’une bobine…). La transformée de Laplace permet alors de passer de l’équation différentielle à une fonction de transfert.
Pour un système à temps discret on utilise la transformée en Z.
Cette fonction permettra de déduire le comportement entrée-sortie du système.
Représentation temporelle
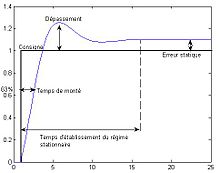
Articles détaillés : Réponse impulsionnelle et Réponse indicielle.On peut s’intéresser au comportement du système lorsqu’on le soumet à certains signaux comme une impulsion de Dirac ou un échelon. On peut en déduire un certain nombre de caractéristiques du système.
Représentation fréquentielle
Le diagramme de Bode représente, sur des graphes séparés, le gain et la phase en fonction de la fréquence.
Le diagramme de Nyquist représente la partie imaginaire de la fonction de transfert en fonction de la partie réelle.
Le diagramme de Black représente le gain en fonction de la phase.
Représentation d’état
Article détaillé : Représentation d'état.La représentation d’état est une représentation matricielle du système. On s'intéresse à des variables internes aux systèmes, appelées variables d’état. On représente alors la dérivée des variables d’état en fonction d’elles-mêmes et de l’entrée, ainsi que la sortie en fonction des variables d'état et de l'entrée.
De cette représentation on peut déduire le comportement entrée-sortie du système (On peut déduire de la représentation d’état la fonction de transfert) mais aussi un certain nombre d'autres informations comme la commandabilité ou l' observabilité.
La représentation d’état peut aussi représenter un système non-linéaire ou un système variant dans le temps.
Stabilité
Dans le cas des systèmes linéaires représentés par une fonction de transfert, l'analyse des pôles permet de conclure sur la stabilité du système. On rappelle que les pôles d'une fonction de transfert sont les complexes p0,p1... qui annulent le dénominateur.
- Dans le cas d'une fonction de transfert continue utilisant la transformée de Laplace, tous les pôles doivent être à partie réelle strictement négative pour que le système soit stable.
- Dans le cas d'une fonction de transfert discrète utilisant la transformée en Z, tous les pôles doivent avoir un module inférieur à 1 pour que le système soit stable.
Attention, en automatique, le terme stabilité doit être défini précisément car il existe une dizaine de sortes de stabilités différentes. En général on fait référence à une stabilité asymptotique.
Dans le cas des systèmes non-linéaires, la stabilité est généralement étudiée à l'aide de la théorie de Lyapunov.
Contrôle en boucle ouverte
Article détaillé : Contrôle en boucle ouverte.Dans de rares cas, le contrôle se fait en boucle ouverte tel un Automate programmable industriel, en tenant compte uniquement de la consigne et non du retour. Cela revient par exemple à conduire une voiture les yeux fermés. On ne parle pas de « système asservi » dans un tel cas.
Asservissement
Article détaillé : Asservissement (automatique).Système bouclé
La technique d'automatisation la plus répandue est le contrôle en boucle fermée. Un système est dit en boucle fermée lorsque la sortie du procédé est prise en compte pour calculer l'entrée. Généralement le contrôleur effectue une action en fonction de l’erreur entre la mesure et la consigne désirée. Le schéma classique d'un système linéaire pourvu d'un régulateur linéaire en boucle fermée est le suivant :
La boucle ouverte du système est composée de deux sous-systèmes : le procédé et le régulateur (ou « correcteur »). La fonction de transfert de ce système en boucle ouverte est donc :

Avec cette architecture on peut recalculer une nouvelle fonction de transfert du système, soit la fonction de transfert en boucle fermée, à l'aide des relations entre les différentes variables :


e(s) = r(s) − y(s)On obtient alors :

La fonction
 représente la fonction de transfert en boucle fermée. On peut remarquer que pour les systèmes à retour unitaire
représente la fonction de transfert en boucle fermée. On peut remarquer que pour les systèmes à retour unitaire : c’est la formule de Black qui permet de passer d’une fonction de transfert en boucle ouverte (à retour unitaire) à une fonction de transfert en boucle fermée.
: c’est la formule de Black qui permet de passer d’une fonction de transfert en boucle ouverte (à retour unitaire) à une fonction de transfert en boucle fermée.Remarques :
- La boucle de retour est le chemin qui part de la sortie et qui revient au comparateur avec le signe "moins". Dans cette boucle, il y a généralement un bloc représentant, dans la plus grande majorité des cas, un capteur. Si ce bloc a comme fonction de transfert "1" (ce qui équivaut à une absence de bloc car la multiplication par 1 ne change rien), on dit que le schéma-bloc est à retour unitaire. La formule précédemment énoncée n'est valable que si le schéma-bloc est à retour unitaire.
- Quel que soit le schéma-bloc (unitaire ou non, avec ou sans perturbation, ...), le dénominateur de la fonction de transfert en boucle fermée est toujours : 1 + HBO(s) avec HBO(s) étant la fonction de transfert en boucle ouverte c'est-à-dire le produit de tous les blocs de la boucle, y compris ceux de la boucle de retour.
L'étude de cette fonction de transfert en boucle fermée permet l'analyse fréquentielle et temporelle du système général avec le contrôleur.Exemple de boucle de régulation
Reprenons l’exemple du moteur automobile.
On le commande en choisissant l'ouverture du papillon des gaz intégré au système d'injection du moteur. L'ouverture est directement liée à la force appliquée sur le piston donc à l’accélération du véhicule. Disons qu’elles sont proportionnelles (on néglige les pertes et la résistance de l’air sur le véhicule).
On veut maintenir une certaine vitesse, 90 km/h par exemple. 90 km/h est la consigne, il faut la comparer à la vitesse réelle donnée par un tachymètre.
La différence donne la variation de vitesse à réaliser. On en déduit l’accélération à demander au véhicule.
Connaissant le rapport entre l’accélération et l'ouverture du papillon, on calcule l'ouverture à donner au papillon pour s’approcher de la vitesse de consigne. Le compteur de vitesse prend alors la nouvelle valeur de la vitesse pour réitérer l’opération. De cette manière, lorsqu’on approche de la vitesse voulue, l’accélération diminue jusqu’à s’annuler sans brutalité.
On obtient donc ce schéma.
En réalité, à cause des pertes, il faut maintenir une certaine accélération entre autres pour lutter contre la résistance de l’air.
Les différentes techniques
Il existe différentes techniques pour synthétiser les régulateurs. La technique industrielle la plus largement utilisée est le régulateur PID qui calcule une action Proportionnelle, Intégrale et Dérivée en fonction de l’erreur consigne/mesure. Cette technique permet de satisfaire la régulation de plus de 90% des procédés industriels. La commande à modèle interne est également répandue.
Des techniques avancées se basent sur la commande par retour d'état (ou commande par retour d'état reconstruit par un observateur). On peut aussi utiliser la commande par placement de pôles souvent appelé régulateur RST.
Autres commandes :
- La Commande LQ
- La Commande LQG
- La H infini
- La commande prédictive se basant sur l'utilisation d'un modèle dynamique du système pour anticiper son comportement futur.
- La commande robuste permettant de garantir la stabilité par rapport aux perturbations et aux erreurs de modèle.
- La commande adaptative qui effectue une identification en temps réel pour actualiser le modèle du système.
- La logique floue utilisant un réseau de neurones ou un système expert.
- Les contrôleurs non linéaires utilisant la théorie de Aleksandr Lyapunov, comme les commandes linéarisantes ou la commande par modes glissants, plus robuste.
- La commande par platitude différentielle, qui permet l'inversion de modèle sans passer par l'intégration des équations différentielles, et ainsi de calculer les signaux nécessaires sur les entrées pour garantir les trajectoires voulues en sortie.
Notes et références de l'article
Liens et documents externes
- Cours d'Actionneurs et effecteurs
- Philippe de Larminat, Automatique appliquée, 2e édition, Hermes, 2009
- Philippe de Larminat, Automatique, commande des systèmes linéaires, Hermes, 2e édition, 1995
- Patrick Prouvost, Automatique Contrôle et régulation, Dunod
- Sandrine Le Ballois, Pascal Codron : Automatique : systèmes linéaires et continus, Dunod
- Hassan K. Khalil, Non linear Systems, Prentice Hall
- Bode, Network analysis and feedback amplifier designer, D. Van Nostrand Company
- Portail de l’électricité et de l’électronique
Wikimedia Foundation. 2010.