- Loi De Biot Et Savart
-
Loi de Biot et Savart
La loi de Biot et Savart, nommé en l'honneur des physicien français Jean-Baptiste Biot et Félix Savart (1820) donne le champ magnétique créé par une distribution de courants continus. Elle constitue l'une des lois fondamentales de la magnétostatique, au même titre que la loi de Coulomb pour l'électrostatique.
Sommaire
Cas d'un circuit filiforme
Un circuit filiforme est une modélisation où le fil électrique est un objet purement linéique. C'est une idéalisation d'un fil réel dont la longueur serait très supérieure aux dimensions transverses de sa surface de section.
Loi de Biot et Savart
Soit C la courbe géométrique représentant le circuit filiforme, et soit r' un point de cette courbe C. On note dl le vecteur déplacement élémentaire tangent à la courbe C' au point r'. Dans le vide, le circuit parcouru par un courant continu d'intensité I crée en tout point r extérieur à C le champ magnétique B(r) donné par la formule
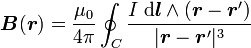 ,
,
où μ0 est une constante fondamentale, appelée perméabilité magnétique du vide.
Remarque sur une notation
On dit parfois que l'« élément infinitésimal » de longueur dl, situé au point r' et parcouru par le courant I crée le « champ magnétique élémentaire » dB au point r, où
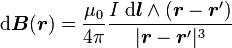 .
.
Il importe de bien comprendre qu'il s'agit là d'un abus de langage mathématiquement commode pour poser le paramétrage de l'intégrale. En effet, le courant d'intensité I ne peut circuler que dans le circuit fermé complet C, et seule l'intégrale complète possède un sens physique.
Autres modélisations
Densité surfacique de courant
Dans le cas d'une densité surfacique de courant jS existant sur la surface Σ, le champ magnétique créé s'écrit
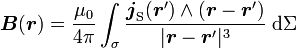 .
.
Densité volumique de courant
Dans le cas d'une densité surfacique de courant j existant sur tout un volumela surface Σ, le champ magnétique créé s'écrit
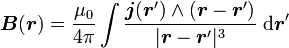 .
.
Théorème d'Ampère
En intégrant la loi de Biot et Savart sur une boucle fermée Γ quelconque (qui a priori n'est pas un circuit électrique), on démontre le théorème d'Ampère :
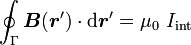 ,
,
où Iint est l'intensité algébrique enlacée par la courbe Γ.
Le cas d'une particule chargée
En remarquant qu'une particule ponctuelle située en r', de charge électrique q animée d'une vitesse v correspond à un courant : j = q v δ(r - r'), où δ est la fonction de Dirac, la loi de Biot et Savart suggère d'écrire que cette charge (en mouvement) au point r' crée un champ magnétique au point r donné par
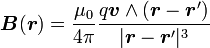 .
.
Attention, cette expression est en réalité une approximation, qui n'est valide que pour des vitesses vf très petites devant la vitesse de la lumière c. L'expression exacte du champ magnétique créé par une charge en mouvement est donnée par la formule de Liénard-Wiechert.
Application à l'aérodynamique
La loi de Biot et Savart est utilisée pour calculer la vitesse induite par des lignes de vortex en aérodynamique. En effet, une analogie avec la magnétostatique est possible si l'on admet que la vorticité correspond au courant, et la vitesse induite à l'intensité du champ magnétique.
Pour une ligne de vortex de longueur infinie, la vitesse induite est donnée par :
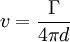 ,
,
où Γ est l'intensité du vortex et d la distance perpendiculaire entre le point et la ligne de vortex. Pour une ligne de vortex de longueur finie, on a
![v = \frac{\Gamma}{8 \pi d} \ \left[\cos A - \cos B \right]](/pictures/frwiki/98/b1d2d7cfa499cd407ed644537e8412ab.png) ,
,
où A et B sont les angles (orientés) entre la ligne et les deux extrémités du segment.
Bibliographie
- John David Jackson, Électrodynamique classique [« trad. de (en)Classical Electrodynamics »]
Voir aussi
- Portail de la physique
- Portail de l’électricité et de l’électronique
<<
Catégories : Loi en physique | Magnétostatique
Wikimedia Foundation. 2010.
