Parallelogramme

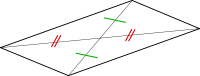
Un parallélogramme, en géométrie, est un quadrilatère (convexe) dont les côtés opposés sont parallèles deux à deux ; c'est un trapèze particulier.

Sommaire 1 Propriétés 2 Propriétés caractéristiques 3 Reconnaître un parallélogramme 3.1 Avec les diagonales 3.2 Avec les côtés 4 Aire d'un parallélogramme 5 Aspect abstrait 6 Un contre-exemple

Propriétés

Un parallélogramme a un centre de symétrie : le point d'intersection de ses diagonales.

Si un quadrilatère est un parallélogramme alors ses diagonales ont le même milieu.

Si un quadrilatère est un parallélogramme alors ses côtés opposés ont la même longueur.

Si un quadrilatère est un parallélogramme alors :

• ses angles opposés sont égaux ;
• ses angles consécutifs sont supplémentaires.

Propriétés caractéristiques

Les propriétés suivantes d'un quadrilatère sont équivalentes et définissent chacune un parallélogramme :

• des côtés opposés sont parallèles deux à deux,
• le quadrilatère est convexe et ses côtés opposés sont de même longueur deux à deux,
• ses diagonales se coupent en leur milieu,
• ABCD est un parallélogramme si ,
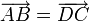• le quadrilatère est convexe et les angles opposés ont la même mesure deux à deux,
• les angles consécutifs sont supplémentaires deux à deux.

Reconnaître un parallélogramme

Avec les diagonales

Si les diagonales d'un quadrilatère ont le même milieu alors ce quadrilatère est un parallélogramme.

Avec les côtés

Si un quadrilatère (non croisé) a ses côtés opposés de même longueur alors ce quadrilatère est un parallélogramme.

Si un quadrilatère (non croisé) a une paire de côtés opposés parallèles et de même longueur alors ce quadrilatère est un parallélogramme.

Aire d'un parallélogramme

Soient la longueur d'un côté du parallélogramme et 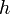la longueur de la hauteur associée. L'aire 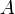du parallélogramme vaut :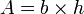

Aspect abstrait

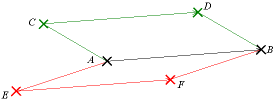
La notion de parallélogramme permet de définir la relation d'équipollence de deux bipoints, ce qui amène à la notion de vecteur en géométrie euclidienne :

• on appelle bipoint tout couple de points (l'ordre des points a une importance) ;
• deux bipoints (A,B) et (C,D) sont dits équipollents si ABDC est un parallélogramme, éventuellement aplati ;

on peut dire de manière équivalente que (A,B) et (C,D) sont équipollents si [AD] et [BC] ont le même milieu (ce qui règle le problème des parallélogrammes aplatis) ;

dans ce cas, les segments [AB] et [CD] sont parallèles et de même longueur, mais pas seulement : ils ont aussi « le même sens ».

La relation d'équipollence est une relation d'équivalence.

• on appelle vecteur 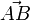la classe d'équivalence des bipoints équipollents à (A,B) ;

le vecteur 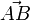est l'ensemble des bipoints satisfaisant la relation d'équipollence avec (A,B).

Un contre-exemple

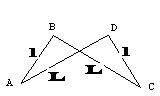
Contre exemple montrant l'importance de la convexité.

Un antiparallélogramme est un quadrilatère croisé dont les côtés opposés ont la même longueur deux à deux.

• Dans un antiparallélogramme, les angles opposés ont la même mesure.

• Portail de la géométrie