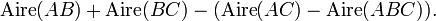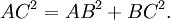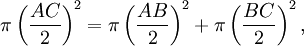- Theoreme des deux lunules
-
Théorème des deux lunules
Le théorème des deux lunules est un ancien théorème de géométrie plane.
Sommaire
Histoire
Ce théorème est très ancien : Hippocrate de Chios (-500) étudia aussi la duplication du cube, c’est-à-dire 21 / 3 (ne pas confondre avec Hippocrate(-460,-377)). On l'appelle aussi les lunules d'Hippocrate.
Définition
Une lunule est une portion de surface délimitée par deux cercles non concentriques de rayons différents, formant un croissant de lune en forme de ménisque : convexe d’un côté et concave de l’autre.
Énoncé
Soit le triangle ABC rectangle en B et
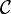le cercle circonscrit à ABC (de diamètre AC).La lunule LBC est la figure formée par le demi-disque de diamètre BC extérieur au triangle ABC, auquel on enlève son intersection avec le disque délimité par
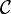.La lunule LBA est la figure formée par le demi-disque de diamètre BA extérieur au triangle ABC, auquel on enlève son intersection avec le disque délimité par
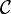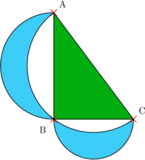
.Alors la somme des aires de LBC et de LBA (en bleu sur la figure) est égale à l'aire du triangle ABC (en vert).
Démonstration
Soit un triangle ABC rectangle en B
Les deux petites parties blanches sont le demi-cercle de diamètre AC privé du triangle ABC. Leur aire est donc Aire(AC) − Aire(ABC)
Les deux lunules sont les deux demi-cercles de diamètre AB et BC privés des parties blanches. Leur aire est donc
Pour montrer le théorème, il suffit donc de montrer que Aire(AB) + Aire(BC) − Aire(AC) = 0. C'est-à-dire que l'aire des deux demi-disques de diamètre AB et BC est égale à l'aire du demi-disque de diamètre AC.
Or le théorème de Pythagore nous dit que
Donc en multipliant par
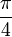on a quece qui est l'égalité des aires recherchées.
Voir aussi
Portail de la géométrie
Catégories : Géométrie du triangle | Cercle et sphère | Théorème de géométrie
Wikimedia Foundation. 2010.
