- Théorème de pythagore
-
Théorème de Pythagore
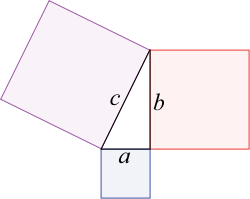
Le théorème de Pythagore est un théorème de géométrie euclidienne qui énonce que dans un triangle rectangle (qui possède un angle droit) le carré de la longueur de l’hypoténuse (côté opposé à l’angle droit) est égal à la somme des carrés des longueurs des deux autres côtés. Ce théorème est nommé d’après Pythagore de Samos, mathématicien, philosophe et astronome de la Grèce antique.
Sommaire
Énoncé du théorème
La forme la plus connue du théorème de Pythagore est la suivante :
Théorème de Pythagore — Dans un triangle rectangle, le carré de la longueur de l’hypoténuse (côté opposé à l’angle droit) est égal à la somme des carrés des longueurs des côtés de l’angle droit.
Note: Le terme « longueur », généralement oublié, est très important. En effet, la longueur est un nombre réel sur lequel l’opération d’élévation au carré est parfaitement définie ; l’hypoténuse est un segment de droite, objet géométrique pour lequel l’élévation au carré n’a pas de sens.
Cependant, il est parfois retiré afin de ne pas compliquer l'apprentissage du théorème (La notion de longueur étant sous-entendue)
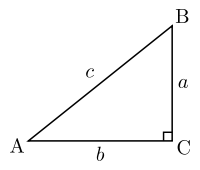
Dans un triangle ABC rectangle en C, AB étant l’hypoténuse, où AB = c, AC = b et BC = a (cf. figure ci-dessus), on aura donc : BC2 + AC2 = AB2 ou encore a2 + b2 = c2.
Le théorème de Pythagore permet ainsi de calculer la longueur d’un des côtés d’un triangle rectangle si on connaît les deux autres.
Exemple
Avec les notations ci-dessus, soit le triangle rectangle de côtés a = 3 et b = 4; alors la longueur du troisième côté, c, est donnée par : a2 + b2 = 32 + 42 = 25 = c2. Les longueurs étant des réels positifs, on obtient c = 5. Un triplet de nombres entiers tel que (3, 4, 5), représentant la longueur des côtés d’un triangle rectangle s’appelle un triplet pythagoricien.
Réciproque
La réciproque du théorème de Pythagore est également vraie :
Réciproque du théorème de Pythagore — Si dans un triangle, la somme des carrés de deux côtés est égale au carré du plus grand côté, alors ce triangle est rectangle.
Le théorème de Pythagore est donc une propriété caractéristique des triangles rectangles. Formulé autrement, si dans un triangle ABC on a BC2 + AC2 = AB2, alors ce triangle est rectangle en C.
Histoire
Que la propriété de Pythagore soit connue depuis l’Antiquité est un fait dont on peut trouver trace dans l’histoire. Il suffit pour cela d’observer la corde à treize nœuds dont se servaient les arpenteurs égyptiens. Cette corde permettait de mesurer des distances mais aussi de construire, sans équerre, un angle droit puisque les 13 nœuds (et les douze intervalles) permettaient de construire un triangle dont les dimensions étaient (3 - 4 - 5), triangle qui s’avère être rectangle. Cette corde restera un outil de géomètre pendant encore tout le Moyen Âge. La plus ancienne représentation de triplets pythagoriciens (triangle rectangle dont les côtés sont entiers) se trouve sur des mégalithes (au XXVe siècle av. J.-C., Grande-Bretagne). On retrouve aussi la trace de triplets pythagoriciens sur des tablettes babyloniennes (tablette de Plimpton 322 au XVIIIe siècle av. J.-C. qui prouvent que, plus de 1 000 ans avant Pythagore, les géomètres connaissaient l’existence de triplets pythagoriciens. Mais entre le constat : « on observe que certains triangles rectangles vérifient cette propriété », sa généralisation : « il semble que tous les triangles rectangles vérifient cette propriété » et sa démonstration : « il est vrai que tous les triangles rectangles dans un plan euclidien vérifient cette propriété », il faut souvent attendre plusieurs siècles.
Les preuves historiques de la vie de Pythagore sont déjà si rares qu’il n’est pas étonnant qu’on ne puisse pas lui attribuer avec certitude la paternité de la démonstration. La première trace écrite figure dans les Éléments d’Euclide (proposition XLVII) sous la forme suivante[1] :
« Aux triangles rectangles, le carré du côté qui soutient l'angle droit, est égal aux carrés des deux autres côtés. »
Sa réciproque est la proposition XLVIII[1] :
« Si le carré de l’un des côtés d’un triangle est égal aux carrés des deux autres côtés, l’angle soutenu par ces côtés est droit. »
Cependant, les commentaires de Proclos des Éléments d’Euclide (Autour de 400) semblent indiquer qu’Euclide n’aurait fait que retranscrire une démonstration plus ancienne que Proclos attribue à Pythagore. C’est donc entre le VIe siècle av. J.-C. et le IIIe siècle av. J.-C. que l’on peut dater la démonstration de cette propriété. On raconte que c’est à cette occasion qu’aurait été découverte l’existence de nombres irrationnels. En effet, il est facile de construire un triangle rectangle isocèle de côté 1. Alors le carré de l’hypoténuse vaudrait 2. Or une démonstration simple accessible du temps de Pythagore prouve qu’aucun rationnel n’a un carré égal à 2. On raconte que cette découverte fut tenue secrète par l’école pythagoricienne sous peine de mort.
Parallèlement à ces découvertes, il semble qu’en Chine aussi la propriété soit connue. On retrouve trace de l’existence de ce théorème dans un des plus anciens ouvrages mathématiques chinois le Zhoubi suanjing. Cet ouvrage, écrit probablement durant la dynastie Han (-206 à 220), regroupe des techniques de calcul datant de la dynastie Zhou (Xe siècle av. J.-C. à -256). Une démonstration du théorème, qui porte en Chine le nom de théorème de Gougu (base et altitude), figure dans le Jiuzhang suanshu (Les neuf chapitres sur l'art mathématique, -100 à 50), démonstration qui ne ressemble en rien à celle d’Euclide et qui prouve l’originalité de la démarche chinoise.
En Inde, vers -300, on trouve la trace d’une démonstration numérique de la propriété (preuve effectuée sur des nombres particuliers mais qui peut se généraliser aisément). D’une propriété géométrique, le théorème de Pythagore prend aussi un développement arithmétique avec la recherche de tous les triplets d’entiers associés aux trois côtés d’un triangle rectangle : ce sont les triplets pythagoriciens. Cette recherche ouvrira la porte à une autre : la recherche de triplets vérifiant l’égalité an + bn = cn, recherche qui conduit à la conjecture de Fermat résolue en 1994 par Andrew Wiles. Il existe en réalité de nombreuses démonstrations de ce théorème, de celle d’Euclide à celle des Chinois, en passant par celle de l’Inde, celle utilisant des similitudes, celle de Léonard de Vinci et même celle du président américain James Garfield. On ne peut pas passer sous silence Al Kashi qui donne pour un triangle quelconque une relation dont la formule de Pythagore devient alors le cas particulier du triangle rectangle : le Théorème d'Al-Kashi.
Démonstrations
C’est sans doute le théorème qui possède le plus grand nombre de preuves connues (la loi de réciprocité quadratique se distingue aussi dans ce domaine). Une des plus anciennes dont on a gardé trace est celle d’Euclide qui utilise la propriété du cisaillement, mais il existe aussi d’autres preuves, uniquement visuelles fondées sur des puzzles, c’est le cas de la justification chinoise du théorème de Gougu. Des preuves modernes mettant en jeu des propriétés algébriques ont été développées ultérieurement. Une autre utilisant des similitudes est parfois attribuée à Pythagore. Il existe de nombreuses autres démonstrations du théorème de Pythagore ; le vingtième président des États-Unis, James Abram Garfield en développa une lui-même, très voisine de la preuve moderne. L’une des plus intéressantes est la preuve calculatoire basée sur la formule d'Euler.
La preuve selon Euclide
La démonstration du théorème utilise deux propositions, déjà démontrées dans les Éléments. La première est la proposition XXXV du 1er livre[1] :
« Les parallélogrammes constitués sur une même base, et entre mêmes parallèles, sont égaux entre eux. »
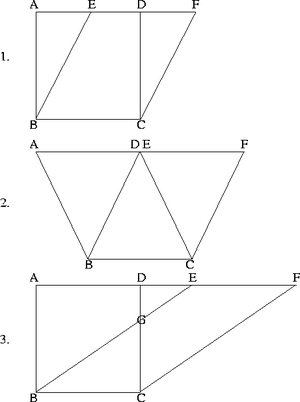
Considérons les deux parallélogrammes ABCD et BCFE, les deux sur la même base, BC, et entre les mêmes parallèles, BC et AF. On a AD qui est égal à BC (car ce sont les deux bases du parallélogramme ABCD), et BC qui est égal à EF (car ce sont les deux bases du parallélogramme BCFE), alors AD est égal à EF. Or, il n’y a que trois possibilités (montrées dans l’image) pour la position du point E relatif à D ; E peut être à la gauche de D, au point D, ou à la droite de D. Examinons chaque cas:
- Si E tombe à la gauche de D, ED est la partie commune de AD et EF, alors il est possible de vérifier que AD et EF sont égaux. Mais notez que les côtés AB et DC sont égaux, car ils sont des côtés opposés du parallélogramme ABCD. Aussi, parce que les points A, E, D et F sont colinéaires, les angles BAE et CDF sont égaux. Par conséquent, les triangles BAE et CDF sont égaux, parce que deux côtés de l’un sont égaux à deux côtés de l’autre, et un angle est commun. Donc les parallélogrammes ABCD et CBEF ne sont que des différents rangements du trapèze BEDC et le triangle BAE (ou CDF). CQFD
- Si E tombe au point D, on trouve d’une façon semblable à 1 que les triangles BAE et CDF sont égaux, et alors qu’il est possible d’obtenir les parallélogrammes ABCD et BCFE en ajoutant à la partie commune BCD le triangle BAE (ou bien CDF). CQFD
- Si E tombe à la droite de D, notez que, parce que les segments AD et EF sont égaux, en ajoutant à chacun la ligne DE, nous trouvons que AE et DF sont égaux. Par un argument semblable à ceux utilisés dans les cas 1 et 2, il est possible de prouver que les triangles BAE et CDF, et par conséquent les trapèzes BADG et CGEF, sont égaux. Alors, il est évident que les parallélogrammes ABCD et CBEF sont obtenus en ajoutant au triangle commun BCG le trapèze BADG (ou CGEF). CQFD
Le remplacement d’un parallélogramme par un autre de même base et même hauteur, justifié par cette proposition, est connu en mathématiques sous le nom de cisaillement. Le cisaillement sera très important dans la preuve de la proposition XLI[1] :
« Si un parallélogramme, et un triangle ont une même base, et sont entre mêmes parallèles ; le parallélogramme sera double du triangle. »
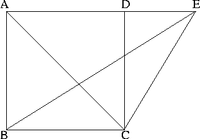
Considérons un parallélogramme ABCD, et soit E un point sur l’extension de AD. Nous voulons démontrer que l’aire de ABCD est deux fois l’aire de BEC. Traçant la diagonale AC, nous voyons que l’aire de ABCD est deux fois l’aire de ABC. Mais, l’aire du triangle ABC est égale à l’aire du triangle BEC, car ils ont la même base. Alors, deux fois l’aire de BEC égale deux fois l’aire de ABC, c’est-à-dire l’aire de ABCD. Nous avons montré que ABCD (qui est double de ABC) est double de BEC. CQFD
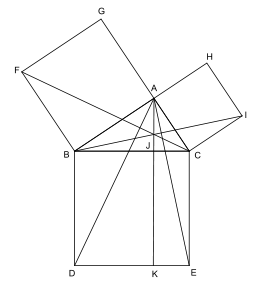
Maintenant, nous pouvons passer à la démonstration du théorème en tant que telle. Considérons le triangle ABC rectangle en A. Soient BCED, ABFG et ACIH les carrés des côtés BC, AB et AC respectivement. Soit J l’intersection de AK et de BC. Ce que nous voulons démontrer est que l’aire de BCED est égale à de la somme des aires de ABFG et ACIH. Nous prouvons ce fait en démontrant que l’aire du carré ABFG est égale à l’aire du rectangle BJKD et que l’aire du carré ACIH est égale à l’aire du rectangle CEKJ. Démontrons la première égalité, notons que les côtés FB et BC sont égaux aux côtés AB et BD, respectivement. Parce que les angles ABF et CBD sont égaux, les angles FBC (FBA + ABC) et ABD (ABC + CBD) sont égaux. Par conséquent, les triangles FBC et ABD sont égaux aussi. Or, notez que, par la proposition XLI, l’aire du carré ABFG est double de celle du triangle FBC et que l’aire du rectangle BJKD est double de celle du triangle ABD. Comme FBC et ABD sont égaux, l’aire de ABFG est bien égale à celle de BJKD. La seconde égalité se prouve d’une manière semblable : observant que IC et CB égalent AC et CE, respectivement, et que l’angle ICB égale l’angle ACE, nous concluons que les triangles ICB et ACE sont égaux. Puis, sachant que l’aire du carré ACIH est double de celle de ICB et que l’aire du rectangle CEKJ est double de celle de ACE, et que le triangle ICB est égal au triangle ACE, l’aire de ACIH est donc égale à l’aire de CEKJ. En conséquence, l’aire de BCED, égale à la somme de l’aire de BJKD et de celle de CEKJ, est bien égale à la somme de l’aire de ABFG et de celle de ACIH. CQFD. Cette démonstration peut se généraliser pour les autres triangles (théorème de Clairaut). Cette propriété peut aussi s'appliquer à d'autres figures que des carrés (paragraphe suivant)
Généralisation à d’autres figures que des carrés
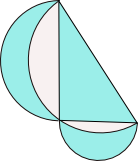 Propriété des lunules
Propriété des lunules
Une autre généralisation de la démonstration du théorème de Pythagore fut déjà énoncée par Euclide dans ses Éléments (Proposition 31 du livre VI[1]) :
« Dans les triangles rectangles, la figure construite sur le côté qui sous-tend l’angle droit, est égale aux figures semblables et semblablement décrites sur les côtés qui comprennent l’angle droit. »
Autrement dit :
« Si on érige des figures semblables sur les côtés d’un triangle droit, alors la somme des aires des deux plus petites figures égale l’aire de la plus grande. »
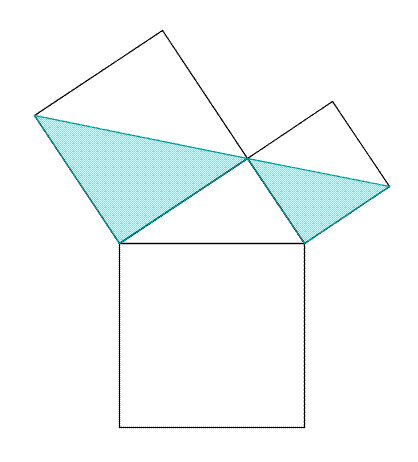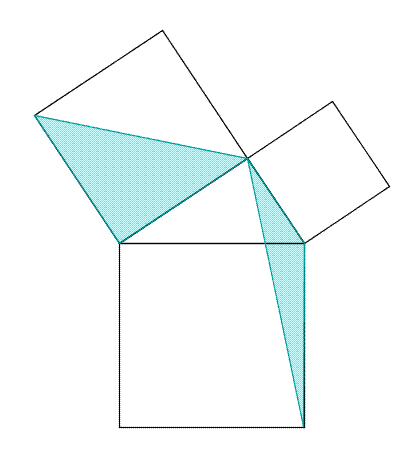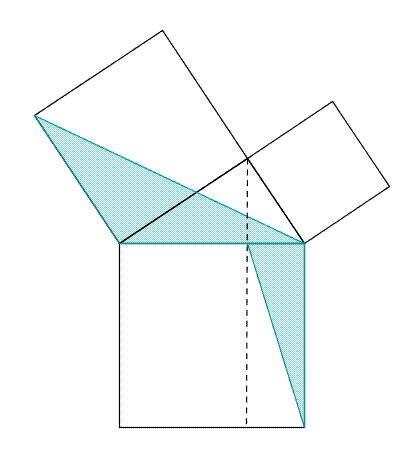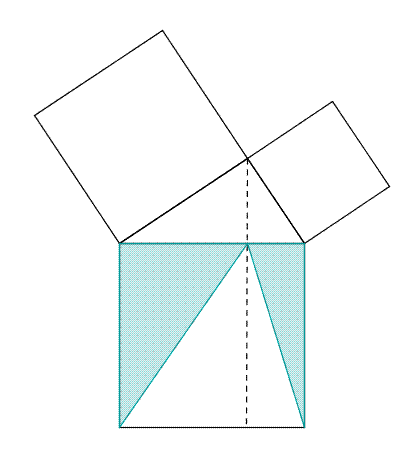
Cette propriété permet de montrer que l’aire du triangle rectangle est égale à la somme des aires des lunules dessinées sur chaque côté de l’angle droit (théorème des deux lunules). Cette idée a été utilisée par Henri Lebesgue pour fournir une démonstration simplissime du théorème. Il choisit, comme figures semblables, le triangle rectangle de départ en remarquant que la hauteur relative à l’hypoténuse décompose le triangle initial en deux triangles semblables. Cette démonstration peut être comparée avec la démonstration avec des similitudes ci-dessous.
Une preuve du théorème de Gougu (Chine)
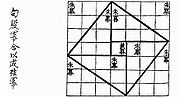
Le théorème de Gougu[2] est reconstitué d’après les commentaires du mathématicien chinois Liu Hui (IIIe siècle apr. J.-C.) sur le JiuZhang SuanShu 九章算術 « neuf chapitres d'Arithmétique » (206 av.–220 apr. J.-C.), et le Zhoubi Suanjian 周髀算經, « l’ombre des cycles, livre de calculs » (un livre d’astronomie). Le neuvième chapitre du livre Les neuf chapitres, classique mathématique de la chine ancienne, s’ouvre sur un énoncé du théorème de Pythagore avec le commentaire laconique : : « la base multipliée par elle-même fait un carré vermillon, la hauteur multipliée par elle même un carré bleu-vert et l’on fait en sorte que ce qui entre et ce qui sort se compense l’un l’autre ». Cette preuve utilise le principe du puzzle : deux surfaces égales après découpage fini et recomposition ont même aire. Euclide, dans sa propriété de cisaillement, utilise le même principe.
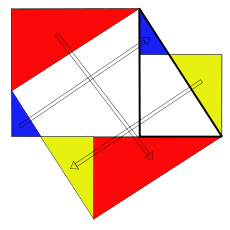
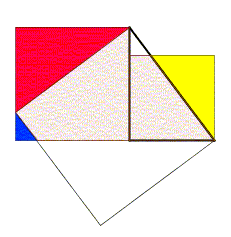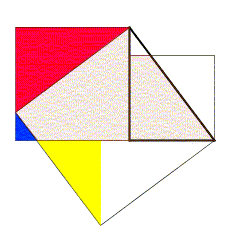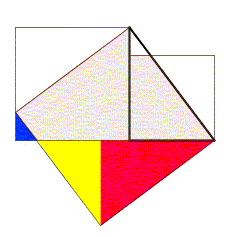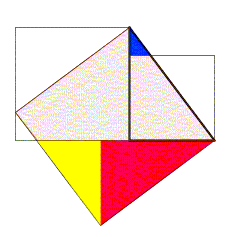
Dans la figure ci-dessus, le triangle rectangle est tracé en gras, le carré de la hauteur a été tracé à l’extérieur du triangle, le carré de la base et celui de l’hypoténuse sont tournés vers le triangle. Les parties des carrés des côtés de l’angle droit qui dépassent du carré de l’hypoténuse ont été découpées et replacées à l’intérieur de ce carré. Le triangle rouge est égal au triangle de départ. Le triangle jaune a pour grand côté de l’angle droit le petit côté du triangle de départ et a mêmes angles que le triangle initial. Le triangle bleu a pour grand côté de l’angle droit, la différence des côtés du triangle initial et a mêmes angles que le triangle initial.L’apparition d’une illustration pour cette procédure est très tardive. Selon Karine Chemla, l’absence d’illustration serait due au fait que la figure de référence était déjà connue et correspondrait à la propriété liant le carré de l’hypoténuse avec le carré de la différence des côtés et l’aire du triangle initial[3] : c2 = (a − b)2 + 2ab.
Une preuve moderne
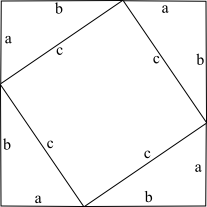
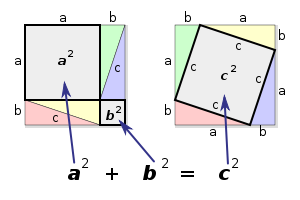
Considérons un triangle rectangle dont les côtés sont de longueurs a, b et c. Ensuite recopions ce triangle trois fois et plaçons le triangle et ses copies de manière à avoir le côté a de chacun aligné au côté b d’un autre, et pour que les jambes des triangles forment un carré dont le côté est a + b, comme dans l’image. Puis, nous essayons de trouver l’aire du carré formé par les côtés c. Évidemment, c’est c2, mais c’est aussi égal à la différence entre l’aire du carré extérieur et la somme des aires des triangles. L’aire du carré est (a + b)2 (car son côté est a + b) et l’aire totale des triangles est quatre fois l’aire d’un seul, c’est-à-dire 4(ab / 2), donc la différence est (a + b)2 − 4(ab / 2), ce qu’on peut simplifier comme a2 + 2ab + b2 − 2ab, ou bien a2 + b2. Nous avons démontré que l’aire du carré de côté c est égale à a2 + b2 ; en effet, c2 = a2 + b2. CQFDRemarque : il faut démontrer que le carré de côté "c" en est bien un. C'est un losange car c'est un quadrilatère ayant 4 côtés de même longueur,. De plus, il possède des angles droits : en effet, la somme d'un angle du quadrilatère et des deux angles qui lui sont adjacents donne un angle plat; alors que la somme de ces deux angles du triangle rectangle donne un angle droit. La figure centrale et donc bien un carré.
Démonstration avec des similitudes
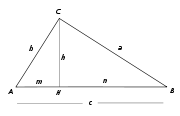
Il n’y a pas trace de la démonstration qu’aurait conçue Pythagore et les historiens envisagent deux types de démonstrations : ou bien une démonstration fondée sur un découpage comme celui de Gougu ou une démonstration utilisant les proportionnalités des triangles découpés par la hauteur issue de l’angle droit[4].
Si H est le pied de la hauteur issue de C, les triangles CAB, HAC et HCB sont semblables (par égalités des angles). Le rapport de similitude entre les triangles HAC et CAB est le rapport des hypoténuses AC/AB, de même le rapport de la similitude entre les triangles HCB et CAB est CB/AB. Le rapport des aires est alors égal au carré du rapport de la similitude, soit :
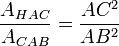 et
et 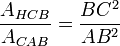 .
.Comme d’autre part la somme des aires des triangles HAC et HCB donne l’aire du triangle CAB, on peut écrire :
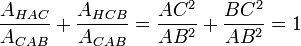 . Soit encore : AC2 + BC2 = AB2.CQFD
. Soit encore : AC2 + BC2 = AB2.CQFDOn peut également proposer une variante plus élémentaire de cette démonstration afin de s’affranchir de la notion d’aire : Le rapport de similitude entre les triangles HAC et CAB implique
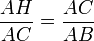 soit
soit 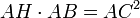 . De même, le rapport de similitude entre les triangles HCB et CAB implique
. De même, le rapport de similitude entre les triangles HCB et CAB implique 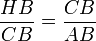 soit
soit 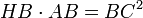 en additionnant, il vient
en additionnant, il vient 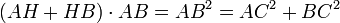 . CQFD
. CQFDCette démonstration est à rapprocher de celle du théorème de Ptolémée en prenant un rectangle comme quadrilatère.
Variations sur le théorème
Contraposée
La contraposée du théorème affirme ceci :
Théorème — Si les longueurs des côtés d’un triangle ABC vérifient
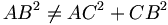 , alors le triangle n’est pas rectangle en C.
, alors le triangle n’est pas rectangle en C.La contraposée est logiquement équivalente au théorème direct, elle n’a en revanche pas le même usage en démonstration puisque le théorème sert à calculer le troisième côté manquant d’un triangle rectangle, alors que la contraposée sert à démontrer qu’un triangle dont on connaît les longueurs des trois côtés n’est pas rectangle.
Contraposée de la réciproque
Enfin, la contraposée de la réciproque du théorème de Pythagore stipule ceci :
Théorème — Si le triangle ABC n’est pas rectangle en C alors
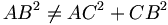 .
.Généralisation à des triangles quelconques
Le théorème d'Al-Kashi est une généralisation du théorème de Pythagore à des triangles quelconques.
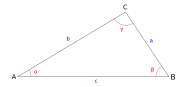
Soit un triangle ABC, dans lequel on utilise les notations usuelles exposées sur la figure c-dessus : d’une part α, β et γ pour les angles et, d’autre part, a, b et c pour les côtés respectivement opposés à ces angles. Alors, le théorème d’al-Kashi s’énonce de la façon suivante :
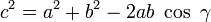 .
.Utilisations
- En coordonnées cartésiennes dans un repère orthonormé, le théorème de Pythagore permet d’exprimer la distance entre deux points du plan : ainsi, si A(xa,ya) et B(xb,yb) sont des points du plan euclidien, la distance les séparant est donnée par : :
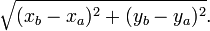 : En effet, si C est le point de coordonnées (xb,ya), le triangle ACB est rectangle en C, les distances CA et CB sont données par CA= |xb - xa| et CB = |yb - ya| et la distance AB représente l’hypoténuse du triangle rectangle ACB.
: En effet, si C est le point de coordonnées (xb,ya), le triangle ACB est rectangle en C, les distances CA et CB sont données par CA= |xb - xa| et CB = |yb - ya| et la distance AB représente l’hypoténuse du triangle rectangle ACB. - Plus généralement, dans un espace euclidien (ou dans un espace affine euclidien) de dimension finie, la distance de
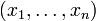 à
à 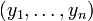 s’écrit :
s’écrit :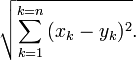
- L’identité de Parseval peut être vue comme une généralisation du théorème de Pythagore aux familles infinies de vecteurs d'un espace préhilbertien.
- Le théorème de Pythagore se généralise aussi dans les simplexes de plus haute dimension. Si un tétraèdre possède un coin formé d’angle droit (un coin de cube), alors le carré de l’aire de la face opposée au coin est la somme des carrés des aires des trois autres faces. Ce théorème est aussi connu sous le nom de théorème de Gua.
Théorème de Pythagore dans d’autres espaces
Écriture vectorielle
En faisant intervenir le concept de vecteur, on peut reformuler le théorème comme suit :
« Étant donnés deux vecteurs
 et
et  ,
, 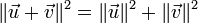 si et seulement si
si et seulement si 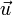 et
et 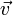 sont orthogonaux. »
sont orthogonaux. »De manière générale, on a simplement l’inégalité triangulaire : :
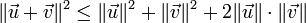 que l’on écrit en général :
que l’on écrit en général :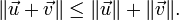
Dans un espace préhilbertien
Le théorème de Pythagore découle en fait directement de la définition du produit scalaire, et se généralise à tout espace préhilbertien. Dans ce cadre général, il affirme que si u et v sont deux vecteurs orthogonaux, alors : :
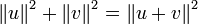 . La réciproque est vraie dans le cas réel. De plus, cette formule se généralise à une famille de vecteurs orthogonaux. Pour elle, la somme des carrées des normes est égale au carré de la norme de la somme. Ce résultat très général permet notamment de démontrer l’inégalité de Bessel, et l’égalité de Parseval.
. La réciproque est vraie dans le cas réel. De plus, cette formule se généralise à une famille de vecteurs orthogonaux. Pour elle, la somme des carrées des normes est égale au carré de la norme de la somme. Ce résultat très général permet notamment de démontrer l’inégalité de Bessel, et l’égalité de Parseval.En géométrie non euclidienne
Cette propriété résiste mal au transfert dans d’autres géométries à cause de leur courbure :
- si la courbure est positive (géométrie sphérique), on obtient : c2 < a2 + b2 ;
- si la courbure est négative (géométrie hyperbolique), on obtient : c2 > a2 + b2 ;
- en particulier, pour tout triangle rectangle en géométrie hyperbolique, avec une courbure de -1, le théorème de Pythagore prend la forme suivante :
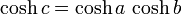 où cosh est le cosinus hyperbolique. En utilisant le développement limité d’ordre 2 de cette fonction, on retrouve bien, pour de petites valeurs des côtés, la forme classique du théorème de Pythagore.
où cosh est le cosinus hyperbolique. En utilisant le développement limité d’ordre 2 de cette fonction, on retrouve bien, pour de petites valeurs des côtés, la forme classique du théorème de Pythagore.
- en particulier, pour tout triangle rectangle en géométrie hyperbolique, avec une courbure de -1, le théorème de Pythagore prend la forme suivante :
- si la courbure est nulle (géométrie plane ou cylindrique), on conserve : c2 = a2 + b2.
Plus précisément, pour tout triangle rectangle sur une sphère de rayon R, le théorème de Pythagore prend la forme suivante :
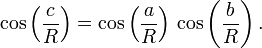
En utilisant un développement limité d’ordre 2 de la fonction cosinus, on retrouve bien, pour des grandes valeurs de R, la formule classique du théorème de Pythagore.
Espace physique
Comme le théorème de Pythagore est dérivé d’axiomes de la géométrie euclidienne, et que les espaces physiques ne sont pas toujours euclidiens, il ne doit pas être valide pour les triangles dans les espaces physiques. L’un des premiers mathématiciens à réaliser ceci fut Carl Friedrich Gauss, qui mesura donc attentivement de grands triangles rectangles dans le cadre de son étude géographique afin de vérifier ce théorème. Il ne trouva aucun contre-exemple avec sa précision de mesure. La théorie de la relativité générale soutient que la matière et l’énergie conduisent l’espace à être non-euclidien et le théorème ne s’applique donc pas strictement en présence d’énergie. Cependant, la déviation par rapport à l’espace euclidien est faible sauf auprès d’imposantes sources gravitationnelles comme les trous noirs. Déterminer si le théorème est enfreint sur d’importantes échelles cosmologiques, c’est-à-dire mesurer la courbure de l’Univers, est un problème ouvert pour la cosmologie.
Notes et références
- ↑ a , b , c , d et e Éléments d'Euclide
- article Wikipédia
- Référence
- [pdf] en ligne sur le sute de la BNF (Ressources Gallica) Livre I : proposition XXXV p. 62, proposition XLI p. 69, proposition XLVII p. 76, proposition XLVIII p. 78; Livre VI : proposition XXXI p. 241
- ↑ Voir par exemple (en) Proof of Guogu or Pythagoras' Theorem ou bien Quelques exemples de démonstration en mathématiques chinoises, Jean-Claude Martzloff, in La démonstration mathématique dans l’histoire, Irem de Lyon
- ↑ Karine Chemla, Guo Shuchun, Neuf Chapitres. Le Classique de la Chine ancienne et ses commentaires. Edition critique" [détail des éditions], p 680
- ↑ Eliane Cousquer, Le Théorème de Pythagore[pdf]
Annexes
Articles connexes
- Algèbre linéaire
- Courbure spatiale
- Dernier théorème de Fermat
- Livre I des Éléments d'Euclide
- Théorème de Clairaut (géométrie), un cas plus général, avec des parallélogrammes autour d'un triangle quelconque
- Théorème d'Al-Kashi (Le Théorème de Pythagore généralisé) avec un peu de trigonométrie
- Triplet pythagoricien
Liens externes
 Wikibooks possède des exercices sur le théorème de Pythagore.
Wikibooks possède des exercices sur le théorème de Pythagore.- [pdf] Le théorème de Pythagore par Éliane Cousquer
- (fr) Animation de Pythagore, une animation de la démonstration d'Euclide sur le site kangmath
- (en) Proposition de 78 démonstrations différentes par Alexander Bogomolny
- (fr) Application online pour faire des calculs avec le théorème de Pythagore et sa réciproque avec gestion des unités, des arrondis et avec toutes les étapes intermédiaires pour bien comprendre, par Benoît Grunenberger
- Portail de la géométrie
Catégories : Article de qualité | Théorème de géométrie | Géométrie du triangle | Histoire des mathématiques | Mathématiques élémentaires
Wikimedia Foundation. 2010.