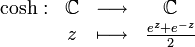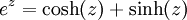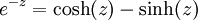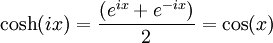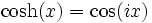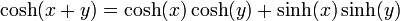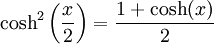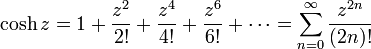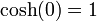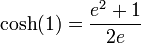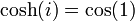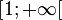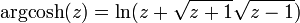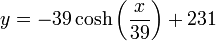Cosinus Hyperbolique

Cosinus hyperbolique

Graphe de la fonction cosinus hyperbolique sur une partie de $\mathbb R$

Le cosinus hyperbolique est, en mathématiques, une fonction hyperbolique.

Sommaire

1 Définition
2 Propriétés
3 Valeurs
4 Zéros
5 Fonction réciproque
6 Utilisation
- 6.1 Physique
- 6.2 Architecture
7 Voir aussi

Définition

La fonction cosinus hyperbolique, notée cosh (parfois, mais plus rarement, ch) est la fonction complexe suivante :

$\begin{matrix} \cosh: &\mathbb C &\longrightarrow &\mathbb C \\ \ &z &\longmapsto &\frac {e^z+e^{-z}} {2} \end{matrix}$

où $e$ est la fonction exponentielle complexe.

La fonction cosinus hyperbolique est en quelque sorte l'analogue de la fonction cosinus dans la géométrie hyperbolique.

Propriétés

Propriétés générales

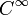
cosh est continue et infiniment dérivable, dite de classe $C^\infty$
La dérivée de cosh est sinh, la fonction sinus hyperbolique.
La primitive de cosh est sinh+C, à une constante d'intégration C près.
La restriction de cosh à $\mathbb R$ est paire et strictement croissante sur 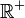$\mathbb R^+$ .

Propriétés trigonométriques

De par les définitions des fonction cosinus et sinus hyperbolique, on peut déduire les égalités suivantes :

$e^z = \cosh(z) + \sinh(z) \,$

$e^{-z} = \cosh(z) - \sinh(z) \,$

Ces égalités sont analogues à la formule d'Euler en trigonométrie classique.

De même que les coordonnées (cos(t), sin(t)) définissent un cercle, (cosh(t),sinh(t)) définissent la branche positive d'une hyperbole équilatérale. On a en effet pour t>0 :

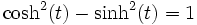$\cosh^2(t) - \sinh^2(t) = 1 \,$ .

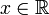D'autre part, pour $x \in \mathbb R$ :

$\cosh(i x) = \frac{(e^{i x} + e^{-i x})}{2} = \cos(x)$

$\cosh(x) = \cos(i x) \,$

$\cosh(x+y) = \cosh(x) \cosh(y) + \sinh(x) \sinh(y) \,$

$\cosh^2\left(\frac{x}{2}\right) = \frac{1+\cosh(x)}{2}$

Développement en série de Taylor

cosh, étant indéfiniment dérivable, possède un développement en série de Taylor en tout point :

$\cosh z = 1 + \frac {z^2} {2!} + \frac {z^4} {4!} + \frac {z^6} {6!} + \cdots = \sum_{n=0}^\infty \frac{z^{2n}}{(2n)!}$

Valeurs

Quelques valeurs de cosh :

$\cosh(0) = 1 \,$
$\cosh(1) = \frac {e^2+1}{2e}$
$\cosh(i) = \cos(1) \,$

Zéros

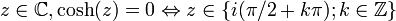Tous les zéros de $cosh$ sont des imaginaires pures : $z\in \mathbb{C}, \cosh(z)=0 \Leftrightarrow z \in \{i( \pi / 2 + k \pi ) ; k \in \mathbb{Z}\}$ .

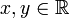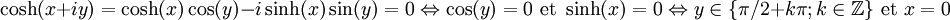Démonstration: Soit $z = x + i y$ avec $x,y \in \mathbb{R}$ . On a alors : $\cosh(x+i y)=\cosh(x)\cos(y)-i\sinh(x)\sin(y)=0 \Leftrightarrow \cos(y)=0 \mbox{ et } \sinh(x)=0 \Leftrightarrow y \in \{\pi / 2 +k \pi ; k \in \mathbb{Z}\} \mbox{ et } x=0$ .

Fonction réciproque

Graphe de la fonction argument cosinus hyperbolique sur $\left[1;+\infty\right[$

cosh admet une fonction réciproque, notée argcosh (ou argch), et nommée argument cosinus hyperbolique. Il s'agit d'une fonction à valeurs multiples complexe. Sa branche principale est généralement choisie en posant comme coupure le segment $\left]-\infty;1\right[$ .

$\operatorname{argcosh}(z) = \ln(z + \sqrt{z+1} \sqrt {z-1})$

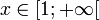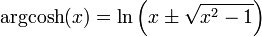Pour $x \in \left[1;+\infty\right[$ , la restriction de cosh à $\mathbb R$ admet deux réciproques : $\operatorname{argcosh}(x)=\ln\left(x \pm \sqrt{x^2-1}\right)$ .

Utilisation

Physique

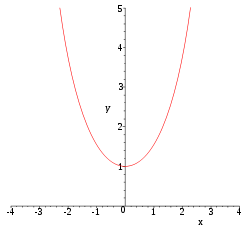
La courbe représentative de la fonction cosh sur $\mathbb R$ décrit une chaînette, c’est-à-dire la forme d'un câble fixé aux deux extrémités et soumis à la pesanteur.

Architecture

L'arche du Gateway

L'arche du Gateway à Saint-Louis (Missouri) possède la forme d'une chaînette renversée. Elle s'élève à 192 m en son centre et enjambe 192 m à sa base. Les points de cette arche satisfont approximativement l'équation

$y=-39 \cosh \left( \frac{x}{39} \right)+231$

pour -96 < x < 96.

Voir aussi

Portail des mathématiques

Ce document provient de « Cosinus hyperbolique ».

Catégories : Géométrie hyperbolique | Trigonométrie

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Cosinus Hyperbolique de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

Cosinus hyperbolique — Graphe de la fonction cosinus hyperbolique sur une partie de Le cosinus hyperbolique est, en mathématiques, une fonction hyperbolique. Sommaire … Wikipédia en Français
Cosinus Hyperbolique Réciproque — Le cosinus hyperbolique réciproque est, en mathématiques, une fonction hyperbolique. Définition La fonction cosinus hyperbolique réciproque, notée Argch (ou arccosh) est la fonction suivante : Voir aussi Fonction hyperbolique Ce document… … Wikipédia en Français
Cosinus hyperbolique reciproque — Cosinus hyperbolique réciproque Le cosinus hyperbolique réciproque est, en mathématiques, une fonction hyperbolique. Définition La fonction cosinus hyperbolique réciproque, notée Argch (ou arccosh) est la fonction suivante : Voir aussi… … Wikipédia en Français
Cosinus hyperbolique d'un réel x — ● Cosinus hyperbolique d un réel x réel noté ch x égal à … Encyclopédie Universelle
Cosinus hyperbolique réciproque — Le cosinus hyperbolique réciproque est, en mathématiques, une fonction hyperbolique. Définition La fonction cosinus hyperbolique réciproque, notée Argch (ou arccosh) est la fonction suivante … Wikipédia en Français
Fonction cosinus hyperbolique — ● Fonction cosinus hyperbolique fonction définie sur R : x ↦ ch x … Encyclopédie Universelle
cosinus — [ kɔsinys ] n. m. • co sinus 1717; de co et sinus ♦ Fonction trigonométrique faisant correspondre à l angle de deux axes la mesure de la projection orthogonale sur l un, d un vecteur unitaire porté par l autre; sinus de l angle complémentaire.… … Encyclopédie Universelle
hyperbolique — [ ipɛrbɔlik ] adj. • 1541; lat. hyperbolicus, gr. huperbolikos I ♦ Rhét. Caractérisé par l hyperbole. Style hyperbolique. Cour. Des compliments hyperboliques. ⇒ emphatique, grandiloquent. Philos. Le doute hyperbolique (Descartes). II ♦ (1646) 1 ♦ … Encyclopédie Universelle
Cosinus (Homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom … Wikipédia en Français
Hyperbolique — Fonction hyperbolique En mathématiques, on appelle fonctions hyperboliques les fonctions cosinus hyperbolique, sinus hyperbolique et tangente hyperbolique. Les noms de sinus, cosinus et tangente proviennent de leur ressemblance avec les fonctions … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Cosinus Hyperbolique