Theoreme de Ptolemee

Theoreme de Ptolemee: Théorème de Ptolémée

Figure du théorème de Ptolémée.

Le théorème de Ptolémée est un théorème de géométrie euclidienne portant sur les diagonales d'un quadrilatère. L'implication directe est attribuée à l'astronome et mathématicien grec Ptolémée, dont il se servit pour ses calculs liés à l'astronomie.

Sommaire

1 Énoncé

2 Démonstration de l'implication directe

2.1 Par raisonnement géométrique

3 Démonstration de la réciproque

4 Lemme

5 Voir aussi

6 Liens externes

Énoncé

Théorème de Ptolémée — Un quadrilatère convexe est inscriptible si et seulement si le produit des longueurs des diagonales est égal à la somme des produits des longueurs des côtés opposés.

Avec les notations de la figure, ce théorème peut être traduit par :

Théorème de Ptolémée — Soit un quadrilatère convexe $A B C D$ ,
$A B C D$ est inscriptible 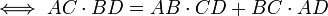$\iff AC \cdot BD = AB \cdot CD + BC \cdot AD\,$

Démonstration de l'implication directe

Par raisonnement géométrique

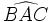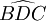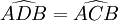Soit $A B C D$ un quadrilatère inscriptible non croisé. Les angles $\widehat{BAC}$ et $\widehat{BDC}$ sont égaux, car ils interceptent le même arc (voir théorème de l'angle inscrit) ; de même $\widehat{ADB} = \widehat{ACB}$ .

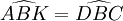Construisons le point K tel que $K \in [AC]$ et $\widehat{ABK} = \widehat{DBC}$ .

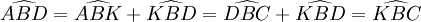On a alors $\widehat{ABD} = \widehat{ABK}+\widehat{KBD} = \widehat{DBC}+\widehat{KBD} = \widehat{KBC}$ .

Ainsi, les triangles $A B K$ et $D B C$ sont semblables (figure du milieu), de même que $A B D$ et $K B C$ (figure de droite).

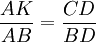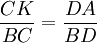
On obtient les relations suivantes (voir triangle semblable) : $\frac{AK}{AB} = \frac{CD}{BD}$ et $\frac{CK}{BC} = \frac{DA}{BD}$

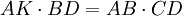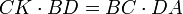
d'où $AK \cdot BD = AB \cdot CD$ et $CK \cdot BD = BC \cdot DA$

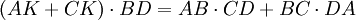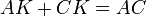en additionnant il vient $(AK+CK) \cdot BD = AB \cdot CD + BC \cdot DA$ et par construction $AK+CK = AC\,$ .

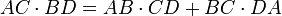On en déduit l'égalité du théorème : $AC \cdot BD = AB \cdot CD + BC \cdot DA$ .

Démonstration de la réciproque

(1) Nous admettrons que l'antécédent d'une droite $d$ par l'inversion de pôle A et de rapport k non nul telle que A n'appartient pas à $d$ est un cercle passant par A, privé de A.

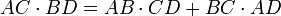
Soient A,B,C et D quatre points distincts tels que $AC \cdot BD = AB \cdot CD + BC \cdot AD\,$

Considérons l'inversion de pôle A et de rapport 1, qui transforme B en B', C en C' et D en D'.

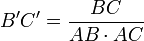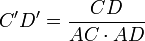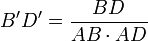Il vient : $B'C' = \frac{BC}{AB \cdot AC}$ , de même $C'D' = \frac{CD}{AC \cdot AD}$ et $B'D' = \frac{BD}{AB \cdot AD}$ .

En divisant notre première égalité par 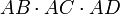$AB \cdot AC \cdot AD\,$ , on obtient :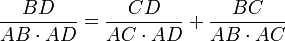 $\frac{BD}{AB \cdot AD} = \frac{CD}{AC \cdot AD} + \frac{BC}{AB \cdot AC}$

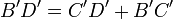
Soit encore : $B'D' = C'D' + B'C'\,$

Ainsi les points B', C' et D' sont alignés. D'après (1) : B, C et D appartiennent à un cercle passant par A. Le quadrilatère $A B C D$ est donc inscriptible.

Lemme

Second théorème de Ptolémée — Soit un quadrilatère inscriptible non croisé $A B C D$ , les longueurs des côtés et des diagonales vérifient la relation :
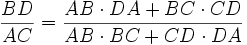
$\frac{BD}{AC}=\frac{AB \cdot DA + BC \cdot CD}{AB \cdot BC + CD \cdot DA}$

Voir aussi

Inégalité de Ptolémée

Théorème de Casey

Liens externes

(fr) Une démonstration du théorème et de sa réciproque sur le site "Descartes et les mathématiques".

Portail de la géométrie

Portail des mathématiques

Ce document provient de « Th%C3%A9or%C3%A8me de Ptol%C3%A9m%C3%A9e ».

Catégories : Théorème de géométrie | Polygone

Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme de Ptolemee de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Théorème de ptolémée — Figure du théorème de Ptolémée. Le théorème de Ptolémée est un théorème de géométrie euclidienne portant sur les diagonales d un quadrilatère. L implication directe est attribuée à l astronome et mathématicien grec Ptolémée, dont il se servit… … Wikipédia en Français
Théorème de Ptolémée — Figure du théorème de Ptolémée. Le théorème de Ptolémée est un théorème de géométrie euclidienne portant sur les diagonales d un quadrilatère. L implication directe est attribuée à l astronome et mathématicien grec Ptolémée, dont il se servit… … Wikipédia en Français
Ptolemee — Ptolémée Pour les articles homonymes, voir Ptolémée (homonymie). Ptolémée Ptolémée d après une gravure allem … Wikipédia en Français
Ptolémée (astronome) — Ptolémée Pour les articles homonymes, voir Ptolémée (homonymie). Ptolémée Ptolémée d après une gravure allem … Wikipédia en Français
Theoreme de Pythagore — Théorème de Pythagore Une version géométrique du théorème. Le théorème de Pythagore est un théorème de géométrie euclidienne qui énonce que dans un triangle rectangle (qui possède un angle droit) le carré de la longueur de l’hypoténuse (côté… … Wikipédia en Français
Théorème de l'hypoténuse — Théorème de Pythagore Une version géométrique du théorème. Le théorème de Pythagore est un théorème de géométrie euclidienne qui énonce que dans un triangle rectangle (qui possède un angle droit) le carré de la longueur de l’hypoténuse (côté… … Wikipédia en Français
Théorème de pythagore — Une version géométrique du théorème. Le théorème de Pythagore est un théorème de géométrie euclidienne qui énonce que dans un triangle rectangle (qui possède un angle droit) le carré de la longueur de l’hypoténuse (côté opposé à l’angle droit)… … Wikipédia en Français
Ptolémée — Pour les articles homonymes, voir Ptolémée (homonymie). Ptolémée Ptolémée d après une gravure allemande du XVIe siècle … Wikipédia en Français
Théorème de Pythagore — Relation entre les longueurs des cô … Wikipédia en Français
Claude Ptolémée — Ptolémée Pour les articles homonymes, voir Ptolémée (homonymie). Ptolémée Ptolémée d après une gravure allem … Wikipédia en Français

Mark and share
Search through all dictionaries
Translate…
Search Internet

Share the article and excerpts