- Axiome des parallèles
-
L'axiome d'Euclide, ou cinquième postulat d'Euclide, est dû au savant Grec Euclide (né vers -325, mort vers -265 à Alexandrie).
C'est un axiome relatif à la géométrie du plan.
La nécessité de cet axiome a constitué la question la plus lancinante de toute l'histoire de la géométrie, et il a fallu plus de deux millénaires de débats presque indiscontinués pour que la communauté scientifique reconnaisse unanimement l'impossibilité de le réduire au statut de simple théorème.
Sommaire
Énoncé initial
Illustration de l'axiome d'Euclide: La droite S détermine les angles internes α et β avec les droites g et h. La somme de ces angles étant inférieure à deux droits, g et h se coupent "du côté de ces deux angles", c'est-à-dire à gauche de S sur la figure.
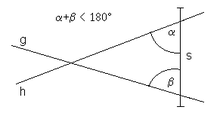
L'énoncé original est exprimé dans le Livre I des Éléments d'Euclide sous la forme suivante[1]:
«Si une droite tombant sur deux droites fait les angles intérieurs du même côté plus petits que deux droits, ces droites, prolongées à l'infini, se rencontreront du côté où les angles sont plus petits que deux droits » (voir figure).
En langage moderne, cela pourrait donner:
« Si une droite coupe deux autres droites en déterminant deux angles internes dont la somme soit différente de deux angles droits, alors les deux droites se coupent dans le demi-plan pour lequel la somme est inférieure à deux angles droits ».
Théorème ou axiome ?
Euclide a présenté cette propriété comme un axiome : son cinquième postulat.
Il est assez vraisemblable que lui même doutait de savoir si son affirmation était ou non démontrable. Ceci est clair autant du choix de la propriété dont l'énoncé est plutôt celui d'un "théorème indémontrable", que du fait qu'Euclide établit les 28 premières propositions de ses Eléments sans recourir à son fameux axiome, comme s'il avait voulu inviter ses lecteurs à s'en passer, et les inciter par là à le démontrer.
De fait, pendant plus de deux millénaires, bien des géomètres ont pensé que cette propriété devait découler logiquement des autres postulats. Ils ont donc tenté de prouver l'axiome d'Euclide. Parmi les plus illustres de ces savants on citera:
- Archimède (IIIe siècle av JC.)
- Posidonios (IIe siècle/Ie siècle av JC.)
- Ptolémée (IIe siècle)
- Proclus (Ve siècle)
- Thabit ibn Qurra (IXe siècle)
- Al-Abbās ibn Said al-Jawharī (IXe siècle)
- Alhazen (Xe siècle/XIe siècle)
- Omar Khayyam (XIe siècle)
Comme la démonstration de l'axiome requerrait de le ramener à des évidences, d'autres énoncés plus ou moins équivalents au postulat d'Euclide ont résulté des meilleures de ces tentatives de démonstration. Les variantes connues sont assez nombreuses. Les plus célèbres sont probablement :- « Par un point donné, on peut mener une et une seule parallèle à une droite donnée ». Cette forme de l'axiome d'Euclide est due au mathématicien Antique Proclus. Elle est connue sous le nom de postulat des parallèles, et sous le nom de postulat de Playfair dans le monde Anglo-Saxon.
- « Il existe des quadrilatères à quatre angles droits»
- « Il existe des triangles dont la somme des angles est égale à deux droits». (Legendre)
- « Il existe des triangles semblables de toutes les tailles». (John Wallis)
- « Par trois points d'un plan, on peut toujours mener un cercle et un seul». (Farkas Bolyai)
- ...
Ces propositions sont considérées comme "grossièrement équivalentes" à l'axiome des parallèles. Par équivalents, il faut comprendre que moyennant des conventions de vocabulaire adaptées, ces axiomes, vrais en géométrie Euclidienne, ne le sont ni en géométrie elliptique ni en géométrie sphérique[2].
Par exemple, les deux axiomes suivants ne sont pas équivalents à l'axiome d'Euclide:
- « Si deux droites non parallèles sont prolongées à l'infini, elles s'écartent indéfiniment».
- « Il existe des droites parallèles»
En effet, ces axiomes vrais en géométrie Euclidienne le sont également en géométrie hyperbolique. Ils ne permettent donc pas de démontrer l'axiome d'Euclide. Cependant, ils sont apparentés à l'axiome d'Euclide, car ils sont faux en géométrie sphérique.
Au XIXe siècle, avec les recherches de Lobatchevski, Bolyai, Gauss, Riemann, Beltrami, Klein, et Poincaré, on a pu trouver d'autres géométries possibles et non-contradictoires en conservant les axiomes de la la géométrie Euclidienne[3] sauf le postulat des parallèles; ces nouvelles géométries sont appelées non-euclidiennes. L'histoire de cette découverte est un épisode fascinant de l'histoire de la géométrie; elle est retracée dans ses grandes lignes à l'article géométrie non euclidienne[4].On trouve deux manières différentes de pratiquer la géométrie sans l'axiome des parallèles.
Dans la première, la somme des angles d'un triangle est supérieure à 180°. On l'appelle (géométrie elliptique (en) ou sphérique). Dans l'autre, elle est inférieure à 180°. C'est la géométrie hyperbolique ou géométrie de Lobatchevski. Par exemple, en modifiant le cinquième axiome ainsi : « Par un point extérieur à une droite, on peut faire passer une infinité de droites parallèles à cette droite, et toutes différentes », on obtient la géométrie hyperbolique.
Dans les géométries non euclidiennes, le théorème de Pythagore n'est plus applicable.
Résistances...
Le postulat d'Euclide est lié à une certaine perception immédiate de l'espace. Y renoncer n'est probablement pas si évident...
Près de 200 ans après les écrits de Lobatchevski, la démarche sur les diverses constructions axiomatiques de la géométrie du plan n'est pas complètement admise ou comprise, comme l'illustrent des tentatives modernes de démonstration de l'axiome, par exemple par Jacques Camü, Démonstration du postulat d'Euclide et de son inutilité, Les presses du midi, 2006 (ISBN 2-87867-063-9).
Dans Les Fous littéraires, page 471, (réédité en 2001, Paris, Éditions des Cendres) (ISBN 2-86742-094-6), l'auteur André Blavier cite 13 ouvrages parus entre 1862 et 1932 écrits par ceux que l'auteur appelle du terme plus général de "quadrateurs" qui pensent démontrer le postulat d'Euclide.
Pour la totalité des scientifiques, l'intérêt de ces démarches ne saurait se trouver que dans le calembourg ou la mystification, ou dans l'analyse des psychopathologies associées.
Notes
- καί έάν είς δύο εύθείας εύθεία έμπίπτουσα τας εντος καί επί τά αύτά μέρη γωνίας δύο όρτων έλάσσονας ποιη έκβαλλομένας τάς δύο εύθείας έπ απειρον συμπίπτειν, έφ ά μέρη έισίν αί των δύο όρτων έλάσσονες
- En toute rigueur, la formulation de son axiome par Euclide est faite de telle sorte qu'elle exclue la géométrie hyperbolique mais pas la géométrie elliptique pour laquelle la question du côté où les droites se rencontrent n'a pas de sens, puisqu'elles se rencontrent de chaque côté. L'unicité du point de rencontre de deux droites est une évidence pour Euclide. La formulation d'Euclide rend dissymétrique, en quelque sorte, l'axiomatique de la géométrie Euclidienne. L'utilisation de l'axiome des parallèles est en ce sens mieux adaptée à l'axiomatique générale de la géométrie. C'est elle qui a été utilisée par D. Hilbert.
- Il n'est pas tout à fait exact qu'on puisse dériver les géométries non-Euclidiennes des 4 autres axiomes d'Euclide que le V°. Ce serait vrai si l'axiomatique d'Euclide ne présentait aucun défaut. Malheureusement tel n'est pas rigoureusement le cas. Malgré sa stupéfiante rigueur, on a trouvé quelques manquements aux autres axiomes d'Euclide. Le problème de l'axiomatique de la géométrie fait encore l'objet de débats de nos jours, mais ces débats ne portent plus sur le 5° axiome dont la compréhension semble clarifiée pour longtemps
- On peut développer des géométries qui diffèrent de celle d'Euclide par bien d'autres choses que le 5° axiome. Ces géométries ne sont bien évidemment pas Euclidiennes non plus. Cependant, le terme "géométrie non-Euclidienne" est consacré aux géométries qui ne diffèrent de celle d'Euclide que par l'absence du postulat des parallèles et par les hypothèses relatives à la taille de l'angle non défini dans le quadrilatère de Sacchieri (voir géométrie non euclidienne).
Articles connexes
- Axiomes de Hilbert : comparaison entre les axiomes d'Euclide et les axiomes de Hilbert
- Géométrie euclidienne
- Géométrie non-euclidienne
- Livre I des Éléments d'Euclide
- Histoire de la géométrie
- Somme des angles d'un triangle
Catégories :- Axiome de la géométrie
- Histoire de la géométrie
Wikimedia Foundation. 2010.
