Hex

Pour les articles homonymes, voir Hex (homonymie).

Hex jeu de société
édition originale de 1952
{{{licence}}}
Auteurs	Piet Hein John Forbes Nash
Éditeur	Parker
Date de 1re édition	1952
Mécanisme	connexion
Joueur(s)	2
Âge	à partir de 7 ans
Durée annoncée	20 minutes
habileté physique  Non  réflexion décision  Oui générateur de hasard  Non info. compl. et parfaite  Oui
modifier

Le jeu de Hex est un jeu de société combinatoire abstrait pour deux joueurs. Il se joue sur un tablier en forme de losange dont les cases sont hexagonales. Toutes les dimensions du côté du losange sont possibles, la plus traditionnelle est celle composée par 11 hexagones, mais on trouve aussi les valeurs 13 ou 19. L'un des inventeurs du jeu John Nash, préconise un tablier de taille 14×14^[1]. Ce jeu possède des similarités avec le go.

Ce jeu, inventé par des mathématiciens fait uniquement appel à la logique, à l'image du go ou des échecs. Son étude est source d'inspiration, non seulement en théorie des jeux, mais aussi pour d'autres branches des mathématiques comme la topologie ou la géométrie algébrique.

Si l'on sait qu'il existe une stratégie gagnante pour le premier joueur, cette stratégie est inconnue si le tablier n'est pas de petite taille (de côté strictement plus petit que 9). La recherche de stratégies efficaces, à défaut d'une stratégie gagnante, est l'objet d'études en intelligence artificielle.

Histoire

Le premier énoncé de la règle du jeu est l'œuvre de Piet Hein lors d'une conférence en 1942 au Parenthesis, l'association des mathématiciens de l'Université de Copenhague. L'auteur cherchait alors à imaginer un jeu équitable, progressif, fini, clair, stratégique et décisif. Le jeu porte alors le nom de Polygone^[2].

En 1948, et de manière indépendante, un jeune mathématicien de l'Université de Princeton du nom de John Nash réinvente le jeu et le diffuse au Fine Hall, une salle commune aux élèves et aux professeurs du département de mathématiques. Il en perçoit l'intérêt en théorie des jeux et démontre l'existence d'une stratégie gagnante pour le premier joueur^[1]. Cependant, sa preuve est non constructive, c’est-à-dire qu'elle n'indique pas de stratégie gagnante^[3]. En 1952, la société Parker Brothers commercialise le jeu aux États-Unis^[2].

Règles du jeu

Convention

Par convention, dans la suite de l'article, le joueur qui joue avec les pions bleus est appelé Bleu, celui qui joue avec les pions rouges, Rouge.

Tablier de Hex 11×11

Configuration gagnante pour Bleu

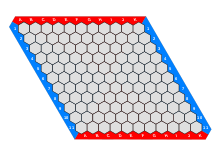
Au début de partie, un tablier vide, illustré sur la figure de gauche, sépare deux joueurs. Ce tablier représente un losange formé par des hexagones réguliers. Chaque joueur est représenté par une couleur, bleu et rouge dans l'article, noir et blanc en général.

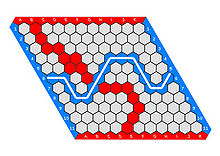
Les joueurs possèdent des pions à leur couleur qu'ils disposent tour à tour sur une case de leur choix et un par un. Le tablier se remplit ainsi progressivement. L'objectif d'un joueur, par exemple Bleu, est de relier les deux côtés opposés du losange symbolisés par la couleur bleue. Si la configuration des pions bleus permet la création d'une ligne continue (en blanc sur la figure) reliant un côté bleu à l'autre, Bleu a gagné et le jeu s'arrête^[4].

Une règle supplémentaire est parfois appliquée^[5]. Si Bleu commence, il joue le premier coup, Rouge a alors le choix entre jouer à son tour ou intervertir les couleurs. Dans le 2ème cas, le joueur qui a commencé devient alors Rouge, et joue alors son premier coup en tant que Rouge, le jeu continuant ensuite normalement. Cela impose de jouer un premier coup ni trop fort (car donnerait un avantage au joueur adverse qui se l'approprierait) ni trop faible (il serait alors laissé par l'adversaire) et réduit l'avantage de commencer.

Stratégie

Un jeu de Hex est nécessairement fini. Dans la configuration 11×11 illustrée sur les figures, il existe 121 cases sur le tablier. Au bout de 61 coups joués d'une part et de 60 de l'autre, le losange est rempli. La suite de l'article montre qu'indépendamment de la manière d'avoir joué, il existe toujours un vainqueur. Le match nul n'existe pas au Hex. La preuve de ce résultat est l'œuvre de Nash^[6]. Pour contrebalancer l'avantage du premier joueur, on peut imaginer un tablier tel que les distances séparant les deux côtés opposés du losange ne soient pas égales. Il est alors simple de montrer que le joueur ayant la plus petite distance à parcourir gagne toujours, et cela indépendamment du fait qu'il commence ou non^[7].

Il existe de nombreux textes sur les différentes stratégies possibles pour gagner^[8]. Cependant les stratégies gagnantes ne sont connues que si le tablier est de dimension restreinte, c'est-à-dire jusqu'à 9×9^[2]. Une autre piste consiste à rechercher des heuristiques sur ordinateur pour jouer le mieux possible, sans rechercher des stratégies nécessairement gagnantes, procédant ainsi comme pour le jeu d'échecs, à l'aide de techniques de programmation issues de l'intelligence artificielle^[9]. Ces programmes sont sources de versions électroniques du jeu^[10].

Jeu de hex et mathématiques

Stratégie et théorie des jeux

Si les rouges ne jouent pas B1 à leur premier coup, ils ne peuvent éviter une défaite en trois coups.

Jouer B1 pour les rouges en deuxième coup ne fait que retarder d'un coup l'inévitable défaite.

En théorie des jeux, le terme de stratégie possède une signification particulière. Une stratégie pour Bleu, s'il commence, indique le premier coup joué, puis le deuxième coup, en fonction du premier coup de Rouge, etc. Une stratégie gagnante assure la victoire quel que soit les choix que fait la partie adverse.

Illustrons ceci par un exemple sur un hex 3×3. Le tablier est numéroté de la manière indiquée sur la figure de gauche. Bleu commence et joue A3 (voir la figure de gauche). On suppose le coup B2 interdit pour commencer, sinon la victoire est trop aisée. Si Rouge ne joue, pour son premier coup, aucune des cases A1, B1 et A2, Bleu joue au deuxième tour A2. Il est alors à un coup de la victoire et il faudrait bloquer deux cases A1 et B1 pour l'en empêcher, ce qui est impossible à réaliser en un coup pour Rouge. Bleu a alors gagné. Le même raisonnement est réalisable sur les cases B1, C1 et B2 : si Rouge joue à son premier coup A1 ou A2, Bleu joue B2 et dispose encore d'une victoire assurée au troisième coup.

L'unique case à jouer en premier coup de Rouge, qui empêche la victoire en trois coups de Bleu, est B1, l'intersection des deux ensembles {A1, B1, A2} et {B1, C1, B2}. Dans ce cas, Bleu joue pour son deuxième coup C1, comme illustré sur la figure de droite. Rouge est maintenant menacé de défaite en un coup. S'il ne joue pas B2 en deuxième coup, Bleu joue B2 en troisième coup et a gagné. Si Rouge joue B2 pour le deuxième coup, Bleu joue C2 pour son troisième coup. Au prochain coup, les cases B3 et C3 lui assurent la victoire. Rouge ne peut bloquer en un unique coup deux cases, il a nécessairement perdu.

Éviter la défaite

La première partie du raisonnement montre que l'adversaire qui commence (supposée Bleu dans cet article) dispose d'une stratégie évitant systématiquement la défaite. La démonstration proposée ici est dite par l'absurde. On suppose le résultat faux, c'est-à-dire que Rouge dispose d'une stratégie gagnante S_r. Bleu construit alors une stratégie S_b qui leur assure la victoire. La stratégie S_b montre que S_r, ne peut être gagnante (il faudrait qu'elle le soit quelle que soit la stratégie adverse). On en déduit que Rouge ne dispose pas d'une stratégie gagnante.

La stratégie S_b consiste à jouer un premier coup à vide, par exemple A1. Ensuite, Bleu vole^[11] la stratégie S_r, en oubliant qu'il a commencé et joué A1. Le deuxième coup de Bleu est donc le premier coup de la stratégie S_r après celui qu'a joué Rouge. Bleu prolonge cette stratégie jusqu'au moment éventuel où il est amené à jouer A1. Il joue alors n'importe quoi, noté α. Il imagine alors que le premier coup oublié était α et qu'il vient de jouer A1. Bleu n'a pas quitté le scénario S_b, consistant à voler la stratégie gagnante. Comme S_r est une stratégie gagnante, la victoire est assurée pour Bleu.

Un tel raisonnement montre qu'une stratégie gagnante S_r ne peut exister. Ce qui montre que quelle que soit la stratégie de Rouge, il est possible d'éviter la défaite. Ce raisonnement ne montre pas que Bleu peut systématiquement gagner, objet du paragraphe suivant, mais uniquement qu'il existe au moins une stratégie S_d qui lui évite toute défaite^[12].

Assurer la victoire

Le paragraphe précédent est un raisonnement de Nash. En 1948, il avait aussi montré l'existence d'une stratégie gagnante pour Bleu. La démonstration proposée ici n'est néanmoins pas de lui mais de David Gale (en)^[13], un camarade d'université à Princeton de Nash^[14]. Elle possède l'avantage d'être plus simple.

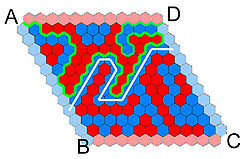
On suppose maintenant que Bleu suit la stratégie S_d. Une fois la partie finie, si le tablier n'est pas entièrement recouvert de pions, l'un des adversaires a nécessairement gagné. Comme cela ne peut être Rouge, c'est Bleu et le résultat est démontré. Sinon, le tablier est entièrement recouvert de pions bleus et rouges et une fois encore, Bleu a nécessairement gagné la partie. Pour s'en rendre compte, on ajoute à chacun des quatre côtés du tablier, un jeu d'hexagones, de la couleur de son joueur. Ces hexagones sont illustrés en clairs sur la figure de droite. Les quatre sommets du nouveau losange sont notés A, B, C et D. Le principe est de construire une ligne, illustrée en vert sur la figure, qui montre la victoire de Bleu. Cette ligne démarre au sommet A, et plus exactement au sommet P₁ commun uniquement à deux hexagones ajoutés et de couleurs distinctes.

La ligne verte suit l'arrête partagée par deux hexagones de couleurs distinctes. Elle se termine sur un autre sommet P₂. On prolonge cette ligne par une nouvelle arrête, différente de P₁P₂ et une fois encore partagée par deux hexagones de couleurs distinctes. On remarque qu'il n'existe qu'un unique choix possible. On répète alors cette même démarche, jusqu'à que cela ne soit plus possible.

Cette ligne verte dispose de quatre propriétés qui montrent la victoire de Bleu. Il est impossible à la ligne verte de faire une boucle, un sommet ne peut être atteint qu'une unique fois par la ligne verte. Le seul motif d'arrêt est que la ligne verte a atteint un sommet extérieur, commun à deux hexagones ajoutés (en clairs sur la figure). Ces deux hexagones sont nécessairement de couleurs différentes, c'est-à-dire qu'ils se trouvent sur un sommet du losange. Comme le sommet A est déjà pris, cette fin se situe sur l'un des sommets B, C ou D. Si l'on parcourt la ligne verte, depuis A jusqu'à sa fin, sur la proximité droite de la ligne, on ne trouve que des hexagones bleus (clairs ou foncés). Sur la proximité gauche, on ne trouve que des hexagones rouges. Cette propriété est illustrée sur la figure.

On suppose que le sommet atteint finalement par la ligne verte est celui noté D. Considérons une deuxième ligne rejoignant par des segments les centres des hexagones constituant le flanc droit de la ligne verte. Cette ligne est intégralement dans la zone bleue. Elle démarre dans la zone bleue claire située entre A et B et finit encore dans le camp bleu, mais cette fois dans la zone claire située entre C et D. Considérons la portion de cette ligne comprise entre le dernier hexagone bleu clair situé entre A et B et le premier hexagone bleu clair situé entre C et D. Cette portion de ligne est illustrée en blanc. Elle est la preuve que Bleu a gagné.

Si d'aventure, la ligne verte se termine sur le sommet B, le même raisonnement que le précédent montre que Rouge a gagné la partie. Cette configuration est impossible avec la stratégie choisie. Cela permet néanmoins de démontrer un résultat un peu plus fort que celui annoncé en début de paragraphe. Si les stratégies de Rouge et Bleu sont quelconques, il existe toujours un vainqueur. Autrement dit, le nul n'existe pas au Hex.

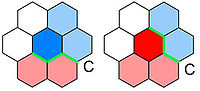
Le sommet C ne peut être atteint par la ligne verte. Pour s'en rendre compte, il suffit d'imaginer que l'hexagone du tablier connexe au sommet C est bleu foncé, illustré sur la figure de gauche. Cet hexagone est nécessairement à gauche de la ligne verte (parcourue dans le sens A vers C), ce qui est impossible car les hexagones situés à gauche de la ligne sont tous rouges. Si le même hexagone est rouge foncé, il est à droite de la ligne verte, ce qui est encore impossible^[15].

Cette démonstration termine la preuve du fait qu'il existe nécessairement une stratégie gagnante pour le premier joueur. En revanche, comme elle utilise un raisonnement par l'absurde, elle ne décrit pas directement de manière de s'y prendre pour effectivement jouer et toujours gagner si l'on commence. Nash exprimait cette idée à D. Gale en 1948 qui le rapporte ainsi : « Un matin, Nash m'a dit qu'il avait un exemple de jeu où il pouvait démontrer que le premier joueur dispose d'une stratégie gagnante, mais qu'il n'avait aucun moyen pour trouver cette stratégie. »^[16]. Il s'avère en fait que le jeu est PSPACE-complet^[17], ce qui modulo certaines hypothèses de théorie de la complexité, signifie que de toute façon la recherche d'une stratégie gagnante devient très rapidement impraticable quand la taille du jeu augmente^[18].

Autres champs mathématiques

Le jeu de Hex est source de démonstrations dans des branches mathématiques éloignées de la théorie des jeux. Le théorème du point fixe de Brouwer indique qu'une fonction continue d'un disque dans lui-même contient toujours un point fixe. Ce résultat se généralise aux dimensions supérieures. Autrement dit, quand on remue son café, il existe toujours un point de la surface qui n'a pas quitté sa position initiale. La démonstration de l'absence de possibilité d'un match nul au jeu de hex est une manière élégante de prouver ce résultat, ce qui constitue l'objet de l'article de David Gale de 1979. Pour être plus précis, ce que David Gale appelle le théorème du jeu de Hex et qui indique l'absence de possible match nul est un résultat équivalent au théorème du point fixe de Brouwer.

Ce théorème a des conséquences amusantes en topologie algébrique, puisqu'on peut l'utiliser pour démontrer le théorème de Jordan^[19], qui indique qu'un lacet simple dans le plan, c'est-à-dire une boucle sans point double, divise l'espace en deux parties connexes, celle intérieure à la boucle qui est bornée et celle extérieure qui ne l'est pas. Ce théorème intuitivement évident est difficile à démontrer rigoureusement. Une conséquence de ce théorème est celui de Poincaré-Bendixson, qui indique qu'une équation différentielle autonome définie par une fonction dérivable à valeurs dans un plan ne peut engendrer de situation chaotique. Cela implique que si un étang est parcouru par un courant qui ne varie pas au cours du temps, un bouchon flottant sur cet étang finit par s'immobiliser ou tourner indéfiniment dans un tourbillon.

Annexes

Références

Liens externes

• T. Maarup Everything You Always Wanted to Know About Hex But Were Afraid to Ask University of Southern Denmark
• Un wiki dédié au Hex.
• Little Golem un site où l'on peut jouer par correspondance au Hex ainsi qu'à d'autres jeux (go, échecs...)
• R. Kirkland Un jeu de Hex7 en ligne par le site Mazeworks

Bibliographie

C. Browne Hex Strategy—Making the Right Connections A. K. Peters, (2000) (ISBN 1568811179)

• Portail des jeux