Calcul de l'effet sagnac en relativité restreinte

Calcul de l'effet sagnac en relativité restreinte: Calcul de l'effet Sagnac en relativité restreinte

Après avoir vu l'effet Sagnac il convient d'en faire une analyse détaillée et rigoureuse dans le cadre de la relativité restreinte.

Sommaire

1 Effet Sagnac

2 Quelques remarques sur la détection par interférométrie de l'effet Sagnac

2.1 Remarque 1

2.2 Remarque 2

3 Calcul du Time Gap

4 Voir aussi

5 Bibliographie

6 Liens externes

Effet Sagnac

Nous allons dériver l'effet Sagnac dans le cadre de la relativité restreinte. Cela nous confirmera le fait que la relativité restreinte prédit bien l'anisotropie de vitesse de la lumière dans le repère tournant, anisotropie de vitesse caractéristique de l'effet Sagnac (décalage des instants d'arrivée sur un émetteur-récepteur E de deux signaux lumineux émis en même temps par E se propageant en sens inverse le long de la circonférence d'un disque tournant). Il pourra aussi être utile au lecteur d'étudier la géométrie de l'espace-temps dans les repères tournants afin d'avoir des détails complémentaires.

Le repère R désignera un repère inertiel avec son origine au centre du disque tournant de rayon $R$ . L'émetteur-récepteur E est situé en un point (noté E) de la périphérie du disque. Il est entrainé en rotation avec le disque. Le repère tournant, attaché au disque, sera noté R'.

Nous appellerons R1 le repère inertiel (local) d'origine située en E et se déplaçant à la même vitesse $V$ que E. Dans le voisinage de E, R' va à la même vitesse que R1 pendant un temps infinitésimal. C'est dans le référentiel inertiel tangent R1 que la vitesse relative de la lumière est isotrope (conformément à la Relativité Restreinte) et non dans le repère tournant R'. La confusion entre vitesse relative de la lumière dans le repère tournant R' (vitesse relative dont la définition repose sur la synchronisation relativiste des horloges distantes ayant cours dans le référentiel inertiel R) et vitesse relative de la lumière dans le référentiel inertiel tangent R1 (vitesse relative dont la définition repose sur la synchronisation relativiste ayant cours dans le référentiel inertiel tangent R1) est à l'origine d'erreurs de raisonnement qui ont, dans le passé, conduit à interpréter à tort l'effet Sagnac comme une mise en défaut de la Relativité Restreinte.

R1, R2, R3... désigneront des repères inertiels tangents allant à la vitesse de R' dans un voisinage infinitésimal d'un point du bord du disque tournant (et pendant une durée infime). Les transformations de Lorentz entre repères inertiels peuvent être utilisées alors que pour traiter le cas de R' dans sa globalité la transformation de Lorentz est inapplicable.

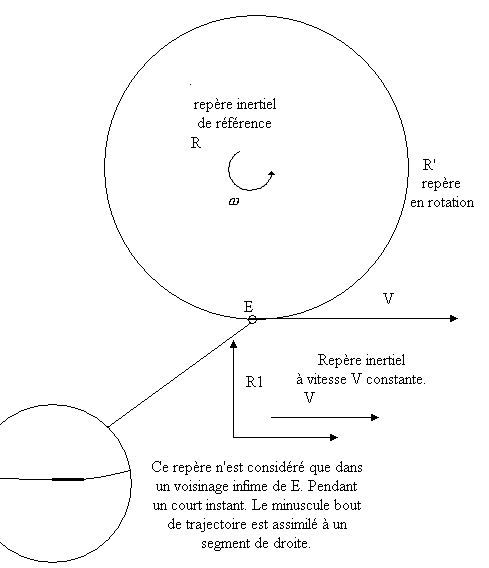
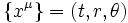Le disque est en rotation avec la vitesse angulaire $ω$ . Le disque étant plat, à deux dimensions, nous choisissons de travailler en coordonnées polaires $\left\{x^\mu\right\}=\left(t,r,\theta\right)$ .

Les coordonnées cartésiennes et polaires sont reliées simplement par :

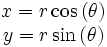
$\begin{matrix}x=r\cos\left(\theta\right)\\y=r\sin\left(\theta\right)\end{matrix}$

L'intervalle relativiste est donné par

$d s 2 = g μν d x μ d x ν = - c 2 d t 2 + d r 2 + r 2 d θ 2$

(ici nous avons noté le "tenseur métrique" $g μν$ car, après le changement de coordonnées, il n'est pas égal au tenseur de Minkowski $η μν$ ). Comme on le vérifie aisément en utilisant le lien entre coordonnées polaires et cartésiennes.

La ligne d'univers de E est donnée par les coordonnées :

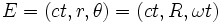
$E=\left(ct,r,\theta\right)=\left(ct,R,\omega t\right)$

C’est-à-dire

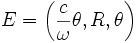
$E=\left(\frac{c}{\omega}\theta,R,\theta\right)$

E émet deux signaux $S 1$ et $S 2$ (pas nécessairement de la lumière) dont les vitesses angulaires sont $ω 1$ (signal dans le même sens que E) et $ω 2$ (signal dans le sens inverse). Leur ligne d'univers est donnée, tout comme ci-dessus, par

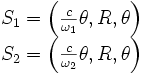
$\begin{matrix}S_1=\left(\frac{c}{\omega_1}\theta,R,\theta\right)\\S_2=\left(\frac{c}{\omega_2}\theta,R,\theta\right)\end{matrix}$

Ce qui nous intéresse est la réception des signaux $S 1$ et $S 2$ par E après un tour complet, c’est-à-dire le moment où les lignes d'univers se recoupent. Ces événements ont lieu aux instants

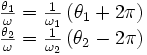
$\begin{matrix}\frac{\theta_1}{\omega}=\frac{1}{\omega_1}\left(\theta_1+2\pi\right)\\\frac{\theta_2}{\omega}=\frac{1}{\omega_2}\left(\theta_2-2\pi\right)\end{matrix}$

La solution de ce système d'équations est

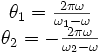
$\begin{matrix}\theta_1=\frac{2\pi\omega}{\omega_1-\omega}\\\theta_2=-\frac{2\pi\omega}{\omega_2-\omega}\end{matrix}$

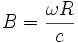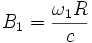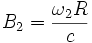Pour alléger l'écriture, nous allons utiliser les vitesses réduites $B=\frac{\omega R}{c}$ , $B_1=\frac{\omega_1R}{c}$ et $B_2=\frac{\omega_2R}{c}$ . Les relations précédentes s'écrivent alors

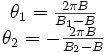$\begin{matrix}\theta_1=\frac{2\pi B}{B_1-B}\\\theta_2=-\frac{2\pi B}{B_2-B}\end{matrix}$ .

Le temps propre est donné par l'intervalle $c d τ = - d s$ . Par conséquent, pour obtenir le temps propre de E, c’est-à-dire le temps lu par E sur l'horloge au repos dans R', il faut intégrer l'intervalle sur sa ligne d'univers (le long de la circonférence du disque, R' s'identifie localement au cours du temps avec les différents repères inertiels tangents notés R1, R2... dans le voisinage de leur origine).

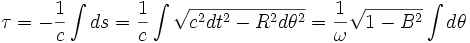
$\tau=-\frac{1}{c}\int ds=\frac{1}{c}\int\sqrt{c^2dt^2-R^2d\theta^2}=\frac{1}{\omega}\sqrt{1-B^2}\int d\theta$

Avec les temps calculés plus haut, nous avons maintenant le temps indiqué par l'horloge de E lors des événements de réception des deux signaux émis par E.

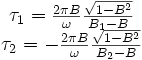
$\begin{matrix}\tau_1=\frac{2\pi B}{\omega}\frac{\sqrt{1-B^2}}{B_1-B}\\\tau_2=-\frac{2\pi B}{\omega}\frac{\sqrt{1-B^2}}{B_2-B}\end{matrix}$

Et la différence est égale à

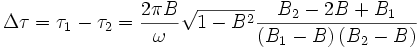
$\Delta\tau=\tau_1-\tau_2=\frac{2\pi B}{\omega}\sqrt{1-B^2}\frac{B_2-2B+B_1}{\left(B_1-B\right)\left(B_2-B\right)}$

On s'intéresse au cas où l'émetteur-récepteur E utilise des signaux dont la vitesse est isotrope dans R1 (comme des signaux lumineux par exemple). Si E émet des particules, il suffit qu'il les émette de la même manière dans les deux directions. Pour de la lumière se propageant dans un milieu où sa vitesse est inférieure à $c$ (de l'eau, une fibre optique), il faut que le milieu se déplace avec E, c’est-à-dire soit solidaire du disque. De même si on utilise des ondes sonores l'air doit donc se déplacer avec le disque (c'est par rapport au milieu de propagation que la vitesse du son est constante).

Pour imposer les vitesses isotropes dans R1, nous avons besoin de connaître les vitesses $B' 1$ et $B' 2$ des signaux dans R1. R et R1 étant des repères inertiels, nous pouvons utiliser l'addition des vitesses et nous avons

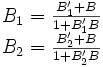
$\begin{matrix}B_1=\frac{B'_1+B}{1+B'_1B}\\B_2=\frac{B'_2+B}{1+B'_2B}\end{matrix}$

En remplaçant dans la différence de temps, nous obtenons

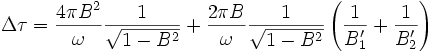
$\Delta\tau=\frac{4\pi B^2}{\omega}\frac{1}{\sqrt{1-B^2}}+\frac{2\pi B}{\omega}\frac{1}{\sqrt{1-B^2}}\left(\frac{1}{B'_1}+\frac{1}{B'_2}\right)$

Nous pouvons maintenant tenir compte de la contrainte d'émission avec une vitesse isotrope

$B' 1 = - B' 2$

La relation précédente devient alors

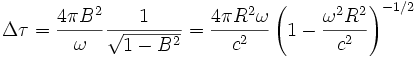
$\Delta\tau=\frac{4\pi B^2}{\omega}\frac{1}{\sqrt{1-B^2}}=\frac{4\pi R^2\omega}{c^2}\left(1-\frac{\omega^2R^2}{c^2}\right)^{-1/2}$

C'est l'effet Sagnac relativiste.

Le calcul de la différence de temps d'arrivée des signaux en E dans R' est donné dans la partie technique. Ce résultat est dérivé en toute généralité puis en supposant que la vitesse des signaux est isotrope dans R1.

Quelques remarques s'imposent.

Ce résultat est bien identique, au premier ordre près (c’est-à-dire en considérant des vitesses angulaires petites), au résultat obtenu dans l'étude simple de l'effet Sagnac obtenu dans un cadre classique. C'est également le résultat obtenu expérimentalement.

Ce résultat montre qu'à grande vitesse il y a une correction relativiste typique.

Même si la vitesse d'émission est isotrope localement dans R1, après un tour complet des signaux, E constate bien un Time Gap donné par la relation dans la partie technique. Ceci confirme l'aptitude de la relativité restreinte à modéliser l'anisotropie de la vitesse de la lumière dans le référentiel tournant.

La vitesse des signaux n'apparaît pas dans l'expression obtenue. L'effet Sagnac est indépendant de la vitesse des signaux (à condition qu'ils soient isotropes) et ne dépend que de la rotation du disque. L'effet Sagnac est universel. C'est prédit par la relativité restreinte et confirmé expérimentalement.

Quelques remarques sur la détection par interférométrie de l'effet Sagnac

Remarque 1

Le Time Gap que nous venons de calculer s'applique aussi aux composantes de Fourier (la décomposition en différentes fréquences) d'un paquet d'onde associé à deux faisceaux de matière (en mécanique quantique, les particules sont aussi des ondes) se propageant dans les deux directions le long de la circonférence avec la même vitesse.

Bien sûr, seuls les flux de matière sont des entités physiques, tandis que les composantes de Fourier sont juste des entités mathématiques qui ne transportent pas d'énergie. Du point de vue de la détection par interférométrie de l'effet Sagnac, le point crucial est le suivant. En dépit de l'absence d'une signification physique directe et du transfert d'énergie, la vitesse de phase de ces composantes de Fourier obéit à la loi de Lorentz de composition des vitesses et est partagée par les composantes de Fourier dans les deux sens.

De plus, la détection par interférométrie de l'effet Sagnac nécessite que le paquet d'onde associé au faisceau de matière soit suffisamment concentré dans l'espace des fréquences pour permettre l'apparition, dans la région d'interférométrie, d'un réseau de franges observables. Il peut être utile de rappeler que :

Le déplacement des franges d'interférence $Δ z$ dépend de la vitesse de phase de la composante de Fourier du paquet d'onde.

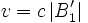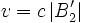Dans un repère inertiel synchronisé avec la méthode d'Einstein, la vitesse de toute composante de Fourier d'un paquet d'onde associé à un faisceau de matière, se déplaçant avec la vitesse (en valeur absolue) $v=c\left|B'_1\right|$ ou $v=c\left|B'_2\right|$ , est donnée par l'expression de de Broglie $v f = v 2 / c$ (mécanique quantique).

Par conséquent, le décalage des franges dans l'effet Sagnac dû à la différence de temps relativiste calculée ci-dessus est :

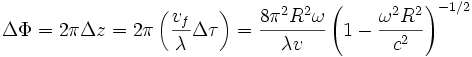
$\Delta\Phi=2\pi\Delta z=2\pi\left(\frac{v_f}{\lambda}\Delta\tau\right)=\frac{8\pi^2R^2\omega}{\lambda v}\left(1-\frac{\omega^2R^2}{c^2}\right)^{-1/2}$

Remarque 2

Notez que Anderson, Stedman et Bilger ont trouvé à l'approximation au premier ordre la différence de temps suivante :

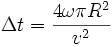
$\Delta t=\frac{4\omega\pi R^2}{v^2}$

et le déplacement des franges suivant :

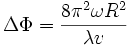
$\Delta\Phi=\frac{8\pi^2\omega R^2}{\lambda v}$

où $v$ est la vitesse "non entraînée" des faisceaux (vitesse dans R).

Bien sûr, cette différence de temps n'est pas en accord avec l'approximation au premier ordre (par rapport à $B = ω R / c$ ) de la valeur que nous avons calculée. Cependant, elle est consistante avec l'approximation au premier ordre de la différence de temps générale (avec des vitesses non nécessairement isotropes) pourvu que 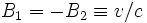$B_1=-B_2\equiv v/c$ : cela représente une situation physique complètement différente où les deux faisceaux sont injectés le long de la circonférence dans des directions opposées avec des vitesses identiques dans le repère inertiel R. La vitesse étant inférieure à $c$ , elle n'est pas invariante et les signaux n'auront pas une vitesse isotrope dans R1.

D'un autre côté, la différence de phase qu'ils donnent et qui est la seule quantité observable dans un dispositif d'interférométrie, n'est pas en accord avec la situation physique considérée par ces auteurs. Mais étonnamment, elle est parfaitement en accord avec l'approximation au premier ordre de la valeur que nous avons calculée. Si la condition d'isotropie dans R1 est imposée, la valeur qu'ils donnent pour le décalage de temps est incorrecte mais la valeur du décalage de phase est correcte.

Calcul du Time Gap

Il est intéressant de dériver le Time Gap d'une autre manière, à la fois plus intuitive et plus simple. Bien qu'elle soit moins rigoureuse (la seule méthode vraiment rigoureuse est celle présentée plus haut).

L'idée est de s'inspirer du décalage constaté lorsque l'on essaie de synchroniser les horloges sur le disque.

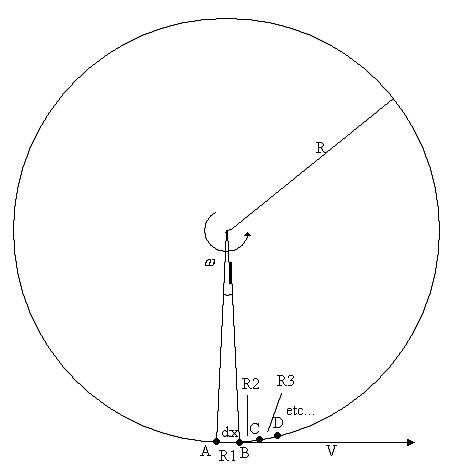
On utilise une série d'observateurs et leurs repères inertiels locaux R1, R2, R3, etc. séparés l'un de l'autre de la distance infinitésimale que nous notons $d x = R d θ$ (où $d θ$ est l'angle infinitésimal qui sépare deux petits domaines successifs).

R est comme d'habitude le repère inertiel.

Chaque observateur est encadré par une paire d'événements : R1 par A et B, R2 par B et C, etc. Les événements sont également séparés (dans R) par la distance $d x$ . Et la vitesse (longitudinale par rapport à $d x$ ) est $V = R ω$ comme d'habitude.

Nous considérons dans R que tous les événements sont simultanés de manière à synchroniser les horloges dans R.

Dans R1, à cause de la relativité de simultanéité, A et B seront décalés.

Si R' était inertiel, il y aurait un décalage uniforme et proportionnel à la distance (voir les transformations de Lorentz), C serait un peu plus décalé que B par rapport à A, D, encore un peu plus, et en faisant un tour complet on aurait un décalage croissant puis décroissant (la coordonnée horizontale de R' dans la figure ci-dessus serait croissante en allant vers la droite de la figure puis décroissante en revenant vers la gauche, en dépassant la position d'origine, puis à nouveau croissante en revenant vers la droite) et un décalage final nul entre A et A !, comme il se doit si la synchronisation ne posait pas de problème. La synchronisation pourrait se faire sur le disque.

Mais sur le disque la synchronisation globale n'est pas possible. Chaque observateur va constater un léger décalage entre les événements qui l'encadre et en un tour complet on obtient un décalage total non nul, c'est le Time Gap autour du disque.

Les transformations de Lorentz donnent le décalage de A et B pour R1 :

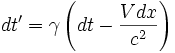
$dt'=\gamma\left(dt-\frac{Vdx}{c^2}\right)$

Puisque A et B sont simultanés dans R, on a $d t = 0$ . Donc,

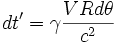
$dt'=\gamma\frac{VRd\theta}{c^2}$

En intégrant sur un tour complet ( $θ$ varie de 0 à $2π$ ), on a le Time Gap

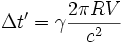
$\Delta t'=\gamma\frac{2\pi RV}{c^2}$

Soit, en utilisant la vitesse réduite $B = V / c$ ,

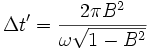
$\Delta t'=\frac{2\pi B^2}{\omega\sqrt{1-B^2}}$

Si l'on emploie la lumière (dans le vide), la vitesse des signaux est $c$ , la différence de longueur parcourue par les deux signaux est donc

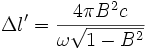
$\Delta l'=\frac{4\pi B^2c}{\omega\sqrt{1-B^2}}$

Qu'on peut qualifier de "Length Gap".

Si on envoie un signal de chaque coté, l'un va subir le Time Gap et l'autre le même Time Gap avec le signe opposé. L'écart de temps entre la réception des signaux sera le double, et on retrouve la formule que nous avons calculée.

En utilisant la vitesse des signaux, on peut aussi calculer la longueur qu'ils parcourent pour O' lorsqu'ils font un tour.

On peut qualifier la différence longueur de "Length Gap". C'est la différence de longueur selon qu'on fait le tour dans un sens ou l'autre. Notez que cela montre bien que la géométrie n'est pas euclidienne dans le repère R'. Pire encore, même avec des géométries courbes habituelles (par exemple la surface de la sphère) que vous fassiez le tour d'un cercle dans un sens ou dans l'autre, cela donne la même longueur. Le découpage en "tranche spatiale" comme suggéré dans l'effet Sagnac avant risque donc non seulement de nous donner un espace courbe mais en plus risque de nous poser des difficultés !

Ce length gap n'est pas « universel », car il dépend de la vitesse du signal. En particulier, si un observateur O' placé sur le disque envoie un « arpenteur » mesurer la longueur de la circonférence à faible vitesse (par rapport à la vitesse de rotation et à $c$ ), selon le sens il mesurera une longueur différente mais avec une différence extrêmement faible.

Le Length Gap calculé ci-dessus est la différence de longueur "maximale".

Un petit exemple numérique donnera une idée. Soit $R = 1$ mètre et $ω = 100000$ (cela fait 16000 tours par seconde, soit presque un million de tours par minute, ce qui est déjà beaucoup, cent fois plus rapide que les moteurs gonflés de la formule 1, et même irréalisable avec des disques réels qui se briseraient sous l'action de la force centrifuge). Supposons que notre arpenteur se déplace à 1 mètre par seconde (sur le disque en rotation).

Alors l'effet Sagnac sera de un centième de milliardième de seconde ! C'est faible mais parfaitement mesurable avec des interféromètres ou même avec des horloges atomiques. Le Length Gap maximal sera de 4 millimètres. Ce qui est mesurable, en particulier par interférométrie. Mais l'arpenteur ne mesurera un Length Gap que d'un centième de nanomètre (plus petit que la taille d'un atome) ! Inutile de faire l'expérience, c'est impossible à mesurer. Même si l'arpenteur, doté d'une horloge, constatera le même Time Gap. Petites causes, grands effets, grandes causes, petits effets !

Voir aussi

L'effet Sagnac

Le paradoxe d'Ehrenfest

Le paradoxe de Selleri

La synchronisation dans les repères tournants

La géométrie de l'espace-temps dans les repères tournants

Le paradoxe des jumeaux et l'effet Sagnac

Les espaces compacts

Le paradoxe des jumeaux dans les espaces compacts

La relativité restreinte

La relativité générale

Le principe de relativité

Le paradoxe des jumeaux

Bibliographie

Le calcul tensoriel en physique. Jean Hladik, Pierre-Emmanuel Hladik. 3^e édition Dunod.

Théorie de la Relativité Restreinte, V. Ougarov, Deuxième Edition, Editions Mir, Moscou. Traduction française Editions Mir, 1979.

Relativité Générale et Gravitation, Edgard Elbaz, Edition Marketing, 1986.

D.E.A. de Physique Théorique - Paris VI, Paris VII, Paris XI, ENS, X, 2003 - 2004, Notes de cours de Relativité Générale, Bernard LINET.

Gravitation. Charles W.Misner, Kip S. Thorne et John Archibald Wheeler. W.H. Freeman and Company, New York.

Stedman G.E., Rep. Prog. Phys., 60, 615 (1997)

Zimmermann J.E. and Mercerau J.E., Phys. Rev. Lett., 14, 887 (1965)

Liens externes

Cours de Relativité Générale. D'après "lectures notes on General Relativity" de Dean M. Caroll. Traduction et adaptation par Jacques Fric Avril 2002.

The relativistic Sagnac effect : two derivations par Guido Rizzi et Matteo Luca Ruggiero

The Curvature of the Relativistic Rotating Disk par Brian Keating

Isotropy of the velocity of light and the Sagnac effect par J.F. Pascual-Sanchez, A. San Miguel et F. Vicente

Références aux données expérimentales sur la relativité

Portail de la physique

Ce document provient de « Calcul de l%27effet Sagnac en relativit%C3%A9 restreinte ».

Catégories : Article à désacadémiser | Relativité

Contenu soumis à la licence CC-BY-SA. Source : Article Calcul de l'effet sagnac en relativité restreinte de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Calcul De L'effet Sagnac En Relativité Restreinte — Après avoir vu l effet Sagnac il convient d en faire une analyse détaillée et rigoureuse dans le cadre de la relativité restreinte. Sommaire 1 Effet Sagnac 2 Quelques remarques sur la détection par interférométrie de l effet Sagnac … Wikipédia en Français
Calcul de l'effet Sagnac en relativite restreinte — Calcul de l effet Sagnac en relativité restreinte Après avoir vu l effet Sagnac il convient d en faire une analyse détaillée et rigoureuse dans le cadre de la relativité restreinte. Sommaire 1 Effet Sagnac 2 Quelques remarques sur la détection… … Wikipédia en Français
Calcul de l'effet Sagnac en relativité restreinte — Après avoir vu l effet Sagnac il convient d en faire une analyse détaillée et rigoureuse dans le cadre de la relativité restreinte. Sommaire 1 Effet Sagnac 2 Quelques remarques sur la détection par interférométrie de l effet Sagnac 2.1 Rema … Wikipédia en Français
Effet Sagnac — L effet Sagnac est un phénomène physique découvert par Georges Sagnac en 1913. C est une asymétrie de la vitesse relative de signaux lumineux parcourant en sens inverse la circonférence d un disque en rotation. Sommaire 1 Introduction et… … Wikipédia en Français
Paradoxe des jumeaux et l'effet sagnac — Le paradoxe des jumeaux et l effet Sagnac est une étude du paradoxe des jumeaux de Langevin dans le cadre des repères en rotation et faisant intervenir l effet Sagnac. Ici, Bernard, au lieu de faire demi tour pendant son voyage effectue un… … Wikipédia en Français
Paradoxe des jumeaux et l'effet Sagnac — Le paradoxe des jumeaux et l effet Sagnac est une étude du paradoxe des jumeaux de Langevin dans le cadre des repères en rotation et faisant intervenir l effet Sagnac. Ici, Bernard, au lieu de faire demi tour pendant son voyage effectue un… … Wikipédia en Français
Histoire de la relativité restreinte — L’histoire de la relativité restreinte décrit le développement de propositions et constatations empiriques et conceptuelles, au sein de la physique théorique, qui ont permis d’aboutir à une nouvelle compréhension de l’espace et du temps. Cette… … Wikipédia en Français
Espace Compact En Relativité — En relativité restreinte, un espace compact ou espace fermé est un espace fini et sans bord. Pour avoir une idée qualitative de cette notion, penser au jeu vidéo Pac Man : chaque plan dans lequel se déplace Pac Man est « fermé », c … Wikipédia en Français
Espace compact en relativite — Espace compact en relativité En relativité restreinte, un espace compact ou espace fermé est un espace fini et sans bord. Pour avoir une idée qualitative de cette notion, penser au jeu vidéo Pac Man : chaque plan dans lequel se déplace Pac… … Wikipédia en Français
Espace compact en relativité — En relativité restreinte, un espace compact ou espace fermé est un espace fini et sans bord. Pour avoir une idée qualitative de cette notion, penser au jeu vidéo Pac Man : chaque plan dans lequel se déplace Pac Man est « fermé », c … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Calcul de l'effet sagnac en relativité restreinte

Calcul de l'effet Sagnac en relativité restreinte

Sommaire

Effet Sagnac

Quelques remarques sur la détection par interférométrie de l'effet Sagnac

Remarque 1

Remarque 2

Calcul du Time Gap

Voir aussi

Bibliographie

Liens externes

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Calcul de l'effet sagnac en relativité restreinte

Calcul de l'effet Sagnac en relativité restreinte

Sommaire

Effet Sagnac

Quelques remarques sur la détection par interférométrie de l'effet Sagnac

Remarque 1

Remarque 2

Calcul du Time Gap

Voir aussi

Bibliographie

Liens externes

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link