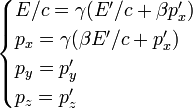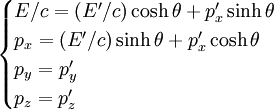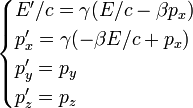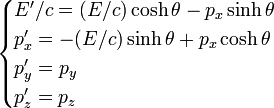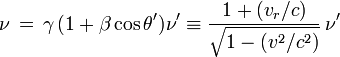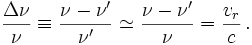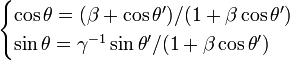- Relativité restreinte (formulaire)
-
Formulaire de relativité restreinte
Cet article fait partie de la série
formulaire de physiqueOptique Électro- Magnéstatique Physique quantique Thermodynamique Mécanique des fluides Mécanique Relativité restreinte Trou noir Analyse vectorielle Les notations
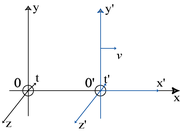
Les formules établissent le passage entre les coordonnées (t, x ) d'un événement dans le repère inertiel fixe, disons celui de la Terre, et les coordonnées (t ’, x ’ ) du même événement dans le repère mobile, disons de la fusée, laquelle se déplace le long de l'axe des x avec la vitesse v.
On suppose que les origines du temps coïncident à
On pose :
Le paramètre angulaire
Pour simplifier les formules il est utile d'introduire le paramètre angulaire défini par les formules suivantes :
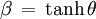 soit
soit 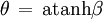
À l'aide de ce paramètre on peut écrire :
L'invariant de la relativité restreinte
La quantité suivante est invariante dans un changement de coordonnées
et définit le temps propre
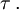
Les transformations de Lorentz
ce qui donne sous forme matricielle (plus facile à visualiser):
En utilisant les fonctions hyperboliques de l'angle θ, on obtient des expressions analogues aux formules de changement d'axes de coordonnées par rotation plane :
En sens inverse
ou
La dilatation du temps
Si l'horloge de la fusée mesure la durée
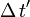 entre deux événements se produisant dans cette fusée, donc séparés par une distance spatiale
entre deux événements se produisant dans cette fusée, donc séparés par une distance spatiale 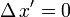 , la durée mesurée dans le laboratoire fixe de la Terre est
, la durée mesurée dans le laboratoire fixe de la Terre estLa durée mesurée dans un repère extérieur est toujours plus grande que la durée propre.
La contraction des longueurs
Si la fusée est de longueur L’ dans son propre repère, sa longueur L mesurée par la distance entre les deux points de la Terre en coïncidence avec l'avant et l'arrière de la fusée au même instant (sur Terre), donc correspondant à
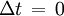 , est donnée par
, est donnée parLa longueur mesurée sur Terre est plus petite que la longueur propre de la fusée.
Loi de composition des vitesses
Un obus est tiré dans la fusée avec une vitesse w ’ par rapport au repère de cette fusée, dans la direction du mouvement. La vitesse w de l'obus par rapport à la Terre est
En utilisant les paramètres angulaires
on a la loi additive
Le quadrivecteur énergie-impulsion
Comme
on a
Aux faibles vitesses
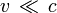
On a toujours la relation
La quantité suivante est invariante dans un changement de repère
Pour un photon, m = 0 et
Énergie cinétique
L'énergie cinétique d'une particule est
Pour
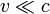
et pour
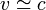
Formules de changement de repère
Ce sont les formules de Lorentz
ou
Transformations inverses
ou
Effet Doppler-Fizeau
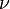 étant la fréquence reçue sur Terre,
étant la fréquence reçue sur Terre, 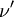 la fréquence émise par la source,
la fréquence émise par la source, 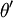 l'angle que fait le photon avec l'axe Ox dans le repère de cette source,
l'angle que fait le photon avec l'axe Ox dans le repère de cette source, 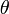 l'angle avec l'axe Ox dans le repère terrestre,
l'angle avec l'axe Ox dans le repère terrestre, 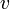 la vitesse de la source par rapport à la Terre et
la vitesse de la source par rapport à la Terre et 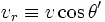 la vitesse radiale, on a
la vitesse radiale, on aAux faible vitesses
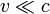
Si l'étoile s'éloigne, v est positif, cosθ' est négatif,
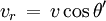 est négatif, de sorte que la fréquence diminue (la longueur d'onde augmente, c'est le décalage vers le rouge).
est négatif, de sorte que la fréquence diminue (la longueur d'onde augmente, c'est le décalage vers le rouge).Phénomène d'aberration de la lumière :
Articles connexes
- Portail de la physique
Catégorie : Relativité
Wikimedia Foundation. 2010.

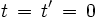
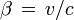
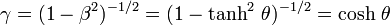
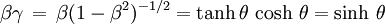
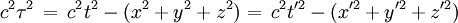
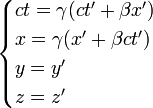
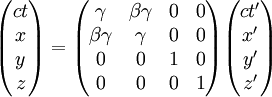
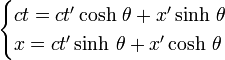
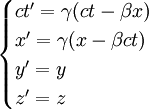
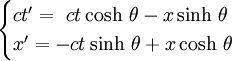
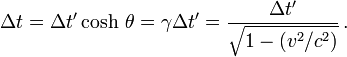
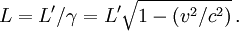
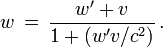

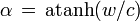
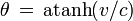
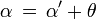
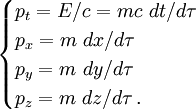
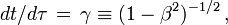
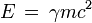
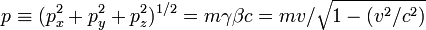
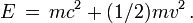
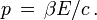
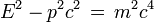
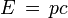
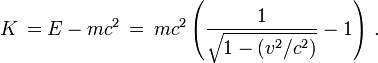
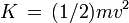
![K \simeq E \simeq pc = \frac{mc^2}{\sqrt{2(1-\beta)}}\equiv \frac{mc^2}{\sqrt{2[1-(v/c)]}}\,.](/pictures/frwiki/97/acc25fffc50d7155b19484633067d1eb.png)