Nombre Narcissique

Nombre Narcissique: Nombre narcissique

Un nombre narcissique n est un entier naturel pour lequel il existe un entier positif ou nul p tel que la somme de chacun des chiffres de n mis à la puissance p est égale à n.

Mathématiquement : Soit 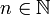$n\in\mathbb{N}$ . On définit le i-uplet d'entiers naturels $[\![x_1;x_i]\!], i\in\mathbb{N^*}, x_i \neq 0$ tel que $n=\sum_{j=1}^i~10^{j-1} x_j=\overline{x_i x_{i-1}...x_1}$ . n est dit narcissique si et seulement si $\exists p \in\mathbb{N^*} | n=\sum_{j=1}^i~x_j^p$ .

Inuitivement, il est clair que si i augmente, p tend à augmenter. Ci-dessous la démonstration.

Démonstration

Soit $n=\sum_{j=1}^i~10^{j-1} x_j.$ Comme $x_i\neq 0$ , $n\ge 10^{i-1}$ . D'autre part, $\forall j, x_j \le 9$ . Donc $\sum_{j=1}^i~x_j^p \leq 9^p i$ .

D'où n narcissique $\Longrightarrow 9^p i \ge 10^{i-1}$ . Par théorème de croissance comparée, il vient que pour un i donné, p est nécessairement au-dessus d'un rang donné, qui croît avec i.

Remarque : Cela ne prouve pas pour autant l'existence de p !

Exemples :

$153 = 1 3 + 5 3 + 3 3$ $548834 = 5 6 + 4 6 + 8 6 + 8 6 + 3 6 + 4 6$

Cas particuliers :

$\forall p \in\mathbb{N^*}$ , 0 est narcissique pour p.

Un nombre narcissique pour p=3 est dit nombre d'Armstrong.

Par extension, on parle aussi de nombre narcissique pour un entier qui peut être découpé en tranches égales d'un ou de plusieurs chiffres et dont la somme de ces tranches, élevée à une puissance entière naturelle, est égale à lui-même.

Exemples :

$3025 = (30 + 25) 2$ $4913 = (4 + 9 + 1 + 3) 3$

Portail des mathématiques

Ce document provient de « Nombre narcissique ».

Catégorie : Propriété décimale

Contenu soumis à la licence CC-BY-SA. Source : Article Nombre Narcissique de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

Nombre narcissique — Un nombre narcissique (ou nombre d Armstrong de première espèce, ou en anglais PPDI, pour pluperfect digit invariant)[1] est un entier naturel n non nul qui est égal à la somme des puissances p ièmes de ses chiffres en base dix, où p désigne le… … Wikipédia en Français
Narcissique — Narcissisme Le narcissime désigne l amour de soi ou l importance excessive accordée à l image de soi. Sommaire 1 En psychiatrie 2 En psychanalyse 3 Origine mythologique 4 Narcissisme et socié … Wikipédia en Français
153 (nombre) — Cet article est relatif au nombre 153. Pour l année, voir 153. 153 (nombre) Cardinal Cent cinquante trois Ordinal Cent cinquante troisième 153e Préfixe grec … Wikipédia en Français
313 (nombre) — Cardinal Trois cent treize Ordinal Trois cent treizième 313e Adverbe Trois cent treizièmement … Wikipédia en Français
Narcissisme — Le narcissisme est le fondement de la confiance en soi. Lorsqu il est défaillant, le terme peut désigner l importance excessive accordée à « l image » de soi. Le dictionnaire commun le définit comme « contemplation de soi ou… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Coïncidence mathématique — En mathématiques, une coïncidence mathématique est une expression de quasi égalité entre deux quantités, sans qu’il y ait une explication théorique directe. Sommaire 1 Introduction 2 Quelques exemples 2.1 Formules avec π 2.2 … Wikipédia en Français
Jean Laplanche — (né en 1924), philosophe de formation, est un psychanalyste « de la troisième génération ». L importance de son œuvre se mesure à l aune de l avancée scientifique que propose la psychanalyse en France après Freud : les travaux de… … Wikipédia en Français
Rorscha — Test de Rorschach La première planche parmi les dix du test de Rorschach Le test de Rorschach ou psychodiagnostik est un outil d évaluation psychologique de type projectif élaboré par le psychiatre et psychanalyste Hermann Rorschach en 1921. Il… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Nombre Narcissique

Nombre narcissique

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Nombre Narcissique

Nombre narcissique

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link