- Loi exponentielle
-
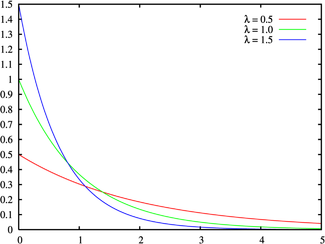
Exponentielle Densité de probabilité / Fonction de masse
Fonction de répartition
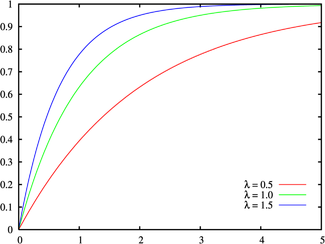
Paramètres  intensité ou inverse de l'échelle (réel)
intensité ou inverse de l'échelle (réel)Support 
Densité de probabilité (fonction de masse) λe − λx Fonction de répartition 1 − e − λx Espérance 
Médiane (centre) 
Mode 
Variance 
Asymétrie 
Kurtosis normalisé 
Entropie 
Fonction génératrice des moments 
Fonction caractéristique 
modifier 
Une loi exponentielle correspond au modèle suivant:
X est une variable aléatoire définissant la durée de vie d'un phénomène. Si l'espérance de vie du phénomène est E(X) et si la durée de vie est sans vieillissement, c'est-à-dire si la durée de vie au-delà de l'instant T est indépendante de l'instant T, alors X a pour densité de probabilité :
- f(t) = 0 si t < 0
 pour tout t ≥ 0.
pour tout t ≥ 0.
On dit que X suit une loi exponentielle de paramètre

De façon plus formelle on peut caractériser la loi exponentielle de la façon suivante:

Une loi à valeurs dans
 qui vérifie cette propriété est alors exponentielle et toute loi exponentielle vérifie cette probabilité. Cette propriété traduit l'absence de mémoire de la loi exponentielle. Par exemple, la probabilité qu'un phénomène se produise entre les temps t et t+s s'il ne s'est pas produit avant est la même que la probabilité qu'il se produise entre les temps 0 et s. On peut oublier l'instant de départ pour modéliser la probabilité. Cette caractérisation est importante car elle permet de montrer que certains phénomènes peuvent être modélisés par une distribution exponentielle. Cette loi permet entre autres de modéliser la durée de vie de la radioactivité ou d'un composant électronique.
qui vérifie cette propriété est alors exponentielle et toute loi exponentielle vérifie cette probabilité. Cette propriété traduit l'absence de mémoire de la loi exponentielle. Par exemple, la probabilité qu'un phénomène se produise entre les temps t et t+s s'il ne s'est pas produit avant est la même que la probabilité qu'il se produise entre les temps 0 et s. On peut oublier l'instant de départ pour modéliser la probabilité. Cette caractérisation est importante car elle permet de montrer que certains phénomènes peuvent être modélisés par une distribution exponentielle. Cette loi permet entre autres de modéliser la durée de vie de la radioactivité ou d'un composant électronique.Sommaire
Calcul de P(X > t)
Si on appelle F(t) la probabilité que la durée de vie soit supérieure à t, le fait que la durée de vie soit sans vieillissement se traduit par l'égalité suivante :

Puisque la fonction F est monotone et bornée, cette équation implique que F est une fonction exponentielle. Il existe donc k réel tel que pour tout t :
F(t) = ekt. Notons que k est négatif, puisque F est inférieure à 1. La densité de probabilité f est définie, pour tout t ≥ 0, par :
f(t) = − kekt. Le calcul de l'espérance de X, qui doit valoir E(X) conduit à l'équation:

On calcule l'intégrale en intégrant par parties ; on obtient :

Donc

et

Espérance, variance, écart type, médiane
 Densité d'une durée de vie d'espérance 10 de loi exponentielle ainsi que sa médiane.
Densité d'une durée de vie d'espérance 10 de loi exponentielle ainsi que sa médiane.
Si X est une variable aléatoire qui suit une loi exponentielle de paramètre λ
Nous savons, par construction, que l'espérance de X est
 .
.On calcule la variance en intégrant par parties ; on obtient :
 .
.L'écart type est donc
 .
.La médiane, c'est-à-dire le temps T tel que P(X>T) = 0,5, est
 .
.Champ d'application
Un domaine privilégié de la loi exponentielle est le domaine de la radioactivité (Rutherford et Soddy). Chaque atome radioactif possède une durée de vie qui suit une loi exponentielle. Le paramètre λ s'appelle alors la constante de désintégration.
La durée de vie moyenne
 s'appelle le temps caractéristique.
s'appelle le temps caractéristique.La loi des grands nombres permet de dire que la concentration d'atomes radioactifs va suivre la même loi. La médiane
 correspond au temps T nécessaire pour que la population passe à 50% de sa population initiale et s'appelle la demi-vie ou période.
correspond au temps T nécessaire pour que la population passe à 50% de sa population initiale et s'appelle la demi-vie ou période.On modélise aussi fréquemment la durée de vie d'un composant électronique par une loi exponentielle.
Durée de vie minimale
Si les variables aléatoires X, Y sont indépendantes et suivent deux lois exponentielles de paramètres λ, μ, alors Z = inf(X; Y) est une variable aléatoire qui suit la loi exponentielle de paramètre λ + μ.
Cette observation est très utile pour déterminer l'espérance de vie d'un système constitué de deux composants en série.
Lien avec la loi géométrique
La loi géométrique est une version discrétisée de la loi exponentielle. En conséquence, la loi exponentielle est une limite de lois géométriques renormalisées.
Propriété — Si
 suit la loi exponentielle d'espérance 1, et si
suit la loi exponentielle d'espérance 1, et si  alors
alors  suit la loi géométrique de paramètre
suit la loi géométrique de paramètre Démonstration
Démonstration![\begin{align}
\mathbb{P}(Y=k)
&=
\mathbb{P}(\lceil\theta X\rceil=k)
\\
&=
\mathbb{P}(\theta X\in]k-1,k])
\\
&=
\mathbb{P}\left(X\in\left]\tfrac{k-1}{\theta},\tfrac{k}{\theta}\right]\right)
\\
&=
F_X\left(\tfrac{k}{\theta}\right)-F_X\left(\tfrac{k-1}{\theta}\right)
\\
&=
\exp\left(-\ \tfrac{k-1}{\theta}\right)-\exp\left(-\ \tfrac{k}{\theta}\right)
\\
&=
\left(e^{-\ \tfrac{1}{\theta}}\right)^{k-1}\ \left(1-e^{-\ \tfrac{1}{\theta}}\right).
\end{align}](a/c3a5bfb4ff2287f0dfc0d2342f6baf02.png)
Notons que, pour un nombre réel

 désigne la partie entière supérieure de
désigne la partie entière supérieure de  définie par
définie par
En choisissant

on fabrique ainsi, à partir d'une variable aléatoire exponentielle
 de paramètre
de paramètre  une variable aléatoire
une variable aléatoire
suivant une loi géométrique de paramètre
 arbitraire (avec toutefois la contrainte
arbitraire (avec toutefois la contrainte  ), car
), car  suit alors une loi exponentielle de paramètre 1 (et d'espérance 1).
suit alors une loi exponentielle de paramètre 1 (et d'espérance 1).Réciproquement,
Propriété — Si, pour
 la variable aléatoire
la variable aléatoire  suit la loi géométrique de paramètre
suit la loi géométrique de paramètre  , et si
, et si
alors
 converge en loi vers la loi exponentielle de paramètre
converge en loi vers la loi exponentielle de paramètre  Démonstration
DémonstrationOn se donne une variable aléatoire exponentielle
 de paramètre 1, et on pose
de paramètre 1, et on pose
Alors
 et
et  ont même loi, en vertu de la propriété précédente. Par ailleurs, pour tout
ont même loi, en vertu de la propriété précédente. Par ailleurs, pour tout 

Or d'une part la convergence presque sûre entraine la convergence en loi, d'autre part la loi de
 est la loi exponentielle de paramètre
est la loi exponentielle de paramètre 
On peut voir ces différentes convergences comme de simples conséquences de la convergence du schéma de Bernoulli vers le processus de Poisson.
Voir aussi
- Portail des probabilités et des statistiques
Wikimedia Foundation. 2010.
