Intégrale de Riemann

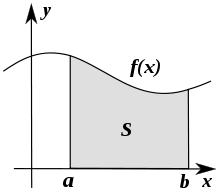
Interprétation géométrique de l'intégrale de la fonction

f

En analyse réelle, l'intégrale de Riemann^[1] est une façon simple de définir l'intégrale d'une fonction sur un intervalle. En termes géométriques, cette intégrale s'interprète comme l'aire du domaine sous la courbe représentative de la fonction, comptée algébriquement.

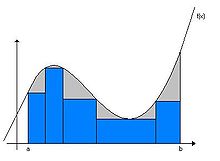
Le procédé général utilisé pour définir l'intégrale de Riemann est l'approximation par des fonctions en escalier, pour lesquelles la définition de l'aire sous la courbe est aisée. Les fonctions pour lesquelles cette définition est possible sont dites intégrables au sens de Riemann. C'est le cas notamment des fonctions continues, continues par morceaux, ou réglées sur un segment $[a, b]$ .

On obtient un procédé d'intégration plus général et plus satisfaisant, notamment vis-à-vis du passage à la limite, en introduisant l'intégrale de Lebesgue ou l'intégrale de Kurzweil-Henstock.

Sommaire

1 Définition de l'intégrale
2 Comparaison avec d'autres procédés d'intégration
3 Voir aussi
4 Notes et références

Définition de l'intégrale

Les fonctions en escalier

Aire sous une courbe approchée par une suite de rectangles

Article détaillé : fonction en escalier.

Soit $E$ un sous-ensemble quelconque du segment $[a, b]$ . Soit $χ E$ la fonction qui vaut 1 si $x$ appartient à $E$ et 0 sinon. $χ E$ est appelée la fonction indicatrice ou fonction caractéristique de $E$ .

Ces fonctions sont notre point de départ et nous posons :

pour tout segment $[c, d]$ inclus dans $[a, b]$ et pour toute constante $z\geq 0$ ,

$\int z \chi_{[c,d]}(x)\,\mathrm dx = z(d-c)$

Dans ce cas l'aire sous la courbe de cette fonction est égale à l'aire du rectangle de base $[c, d]$ et de hauteur $z$ .

De la même manière, quelques expérimentations géométriques avec de telles fonctions nous amènent à penser que si $f 1, f 2,..., f n$ sont $n$ fonctions indicatrices sur des intervalles disjoints et si $a 1, a 2,..., a n$ sont des scalaires positifs, alors l'aire du domaine sous la courbe de la fonction

$f=a_1 f_1+a_2 f_2+\dots+a_n f_n$

doit être égale à

$\int f = a_1 \int f_1 + a_2 \int f_2 + \dots + a_n \int f_n$

Une fonction de cette forme, c'est-à-dire une combinaison linéaire de fonction indicatrices, est dite fonction en escalier. Remarquons maintenant que nous avons décidé quelle devrait être l'intégrale d'une fonction en escalier à valeurs positives. Il est naturel, dans le cas où certains des $a 1, a 2,..., a n$ sont négatifs, de décider que la formule ci-dessus doit être adoptée comme définition de $\textstyle\int f$ . Cela signifie que nous comptabilisons avec un signe moins les aires en dessous de l'axe des $x$ .

Dans la formule ci-dessus l'écriture $f = a 1 f 1 + a 2 f 2 + ... + a n f n$ n'est pas tout à fait unique (on peut toujours découper un intervalle en plus petits intervalles). Peut-on obtenir une valeur différente de $\textstyle\int f$ en décomposant $f$ de deux manières différentes ?

On peut montrer que non: il est possible, d'une manière unique, d'associer à toute fonction en escalier une intégrale de sorte que pour n'importe quelle combinaison linéaire de fonctions en escalier $f = a 1 g 1 + a 2 g 2 + ... + a n g n$ on ait $\textstyle\int f = a_1 \int g_1 + a_2 \int g_2 + \dots + a_n \int g_n$ , et telle que lorsque $f$ est la fonction indicatrice d'un intervalle alors $\textstyle\int f$ soit la longueur de cet intervalle.

Une différence importante entre l'intégrale de Riemann et celle de Lebesgue, est que dans cette dernière on y remplace les fonctions en escalier par les fonctions étagées qui sont des combinaisons linéaires finies de fonctions indicatrices d'ensembles qui ne sont pas nécessairement des intervalles. La longueur de l'intervalle est remplacée par la mesure de l'ensemble.

Intégrales inférieure et supérieure

À partir de l'interprétation géométrique, nous imposons que si $f$ vérifie $f(x)\leqslant g(x)$ pour tout $x$ de $[a, b]$ , alors

$\int f \leqslant \int g$

Nous appelons cette propriété la croissance de l'intégrale (on remarque qu'elle impose de donner une valeur négative à l'intégrale d'une fonction négative).

L'intégrale d'une fonction en escalier étant définie et la condition de monotonie étant imposée, nous pouvons essayer d'intégrer des fonctions bornées arbitraires. Soit $f$ une fonction à valeurs réelles définie sur $[a, b]$ et soit $l$ une fonction en escalier telle que pour tout $x$ on ait, $l(x)\leqslant f(x)$ (cela n'est donc possible que si $f$ est bornée inférieurement). De plus, soit $u$ une fonction en escalier telle que pour tout $x$ on ait, $u(x)\geqslant f(x)$ (une telle $u$ ne peut exister que si la fonction est bornée supérieurement). Si nous devions donner une valeur à $\textstyle\int f$ conforme à la condition de monotonie, alors nous devrions avoir :

$\int l \leqslant \int f \leqslant \int u$

L'intégrale $\textstyle\int l$ est alors appelée une somme inférieure pour $f$ et l'intégrale $\textstyle\int u$ est alors appelée une somme supérieure pour f. L'inégalité précédente doit être vérifiée pour toutes sommes supérieures et inférieures de $f$ , donc nous pouvons en déduire une autre inégalité :

$\sup_l\int l\leqslant\int f\leqslant \inf_u\int u$

où $\textstyle\sup_l\int l$ est la borne supérieure de toutes les sommes inférieures, et $\textstyle\inf_u\int u$ est la borne inférieure de toutes les sommes supérieures. Le nombre $\textstyle\sup_l\int l$ est parfois appelé intégrale inférieure de $f$ ; de la même manière, le nombre $\textstyle\inf_u\int u$ est appelé intégrale supérieure.

Il peut arriver que l'intégrale supérieure ne soit pas égale à l'intégrale inférieure. Par exemple, pour la fonction indicatrice $χ Q$ où $Q$ est l'ensemble des nombres rationnels du segment $[a, b]$ avec $a < b$ , l'intégrale inférieure est égale à 0 et l'intégrale supérieure est égale à $b - a > 0$ .

Si les intégrales supérieures et inférieures sont égales, alors on dit que la fonction est intégrable au sens de Riemann ou Riemann-intégrable. Son intégrale $\textstyle\int f$ est cette valeur commune. Dans le contexte de cet article, nous dirons intégrable ou non intégrable sachant que nous parlons d'« intégrabilité » au sens de Riemann.

Définition directe de l'intégrabilité au sens de Riemann

La définition originale par Riemann de son intégrale^[2] utilisait les sommes de Riemann, mais nous présentons ici l'approche ultérieure^[3], équivalente, par les sommes de Darboux.

La discussion précédente nécessitait une notion préalable d'intégrale pour les fonctions en escalier, et par exemple on a accepté sans démonstration la propriété de monotonie pour les fonctions en escalier.

Afin de faire l'économie d'une discussion préalable des fonctions en escalier, il est préférable de procéder en toute généralité de la manière suivante (qui est très proche de l'approche originelle de Riemann lui-même). Soit $f$ une fonction bornée définie sur l'intervalle borné $[a, b]$ . À toute subdivision $σ = (a = x 0 < x 1 < ... < x n = b)$ on associe son pas $\delta(\sigma) = \max_{1\leq i \leq n} (x_{i} - x_{i-1})$ , qui mesure sa finesse, ainsi que les nombres réels suivants $M i$ et $m i$ , pour $i=1,\dots,n$

$M_i= \sup_{x\in [x_{i-1} ,x_i]} f(x)$

$m_i= \inf_{x\in [x_{i-1} ,x_i]} f(x)$

puis, les sommes de Darboux supérieure et inférieure :

${K(\sigma)} = \sum_{i=1}^n M_i(x_{i} - x_{i-1})$

${J(\sigma)} = \sum_{i=1}^n m_i(x_{i} - x_{i-1})$

$\Delta(\sigma) = K(\sigma) - J(\sigma)\geq 0$

On dit que $f$ est intégrable au sens de Riemann sur $[a, b]$ s'il est possible de trouver des subdivisions rendant les écarts $Δ(σ)$ entre sommes supérieure et inférieure arbitrairement petits.

On prouve alors qu'il existe un nombre réel unique, noté $\textstyle\int \limits_a^b f(x)\mathrm dx$ , qui a la propriété suivante :

$\lim \delta(\sigma_k)=0\implies\lim_{k\to+\infty} J(\sigma_k)=\lim_{k\to+\infty} K(\sigma_k) = \int \limits_a^b f(x)\,\mathrm dx$

pour n'importe quelle suite de subdivisions $σ k$ dont les pas $δ(σ k)$ tendent vers zéro^[2].

On peut établir qu'une fonction en escalier est bien intégrable en ce sens et que l'intégrale ainsi définie pour elle a toutes les propriétés (linéarité, monotonie) espérées. Et notre définition est alors en toute généralité équivalente avec celle de la section précédente.

Propriétés

Lemme 1 — Soit $[a, b]$ un segment. L'application $\textstyle I :f \to\int f$ qui associe à $f$ l'intégrale de $a$ à $b$ est une forme linéaire. Et ainsi pour toutes fonctions intégrables $f$ et $g$ , et tout nombre réel $λ$ , $I (λ f + g) = λ I (f) + I (g)$ .

Ceci peut être démontré à partir des premiers principes de la construction de l'intégrale de Riemann.

Théorème 2 — Toute fonction à valeurs réelles, continue sur le segment $[a, b]$ est intégrable.

La preuve repose sur le fait qu'une fonction continue sur un segment est uniformément continue.

Corollaire 3 — Si $f$ est continue sur $[a, b]$ sauf peut-être en un nombre fini de points de discontinuité, et si $f$ est bornée, alors $f$ est intégrable.

La condition $f$ bornée ne peut pas être omise.

Théorème 4 — Toute fonction croissante sur le segment $[a, b]$ est intégrable. Idem pour les fonctions décroissantes. Plus généralement une fonction monotone par morceaux est intégrable.

Une fonction croissante peut avoir une infinité de discontinuités, et n'est donc pas nécessairement continue par morceaux, donc ce Théorème n'est pas une conséquence du précédent. Sa démonstration est d'ailleurs nettement plus facile, elle découle très directement de la définition avec les sommes supérieures et inférieures donnée plus haut.

Théorème 5 — Si $(f k)$ est une suite de fonctions intégrables sur $[a, b]$ , et si $(f k)$ converge uniformément vers une fonction $f$ , alors $f$ est intégrable, et les intégrales $\textstyle\int f_k$ convergent vers $\textstyle\int f$ .

Corollaire 6 — Soit $C (a, b)$ l'espace de Banach des fonctions continues sur $[a, b]$ muni de la norme de convergence uniforme. Alors $\textstyle I :f\to\int f$ est continue. Conjointement avec le lemme 1, nous pouvons en déduire que l'intégrale est une forme continue sur $C (a, b)$ .

Les hypothèses du Théorème 5 (convergence uniforme sur un segment) sont très fortes. Une difficulté avec l'intégrale de Riemann se pose, lorsque nous tentons d'amoindrir ces hypothèses. Car en fait, la suite numérique $\textstyle(\int f_k)$ converge vers le nombre $\textstyle\int f$ plus souvent que le théorème ne le suggère (il suffit que la convergence soit dominée), mais pour le démontrer il faut des raisonnements nettement moins simples que ceux définissant l'intégrale de Riemann et donnant ses propriétés de base. Il est néanmoins possible^[4] de le prouver avec les notions de base sur les suites et les séries de nombres réels.

Critère de Lebesgue pour l'intégrabilité de Riemann — Soit $f$ une fonction définie et bornée sur $[a, b]$ et soit $D$ l'ensemble des discontinuités de f sur $[a, b]$ . Alors $f$ est Riemann-intégrable si, et seulement si, $D$ a une mesure de Lebesgue nulle.

Comme exemple de fonction avec un ensemble non dénombrable de discontinuités et cependant Riemann-intégrable, on a (fonction caractéristique de l'ensemble de Cantor) :

$f(x) = \begin{cases} 1, & \mbox{si } x \in C\\ 0, & \mbox{si } x \notin C \end{cases}$

où C est l'ensemble de Cantor.

Un autre aspect de l'intégrale de Riemann est qu'elle ne concerne dans un premier temps que les fonctions bornées, sur un intervalle borné. Il faut une deuxième définition si l'une de ces conditions n'est pas vérifiée. Par exemple, si nous souhaitons intégrer une fonction $f$ de $-\infty$ à $+\infty$ , en supposant qu'elle soit intégrable sur tout intervalle borné, on prendra la limite suivante, qui peut d'ailleurs, ou non, exister:

$\lim_{a\to-\infty \atop b\to+\infty} \int_{a}^b f(x)\mathrm dx$

Dans le cadre de l'intégration au sens de Lebesgue il n'y a qu'une seule définition et par exemple $\textstyle\int_0^\infty e^{-x}\,\mathrm dx$ est une intégrale de Lebesgue au sens strict tandis que comme intégrale de Riemann elle est une intégrale généralisée. De même pour $\textstyle\int_0^1 \frac1{\sqrt x}\,\mathrm dx$ . Cependant les intégrales au sens de Lebesgue sont toujours automatiquement absolument convergentes. Ainsi, l'intégrale $\textstyle\int_0^{+\infty} \frac{\sin(x)}x\,\mathrm dx$ n'est ni une intégrale de Riemann au sens propre, ni une intégrale de Lebesgue, mais elle est une intégrale généralisée de Riemann (ou de Lebesgue), et sa valeur est $π / 2$ . En désignant par $f (x)$ la somme de $\frac{\sin(x)}x$ et de la fonction indicatrice des rationnels positifs on voit que $\textstyle\int_0^{+\infty} f(x)\,\mathrm dx$ donne un exemple d'une intégrale de Lebesgue généralisée (on dit aussi impropre) qui n'existe pas en tant qu'intégrale de Riemann. Sa valeur est encore $π / 2$ .

Comparaison avec d'autres procédés d'intégration

Voir aussi

Notes et références

↑ L'intégrale de Riemann aété introduite dans l'article de Bernard Riemann "Über die Darstellbarkeit einer Function durch eine trigonometrische Reihe" (Sur la représentabilité d'une fonction par une série trigonométrique). Ce travail a été présenté à l'Université de Göttingen en 1854 comme Habilitationsschrift de Riemann (qualification pour devenir enseignant). Il a été publié en 1868 dans Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen (Actes de la Société Royale Philosophique de Göttingen), vol. 13, pages 87-132. (Consultable en ligne à: Google Books). Pour la définition de Riemann de son intégrale, voir la section 4, "Über der Begriff eines bestimmten Integrals und den Umfang seiner Gültigkeit" (Sur le concept d'une intégrale définie et le domaine de sa validité), pages 101-103.
↑ ^{a et b} Notes d'un cours de DEUG à l'université de Lille reproduisant le texte de Riemann
↑ G. Darboux, « Mémoire sur les fonctions discontinues », dans Ann. Sci. E.N.S., vol. 4, 1875, p. 57-112
↑ Document pdf de Jean-François Burnol

Portail de l'analyse

Catégories :

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Intégrale de Riemann de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Integrale de Riemann — Intégrale de Riemann Interprétation géométrique de l intégrale de la fonction f. En analyse réelle, l intégrale de Riemann est une façon simple de définir l intégrale d une fonction sur un intervalle. En termes géométriques, cette intégrale s… … Wikipédia en Français
Intégrale De Riemann — Interprétation géométrique de l intégrale de la fonction f. En analyse réelle, l intégrale de Riemann est une façon simple de définir l intégrale d une fonction sur un intervalle. En termes géométriques, cette intégrale s interprète comme l aire … Wikipédia en Français
Intégrale de riemann — Interprétation géométrique de l intégrale de la fonction f. En analyse réelle, l intégrale de Riemann est une façon simple de définir l intégrale d une fonction sur un intervalle. En termes géométriques, cette intégrale s interprète comme l aire … Wikipédia en Français
Intégrale de Riemann-Stieltjes — Intégrale de Stieltjes Thomas Stieltjes (1856–1894) L intégrale de Stieltjes constitue une généralisation de l intégrale ordinaire, ou intégrale de Riemann. En effet, considérons deux fonctions réelles bornées f … Wikipédia en Français
Integrale de Lebesgue — Intégrale de Lebesgue En mathématiques, on appelle intégrale de Lebesgue à la fois une théorie de l intégration d une fonction selon une mesure quelconque et le cas particulier d intégration d une fonction définie sur les réels, , munis de la… … Wikipédia en Français
Intégrale De Lebesgue — En mathématiques, on appelle intégrale de Lebesgue à la fois une théorie de l intégration d une fonction selon une mesure quelconque et le cas particulier d intégration d une fonction définie sur les réels, , munis de la mesure de Lebesgue (ou… … Wikipédia en Français
Intégrale de lebesgue — En mathématiques, on appelle intégrale de Lebesgue à la fois une théorie de l intégration d une fonction selon une mesure quelconque et le cas particulier d intégration d une fonction définie sur les réels, , munis de la mesure de Lebesgue (ou… … Wikipédia en Français
RIEMANN (B.) — Après la mort de Georg Friedrich Bernhard Riemann, son œuvre fut publiée en un seul volume, y compris les fragments posthumes, et cette brièveté ne tient pas seulement à la fin précoce du mathématicien: d’une part, ses démonstrations sont très… … Encyclopédie Universelle
Integrale de Stieltjes — Intégrale de Stieltjes Thomas Stieltjes (1856–1894) L intégrale de Stieltjes constitue une généralisation de l intégrale ordinaire, ou intégrale de Riemann. En effet, considérons deux fonctions réelles bornées f … Wikipédia en Français
Intégrale De Stieltjes — Thomas Stieltjes (1856–1894) L intégrale de Stieltjes constitue une généralisation de l intégrale ordinaire, ou intégrale de Riemann. En effet, considérons deux fonctions réelles bornées f … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Intégrale de Riemann

Sommaire