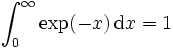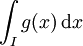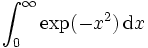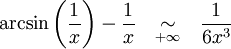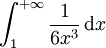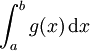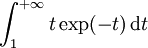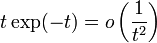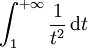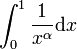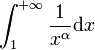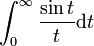- Integrale impropre
-
Intégrale impropre
En mathématiques, l'intégrale impropre désigne une extension de l'intégrale usuelle, définie par une forme de passage à la limite dans des intégrales. On note en général les intégrales impropres sans les distinguer des véritables intégrales ou intégrales définies, ainsi
est un exemple très classique d'intégrale impropre convergente, mais qui n'est pas définie au sens de l'intégration usuelle (que ce soit l'intégration des fonctions continues par morceaux, l'intégrale de Riemann, ou celle de Lebesgue).
Dans la pratique, on est amené à faire une étude de convergence d'intégrale impropre
- lorsqu'on intègre jusqu'à une borne infinie,
- lorsqu'on intègre jusqu'à une borne en laquelle la fonction n'admet pas de limite finie,
- lorsqu'on englobe un point de non définition dans l'intervalle d'intégration.
Dans chaque cas, on évaluera l'intégrale définie comme une fonction d'une des deux bornes et on prendra la limite de la fonction obtenue lorsque l'argument tend vers la valeur de la borne.
L'intégrale impropre partage un certain nombre de propriétés élémentaires avec l'intégrale définie. Elle ne permet pas d'écrire des résultats d'interversion limite-intégrale avec les théorèmes d'interversion de convergence uniforme. Par contre, il existe un théorème d'interversion limite-somme adapté aux intégrales impropres : c'est le théorème de convergence dominée.
Sommaire
Définition
Définition de la convergence d'une intégrale impropre
Soit
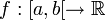 une fonction continue. Si la limite
une fonction continue. Si la limiteexiste et est finie, on appelle cette limite intégrale impropre de f sur [a,b[.
De la même manière, soit
![f : ]a, b] \rightarrow \mathbb{R}](/pictures/frwiki/101/e90f9f06ae5de904857a494265c7cdbe.png) une fonction continue. Si la limite
une fonction continue. Si la limiteexiste et est finie, on appelle cette limite intégrale impropre de f sur ]a,b].
Dans les deux cas on peut noter cette limite de la manière suivante :
Si la limite existe et est finie on dit que
 converge, sinon on dit qu'elle diverge.
converge, sinon on dit qu'elle diverge.Remarques :
- On peut généraliser facilement la définition à des fonctions qui sont continues seulement sur ]a,b[. On dit alors que
-
- converge lorsque pour un
![c \in ]a,b[](/pictures/frwiki/48/0eff8d69467c10b57a87a34915f5b2bd.png) arbitraire, les intégrales
arbitraire, les intégrales
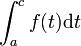 et
et 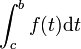
- convergent.
- Il existe une autre notation qui permet d'expliciter le caractère impropre de l'intégrale.
-
- peut s'écrire
- Si f est en fait continue sur le segment [a,b], on obtient par ces définitions la même valeur que si on calculait l'intégrale définie de f.
Définition de l'intégrabilité d'une fonction
Soit I = (a,b) un intervalle quelconque de
 et
et  une fonction continue par morceaux sur I. On dit que f est intégrable sur I si et seulement si
une fonction continue par morceaux sur I. On dit que f est intégrable sur I si et seulement siconverge. On dit que l'intégrale de f sur I converge absolument.
Si l'intégrale de f converge absolument sur I, alors l'intégrale de f sur I converge. La réciproque est fausse. Une fonction dont l'intégrale converge tout en étant pas absolument convergente est appelée intégrale semi-convergente.
Autres propriétés
Intégration par parties
L'intégration par parties est une technique, parmi tant d'autres, permettant de calculer une intégrale définie. Pour les intégrales impropres, cette technique peut être également utilisée. Mais il faut faire attention à la définition des "objets obtenus". Si
existe, ce n'est pas forcément le cas pour
![\left[ f(x) g(x) \right]_{a}^{b}](/pictures/frwiki/97/a38e6d8cf563ac08f448ea395af6df5c.png) ou pour
ou pour 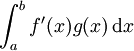
Donc si on cherche à calculer par exemple l'intégrale
on peut écrire :
avec a < X < b puis on effectue un passage à la limite en faisant
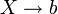 . On observe alors que si les termes
. On observe alors que si les termes![\left[ f(x) g(x) \right]_{a}^{\to b}](/pictures/frwiki/99/cfb4f47098f98491f578b12433d1de0a.png) et
et 
sont définis, l'intégration par parties est possible.
Linéarité des intégrales impropres
La linéarité des intégrales impropres est possible mais requiert la même condition que pour l'intégration par parties : les "objets obtenus" doivent être définis. Ainsi on peut écrire
car les intégrales
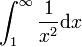 et
et 
sont convergentes.
Mais par contre, l'intégrale
ne peut être scindée car les intégrales
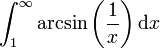 et
et 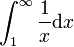
sont divergentes.
Techniques pour établir la convergence d'une intégrale impropre
Par passage à la limite
Pour calculer une intégrale du type
on choisit X tel que a < X < b. On calcule ensuite l'intégrale
 comme une intégrale classique. Enfin on effectue un passage à la limite pour faire tendre X vers b, ce qui nous amène au résultat.
comme une intégrale classique. Enfin on effectue un passage à la limite pour faire tendre X vers b, ce qui nous amène au résultat.Par exemple, calculons
Pour
 on a
on aPar passage à la limite, on obtient
Majoration
Soit I un intervalle. On cherche à montrer que
est convergente. Si on arrive à trouver une fonction g telle que pour tout
 ,
, 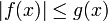 et telle que
et telle quesoit convergente, alors
est convergente.
Par exemple, prenons l'intégrale de Gauss
Pour tout
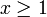 ,
, 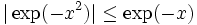 et
etest convergente, donc
est convergente.
Équivalence
On considère les intégrales impropres
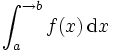 et
et 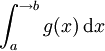
Si f et g sont équivalentes au voisinage de b et de signe constant, alors les 2 intégrales ci-dessus sont de même nature.
Par exemple, prenons
Pour trouver l'équivalence de arcsin(1 / x) − 1 / x en
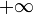 , il faut effectuer un développement limité en 0 pour la variable 1 / x (ce qui équivaut à un développement limité en
, il faut effectuer un développement limité en 0 pour la variable 1 / x (ce qui équivaut à un développement limité en 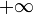 pour la variable x). On a
pour la variable x). On adonc
et tout est positif (de signe constant). Par un calcul de primitive, on obtient que
est convergente. Donc
est convergente.
Négligeabilité
On considère les intégrales impropres suivantes
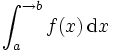 et
et 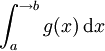
Si f(x) = o(g(x)) au voisinage de b et si
est convergente, alors
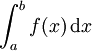 est convergente.
est convergente.Par exemple, prenons
On a
donc
Or
est convergente donc
est convergente.
Exemples classiques
Intégrale de Riemann
L'intégrale
converge si et seulement si α < 1.
L'intégrale
converge si et seulement si α > 1.
Intégrale de Bertrand
L'intégrale
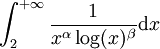 converge si et seulement si α > 1 ou (α = 1 et β > 1).
converge si et seulement si α > 1 ou (α = 1 et β > 1).Intégrale de Dirichlet
L'intégrale
est semi-convergente.
- Portail des mathématiques
Catégorie : Théorie de l'intégration
Wikimedia Foundation. 2010.

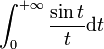
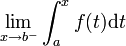
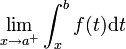
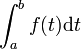
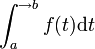
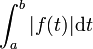
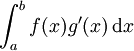
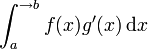
![\int_{a}^{X} f(x) g'(x)\,\mathrm dx = \left[ f(x) g(x) \right]_{a}^{X} - \int_{a}^{X} f'(x) g(x) \,\mathrm dx](/pictures/frwiki/48/0009d95db2b92e0b17992c29fd30ba29.png)
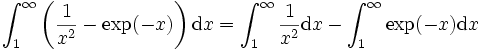
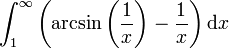
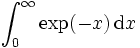
![\int_{0}^{X} \exp(-x)\,\mathrm dx = \left[ -\exp(-x) \right]_{0}^{X} = 1 - \exp(-X)](/pictures/frwiki/51/37b9da14fa9422d9d3e885d9b4542cf9.png)