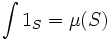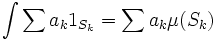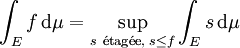Intégrale de lebesgue

Intégrale de Lebesgue

En mathématiques, on appelle intégrale de Lebesgue à la fois une théorie de l'intégration d'une fonction selon une mesure quelconque et le cas particulier d'intégration d'une fonction définie sur les réels, $\mathbb{R}$ , munis de la mesure de Lebesgue (ou sur $\mathbb{R}^n$ ). Il existe d'autres théories de l'intégration.

L'intégrale de Lebesgue joue un rôle important en analyse, en théorie des probabilités et dans beaucoup d'autres domaines des mathématiques.

Dans les cas simples, l'intégrale d'une fonction positive $f$ peut être vue comme l'aire comprise entre l'axe des $x$ (l'axe horizontal) et la courbe de la fonction $f$ . La construction de l'intégrale de Lebesgue peut être étendue à un ensemble beaucoup plus complet de fonctions, définies sur des espaces plus généraux que $\mathbb{R}$ ou $\mathbb{R}^n$ .

Sommaire

1 Un intérêt pratique de l'intégrale de Lebesgue
2 Historique
3 Construction formelle
4 Théorèmes
5 Voir aussi
- 5.1 Notes
- 5.2 Articles connexes

Un intérêt pratique de l'intégrale de Lebesgue

Après la construction de l'intégrale de Cauchy-Riemann, on s'est intéressé à étendre le théorème fondamental du calcul intégral:

« Soit f une fonction réelle sur l'axe réel, continue par morceaux. Alors pour tout intervalle fermé [a,b], f est Riemann-intégrable, admet une primitive continue sur [a,b] et, si F désigne une primitive de f sur [a,b], on a pour tout x dans [a,b]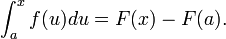 $\int_a^x f(u) du = F(x)-F(a).$ »

cependant les études faites sur l'intégrale de Riemann aboutissent au théorème suivant qui est le meilleur qu'on sache démontrer:

« Si F est différentiable sur [a,b] et si F' est Riemann-intégrable sur [a,b], alors pour tout x dans [a,b]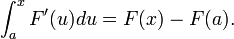 $\int_a^x F'(u) du = F(x)-F(a).$ »

Mais malheureusement, il existe des fonctions F qui sont dérivables sur [a,b] sans que cette dérivée soit Riemann-intégrable.

L'objectif premier de l'intégrale de Lebesgue est de lever cette restriction et on obtient alors l'énoncé

« Si F est différentiable sur [a,b] et si F' est bornée sur [a,b], alors F' est Lebesgue-intégrable sur [a,b], et pour tout x dans [a,b]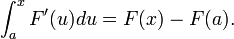 $\int_a^x F'(u) du = F(x)-F(a).$ »

Par la suite, on a trouvé plusieurs autres constructions (intégrale de Denjoy, Perron, Henstock, Khintchine, ...) d'une intégrale qui satisfont alors à l'énoncé

« Si F est différentiable sur [a,b], alors F' est intégrable sur [a,b], et pour tout x dans [a,b]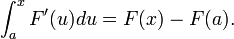 $\int_a^x F'(u) du = F(x)-F(a).$ »

Historique

Avant Henri Lebesgue, la théorie de l'intégration s'appuyait sur l'intégrale de Riemann, mais celle-ci était plutôt insatisfaisante pour diverses raisons : problème de définition efficace des intégrales dites impropres, difficulté à établir des théorèmes de convergence...

En créant son intégrale, Lebesgue l'a lui-même comparée à l'intégrale de Riemann : « Imaginez que je doive payer une certaine somme ; je peux sortir les pièces de mon porte-monnaie comme elles viennent pour arriver à la somme indiquée, ou sortir toutes les pièces et les choisir selon leur valeur. La première méthode est l'intégrale de Riemann, la deuxième correspond à mon intégrale. » Pour expliquer cette phrase, on peut préciser que l'intégration de Riemann « parcourt » le segment et mesure la « hauteur » de la fonction au fur et à mesure, tandis que l'intégrale de Lebesgue considère la « taille » des ensembles de niveau {f = y}.

Cette théorie s'est avérée particulièrement féconde. Elle a permis (via la théorie des tribus) de formaliser les probabilités, de définir de nombreux espaces fonctionnels extrêmement importants et a marqué le début de la théorie de la mesure.

Construction formelle

Soit μ une mesure positive sur une σ-algèbre X au-dessus d'un ensemble E. (En analyse réelle, E désigne l'espace euclidien de dimension n, 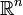$\mathbb R^n$ ou des sous-ensembles de celui-ci mesurables au sens de Lebesgue; X désigne la sigma-algèbre de tous les sous-ensembles de E mesurables au sens de Lebesgue, et μ la mesure de Lebesgue. En probabilité et en statistique, μ est une probabilité sur un espace probabilisable E.) Nous construisons l'intégrale des fonctions à valeurs réelles définies sur E de la manière suivante :

Soit S une partie de X et soit f la fonction définie sur E qui vaut 0 en dehors de S et 1 sur S (i.e., f(x) = 1 si x est dans S, f(x) = 0 sinon.) Cette fonction est appelée fonction indicatrice ou fonction caractéristique de S et est notée 1_S.

Pour donner une valeur à ∫1_S conforme à la mesure donnée μ, on pose raisonnablement :

$\int 1_S = \mu (S)$

Nous étendons par linéarité à l'espace vectoriel engendré par les fonctions indicatrices :

$\int \sum a_k 1_{S_k} = \sum a_k \mu( S_k)$

où la somme est finie et les coefficients a _k sont des nombres réels. Une telle combinaison linéaire finie de fonctions indicatrices s'appelle une fonction étagée. Remarquons qu'une fonction étagée peut être écrite de plusieurs façons comme une combinaison linéaire de fonctions caractéristiques, mais l'intégrale sera toujours la même.

Maintenant les difficultés commencent quand nous tentons de passer à la limite pour pouvoir intégrer des fonctions plus générales. Quelles sont les limites de fonctions étagées et peut-on définir leur intégrale ? Le procédé suivant fonctionne et contourne le problème.

Soit f une fonction positive définie sur E (nous lui permettons d'atteindre la valeur + ∞, en d'autres termes, f prend des valeurs dans la droite réelle achevée.) Nous définissons ∫f comme étant la borne supérieure de ∫s où s varie dans l'ensemble de toutes les fonctions étagées qui sont inférieures à f (c'est-à-dire que pour tout x, s(x) ≤ f(x).) Cette définition est analogue à celle des sommes inférieures de Riemann. Cependant, nous ne construirons pas de somme supérieure, et ce fait est important pour obtenir une classe plus générale de fonctions intégrables. Pour être plus explicite, on peut mentionner la mesure et le domaine d'intégration:

$\int_E f\,\mathrm d\mu = \sup_{s~\mathrm{\acute{e}tag\acute{e}e},\; s \le f} \int_E s\,\mathrm d\mu$

Vous pouvez vous demander si cette définition a un sens (est-ce que les fonctions étagées gardent la même intégrale ?) Vous pouvez aussi vous demander si ceci correspond dans tous les cas à la même notion d'intégrale de Riemann. Il n'est pas du tout difficile de prouver que la réponse aux deux questions est oui.

Nous avons défini ∫f pour toute fonction positive définie sur E; cependant pour certaines fonctions, ∫ f sera infinie. De plus, les propriétés attendues d'addition et de limite des intégrales ne sont pas satisfaites, à moins que nous n'exigions que toutes nos fonctions soient mesurables, i.e. que la pré-image (ou image réciproque) de tout intervalle soit dans X. Nous ferons dorénavant cette hypothèse.

Pour traiter les fonctions signées, nous avons besoin de définitions supplémentaires. Si f est une fonction mesurable sur l'ensemble E à valeurs réelles (ou ± ∞), alors nous pouvons écrire f = g - h où g(x) = (f(x) si f(x)>0, 0 sinon) et h(x) = (-f(x) si f(x) <0, 0 sinon). Remarquons que les deux fonctions g et h sont positives. Aussi remarquons que |f| = g + h. Si ∫|f| est finie, alors f est dite intégrable au sens de Lebesgue ou sommable. Dans ce cas, les deux intégrales ∫g et ∫h sont finies, et cela a un sens de définir ∫f par ∫g - ∫h.

Les fonctions à valeurs complexes peuvent être intégrées de la même manière, en considérant la partie réelle et la partie imaginaire séparément.

Théorèmes

Toute notion d'intégrale doit raisonnablement être linéaire et monotone, et l'intégrale de Lebesgue possède ces propriétés: si f et g sont des fonctions intégrables et a et b sont des nombres réels, alors af + bg est intégrable et ∫(af + bg) = a∫f +b∫g; si f ≤ g, alors ∫f ≤ ∫g.

Deux fonctions qui diffèrent seulement sur un ensemble de mesure μ nulle ont la même intégrale, ou plus précisément: si μ({x : f(x) ≠ g(x)}) = 0, alors f est intégrable si et seulement si g est intégrable, et dans ce cas ∫ f = ∫ g.

L'un des avantages les plus importants que l'intégrale de Lebesgue procure par rapport à l'intégrale de Riemann est la facilité avec laquelle nous pouvons passer à la limite. Nous allons donner ici trois des théorèmes les plus utilisés:

Le théorème de convergence monotone déclare que si (f _k) est une suite de fonctions mesurables positives telles que pour tout k, f_k(x) ≤ f_k+1(x) et si f = lim f_k, alors la suite de terme général ∫f_k converge vers ∫f (remarque: ∫f peut être infinie ici).

Le lemme de Fatou déclare que si (f _k) est une suite de fonctions mesurables positives et si f = liminf f_k, alors ∫f ≤ liminf ∫f_k (à nouveau, ∫f peut être infinie).

Le théorème de convergence dominée déclare que si (f _k) est une suite de fonctions mesurables de limite ponctuelle f, et s'il existe une fonction intégrable g telle que pour tout k, |f _k| ≤ g, alors f est intégrable et la suite de terme général ∫f_k converge vers ∫f.

Voir aussi

Notes

Regardez d'autres dictionnaires:

Integrale de Lebesgue — Intégrale de Lebesgue En mathématiques, on appelle intégrale de Lebesgue à la fois une théorie de l intégration d une fonction selon une mesure quelconque et le cas particulier d intégration d une fonction définie sur les réels, , munis de la… … Wikipédia en Français
Intégrale De Lebesgue — En mathématiques, on appelle intégrale de Lebesgue à la fois une théorie de l intégration d une fonction selon une mesure quelconque et le cas particulier d intégration d une fonction définie sur les réels, , munis de la mesure de Lebesgue (ou… … Wikipédia en Français
Intégrale de Lebesgue — En mathématiques, l’intégrale de Lebesgue désigne à la fois une théorie relative à l intégration et à la mesure, puis le résultat de l intégration d une fonction à valeurs réelles définie sur (ou sur ), munis de la mesure de Lebesgue.… … Wikipédia en Français
LEBESGUE (H.) — Le mathématicien Henri Lebesgue est l’un des fondateurs de l’analyse moderne. Presque tous ses travaux se rattachent à la théorie des fonctions de variables réelles. Sa conception de l’intégration et de la mesure renouvelle l’étude des problèmes… … Encyclopédie Universelle
Integrale de Riemann — Intégrale de Riemann Interprétation géométrique de l intégrale de la fonction f. En analyse réelle, l intégrale de Riemann est une façon simple de définir l intégrale d une fonction sur un intervalle. En termes géométriques, cette intégrale s… … Wikipédia en Français
Intégrale De Riemann — Interprétation géométrique de l intégrale de la fonction f. En analyse réelle, l intégrale de Riemann est une façon simple de définir l intégrale d une fonction sur un intervalle. En termes géométriques, cette intégrale s interprète comme l aire … Wikipédia en Français
Intégrale de riemann — Interprétation géométrique de l intégrale de la fonction f. En analyse réelle, l intégrale de Riemann est une façon simple de définir l intégrale d une fonction sur un intervalle. En termes géométriques, cette intégrale s interprète comme l aire … Wikipédia en Français
Intégrale de Riemann — Interprétation géométrique de l intégrale de la fonction f. En analyse réelle, l intégrale de Riemann[1] est une façon simple de définir l intégrale d une fonction sur un … Wikipédia en Français
Intégrale de Kurzweil-Henstock — En mathématiques, et plus précisément en analyse, l intégrale de Kurzweil Henstock (ou KH intégrale, ou intégrale de jauge) a été mise au point dans les années 1950 dans le but de présenter une théorie de l intégration à peine plus compliquée à… … Wikipédia en Français
Intégrale de Daniell — En mathématiques, l intégrale de Daniell est un type d intégration qui généralise le concept plus élémentaire de l intégrale de Riemann qui est généralement la première enseignée. Une des principales difficultés de la formulation traditionnelle… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Intégrale de lebesgue