Theoreme de convergence dominee

Theoreme de convergence dominee: Théorème de convergence dominée

Le théorème de convergence dominée est un des théorèmes principaux de la théorie de l'intégration de Lebesgue.

Sommaire

1 Le théorème de convergence dominée

2 Généralisation

3 Exemple d'application

4 Voir aussi

Le théorème de convergence dominée

Théorème — Soit 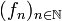$(f_{n})_{n \in \mathbb{N}}$ une suite de fonctions mesurables sur un espace mesuré 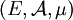$(E,\mathcal A,\mu)$ , à valeurs dans $\mathbb R$ ou $\mathbb C$ telle que :

La suite de fonctions 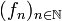$(f_{n})_{n \in \mathbb{N}}$ converge simplement vers une fonction 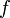$f \;$ sur $E$ .

Il existe une fonction 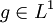$g \in L^1$ telle que :

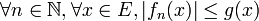
$\forall n \in \mathbb N, \forall x \in E, |f_{n}(x)|\leq g(x)$
Alors 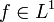$f \in L^1$ et
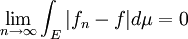
$\lim_{n \to \infty} \int_E |f_n-f|d\mu= 0$
ce qui entraîne :
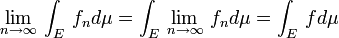
$\lim_{n \to \infty}\, \int_{E}{\, f_{n}d\mu}= \int_{E}{\, \lim_{n \to \infty}\, f_{n}d\mu} = \int_{E}{\, f}d\mu$

La démonstration de ce théorème repose principalement sur le lemme de Fatou.

Démonstration

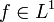Commençons par montrer que $f \in L^1$ :

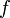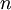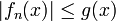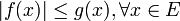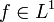puisque $f\;$ est limite simple d'une suite de fonctions mesurables, elle est mesurable et comme pour tout $n\;$ on a $|f_{n}(x)|\leq g(x)$ , par passage à la limite, $|f(x)|\leq g(x), \forall x \in E$ donc $f \in L^1$ .

Ensuite, on a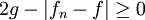 $2g - |f_{n} - f| \geq 0$ donc on peut appliquer le lemme de Fatou,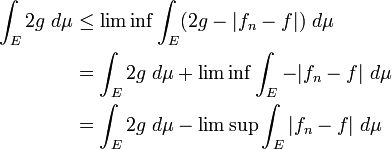

$\begin{align} \int_{E}2g \ d\mu &\leq \liminf \int_{E} (2g - |f_{n} - f|) \ d\mu\\ \ & = \int_{E} 2g \ d\mu + \liminf \int_{E} - |f_{n} - f| \ d\mu\\ \ & = \int_{E} 2g \ d\mu - \limsup \int_{E} |f_{n} - f| \ d\mu\\ \end{align}$

et comme 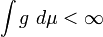$\int g \ d\mu < \infty \;$ alors,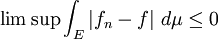 $\limsup \int_{E} |f_{n} - f|\ d\mu \leq 0$

d'où
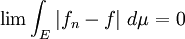
$\lim \int_{E} |f_{n} - f|\ d\mu = 0$
et donc on en déduit :

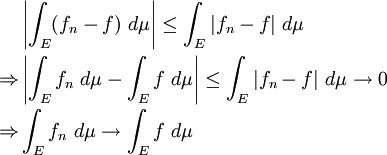
$\begin{align} \ & \left|\int_{E}(f_{n}-f)\ d\mu \right| \leq \int_{E}|f_{n}-f| \ d\mu\\ \Rightarrow & \left|\int_{E} f_{n}\ d\mu - \int_{E} f \ d\mu \right| \leq \int_{E}|f_{n}-f|\ d\mu \rightarrow 0\\ \Rightarrow & \int_{E} f_{n} \ d\mu \rightarrow \int_{E} f \ d\mu \end{align}$

$\square$

Généralisation

En théorie de la mesure on peut définir la notion de propriété presque partout, c'est pourquoi on peut énoncer le théorème de convergence dominée de façon plus générale :

Théorème — Soit 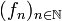$(f_{n})_{n \in \mathbb{N}}$ une suite de fonctions mesurables sur 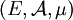$(E,\mathcal A,\mu)$ , un espace mesuré, à valeurs dans $\mathbb R$ ou $\mathbb C$ telle que :

La suite de fonctions 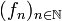$(f_{n})_{n \in \mathbb{N}}$ admet une limite presque partout , c'est-à-dire, 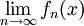$\lim_{n \to \infty} f_{n}(x)$ existe presque partout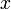 $x\;$

Il existe une fonction 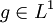$g \in L^1$ telle que :

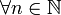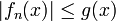$\forall n \in \mathbb N$ , $|f_{n}(x)|\leq g(x)$ $μ$ - presque partout.
Alors
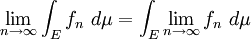
$\lim_{n \to \infty} \int_{E}{ f_{n} \ d\mu}= \int_{E} \lim_{n \to \infty} f_{n} \ d\mu$

Afin de démontrer ce théorème, il suffit de faire en sorte de se ramener au cas précédent en s'affranchissant des parties négligeables.

Démonstration

Soit 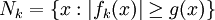$N_{k} = \{ x : |f_{k}(x)|\geq g(x) \}$ , alors 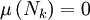$\mu\left( N_{k}\right) = 0$ pour tout 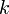$k\;$ car ces ensembles sont négligeables. En posant 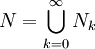$N = \bigcup_{k=0}^{\infty} N_{k}$ on a toujours 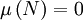$\mu\left( N \right) = 0$ et ainsi on peut redéfinir $f k = 0$ sur $N$ ce qui permet de se ramener au théorème de convergence dominée dans le cas simple.

Remarque :

Dans le cas d'une mesure de probabilité la première hypothèse peut être modifiée en :

La suite de fonctions 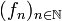$(f_{n})_{n \in \mathbb{N}}$ converge en probabilité vers une fonction mesurable $f$ .

Exemple d'application

Si 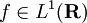$f\in L^1(\mathbf{R})$ , sa transformée de Fourier 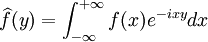$\widehat{f}(y)=\int_{-\infty}^{+\infty}f(x)e^{-ixy}dx$ est continue La vérification de l'hypothèse de domination est immédiate, puisque 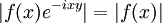$\vert f(x)e^{-ixy}\vert=\vert f(x)\vert$ ; le théorème de convergence dominée permet de voir que 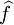$\widehat{f}\,$ est séquentiellement continue, donc continue.

Voir aussi

Théorème d'interversion série-intégrale

Théorème de convergence monotone

Portail des mathématiques

Ce document provient de « Th%C3%A9or%C3%A8me de convergence domin%C3%A9e ».

Catégories : Théorème de mathématiques | Théorie de la mesure

Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme de convergence dominee de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Théorème de convergence dominée — En mathématiques, et plus précisément en analyse, le théorème de convergence dominée est un des théorèmes principaux de la théorie de l intégration de Lebesgue. Sommaire 1 Le théorème de convergence dominée 2 Généralisation 3 Exemple d a … Wikipédia en Français
Theoreme de convergence monotone — Théorème de convergence monotone En mathématiques, le Théorème de convergence monotone est l un des théorèmes importants de la théorie des intégrales au sens de Lebesgue avec le théorème de convergence dominée. Ce théorème indique que la… … Wikipédia en Français
Théorème de convergence majorée et minorée — Théorème de convergence dominée Le théorème de convergence dominée est un des théorèmes principaux de la théorie de l intégration de Lebesgue. Sommaire 1 Le théorème de convergence dominée 2 Généralisation 3 Exemple d application … Wikipédia en Français
Théorème de convergence monotone — En mathématiques, le théorème de convergence monotone, ou théorème de Beppo Levi, est l un des théorèmes importants de la théorie des intégrales au sens de Lebesgue avec le théorème de convergence dominée, qui s en déduit. Ce théorème indique que … Wikipédia en Français
Théorème de Beppo-Levi — Théorème de convergence monotone En mathématiques, le Théorème de convergence monotone est l un des théorèmes importants de la théorie des intégrales au sens de Lebesgue avec le théorème de convergence dominée. Ce théorème indique que la… … Wikipédia en Français
Convergence Uniforme — Suite de fonctions convergeant uniformément vers la fonction valeur absolue. La convergence uniforme d une suite de fonctions est une forme de convergence plus exigeante que la convergence simple. Cette dern … Wikipédia en Français
Convergence Simple — En mathématiques, la convergence simple ou ponctuelle est une notion de convergence dans un espace fonctionnel, c’est à dire dans un ensemble de fonctions entre deux espaces topologiques. C est une définition peu exigeante : elle est plus… … Wikipédia en Français
Convergence ponctuelle — Convergence simple En mathématiques, la convergence simple ou ponctuelle est une notion de convergence dans un espace fonctionnel, c’est à dire dans un ensemble de fonctions entre deux espaces topologiques. C est une définition peu… … Wikipédia en Français
Theoreme d'Egoroff — Théorème d Egoroff Le théorème d’Egoroff, nommé ainsi en hommage à Dimitri Egoroff, un phycisien et géomètre russe, établit une condition de convergence uniforme dans certains espaces mesurables. Ce théorème peut servir en particulier à montrer… … Wikipédia en Français
Theoreme d'interversion serie-integrale — Théorème d interversion série intégrale Théorème d intégration termes à termes de la fonction somme d une série de fonctions Soit un espace vectoriel normé. Soit I un intervalle quelconque de . Soit une suite de fonctions de I dans … Wikipédia en Français

Mark and share
Search through all dictionaries
Translate…
Search Internet

Share the article and excerpts