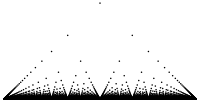
- Fonction de Thomae
-
Graphe de la fonction de Thomae sur [0,1]
En mathématiques, la fonction de Thomae est une variante de la fonction de Dirichlet. Elle a été définie en 1875 par le mathématicien Carl Johannes Thomae (de). C'est un exemple de fonction définie sur R, continue en tout point d'une partie dense mais également discontinue sur une autre partie dense.
La fonction de Dirichlet est définie sur R par :
- D(x) = 0 si x est irrationnel
- D(x) = 1 si x est rationnel
Elle est discontinue partout et n'est pas intégrable au sens de Riemann.
La fonction de Thomae est définie comme suit :
- T(x) = 0 si x est irrationnel
- T(x) = 1 si x = 0
- T(x) = 1/n si x est rationnel non nul, de la forme m/n avec m entier relatif et n entier naturel premiers entre eux.
Elle est discontinue en tout point rationnel, continue en tout point irrationnel, réglée (c'est-à-dire limite uniforme d'une suite de fonctions en escalier Tn) et intégrable au sens de Riemann. Chaque Tn peut même être choisie nulle sauf en un nombre fini de points donc d'intégrale nulle, si bien que
.Référence
(en) K. Beanland, J. W. Roberts et C. Stevenson, Modifications of Thomae's function and differentiability, Amer. Math. Monthly, 116, n°6 (juin-juillet 2009), 531-535 [lire en ligne]
Lien externe
(en) Eric W. Weisstein, « Dirichlet Function », MathWorld
Catégories :- Analyse réelle
- Fonction remarquable
Wikimedia Foundation. 2010.
