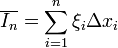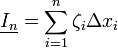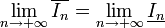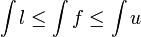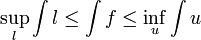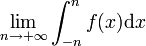- Integrale de Riemann
-
Intégrale de Riemann
En analyse réelle, l'intégrale de Riemann est une façon simple de définir l'intégrale d'une fonction sur un intervalle. En termes géométriques, cette intégrale s'interprète comme l'aire du domaine sous la courbe représentative de la fonction, comptée algébriquement.
Le procédé général utilisé pour définir l'intégrale de Riemann est l'approximation par des fonctions en escalier, pour lesquelles la définition de l'aire sous la courbe est aisée. Les fonctions pour lesquelles cette définition est possible sont dites intégrables au sens de Riemann. C'est le cas notamment des fonctions continues, continues par morceaux, ou réglées sur un segment [a,b].
On obtient un procédé d'intégration plus général et plus satisfaisant, notamment vis-à-vis du passage à la limite, en introduisant l'intégrale de Lebesgue ou l'intégrale de Kurzweil-Henstock.
Sommaire
Définition de l'intégrale
Les fonctions en escalier
Article détaillé : fonction en escalier.Soit E un sous-ensemble quelconque du segment [a,b]. Soit χE la fonction qui vaut 1 si x appartient à E et 0 sinon. χE est appelée la fonction indicatrice ou fonction caractéristique de E.
Ces fonctions sont notre point de départ et nous posons :
pour tout segment [c,d] inclus dans [a,b] et pour toute constante
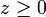 ,
,![\int z \chi_{[c,d]}(x)\,\mathrm d x = z(d-c)](/pictures/frwiki/52/4b651bc2e76c289da1af97e63d7107b5.png) .
.
Dans ce cas l'aire sous la courbe de cette fonction est égale à l'aire du rectangle de base [c,d] et de hauteur z. De la même manière, quelques expérimentations géométriques avec de telles fonctions nous amènent à penser que si f1,f2,...,fn sont n fonctions indicatrices sur des intervalles disjoints et si a1,a2,...,an sont des scalaires positifs, alors l'aire du domaine sous la courbe de la fonction
doit être égale à
Une fonction de cette forme est appelée une combinaison linéaire de fonction indicatrices, ou tout simplement une fonction en escalier. Remarquons maintenant que nous avons décidé quelle devrait être l'intégrale d'une fonction en escalier. Nous prenons un raccourci maintenant en déclarant que la formule précédente reste valable si certains coefficients aj sont négatifs. Une différence cruciale entre l'intégrale de Riemann et celle de Lebesgue, est que les fonctions en escalier de l'intégrale de Lebesgue sont des combinaisons linéaires de fonctions indicatrices sur des ensembles qui ne sont pas nécessairement des intervalles. Bien sûr, nous devons travailler davantage pour pouvoir calculer des intégrales d'une plus grande classe de fonctions que celle des fonctions en escalier. Aussi remarquons que l'intégrale de Lebesgue n'utilise pas de sommes supérieures, et que les fonctions positives sont traitées en premier, avant d'étendre l'intégrale aux fonctions qui peuvent prendre des valeurs négatives.
Définition générale
Soit f continue sur [a,b]. Soit x0,x1,...,xn une subdivision ordonnée de [a,b] (avec x0 = a et xn = b), on note Δxi = xi − xi − 1 et on a
 .
.Alors pour toute fonction f on pose :
et on note
Alors, on dit que f est intégrable au sens de Riemann sur [a,b] si pour toute subdivision ordonnée, on observe que :
On note alors l'intégrale de f sur [a,b] par
Fonctions à valeurs réelles : intégrales inférieure et supérieure
À partir d'observations géométriques, simplement en voyant que le domaine Sf[réf. nécessaire] est un sous-ensemble de Sg[réf. nécessaire] (Au moins dans le cas de fonctions positives, ceci est clair.), nous imposons que si f vérifie pour tout x de [a,b],
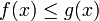 alors
alorsNous appelons cette propriété la croissance de l'intégrale.
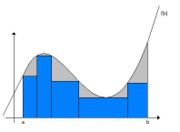
L'intégrale d'une fonction en escalier étant définie et la condition de monotonie étant imposée, nous pouvons intégrer des fonctions à valeurs positives arbitraires. Soit f une fonction à valeurs réelles définie sur [a,b] et soit l une fonction en escalier telle que pour tout x on ait,
 . De plus, soit u une fonction en escalier telle que pour tout x on ait,
. De plus, soit u une fonction en escalier telle que pour tout x on ait, 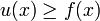 . Si nous devions donner une valeur à
. Si nous devions donner une valeur à 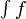 conforme à la condition de monotonie, alors nous devrions avoir :
conforme à la condition de monotonie, alors nous devrions avoir :L'intégrale
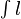 est alors appelée une somme inférieure pour f et l'intégrale
est alors appelée une somme inférieure pour f et l'intégrale 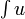 est alors appelée une somme supérieure pour f. L'inégalité précédente doit être vérifiée pour toutes sommes supérieures et inférieures de f, donc nous pouvons en déduire une autre inégalité :
est alors appelée une somme supérieure pour f. L'inégalité précédente doit être vérifiée pour toutes sommes supérieures et inférieures de f, donc nous pouvons en déduire une autre inégalité :où
 est la borne supérieure de toutes les sommes inférieures, et
est la borne supérieure de toutes les sommes inférieures, et 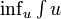 est la borne inférieure de toutes les sommes supérieures. Le nombre
est la borne inférieure de toutes les sommes supérieures. Le nombre  est parfois appelé intégrale inférieure de f ; de la même manière, le nombre
est parfois appelé intégrale inférieure de f ; de la même manière, le nombre 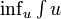 est appelé intégrale supérieure.
est appelé intégrale supérieure.Si les intégrales supérieures et inférieures sont égales, alors il y a seulement une façon de définir
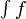 . Il ne peut pas arriver que l'intégrale inférieure soit plus grande que l'intégrale supérieure (par construction, comme le lecteur peut le vérifier). Cependant, il peut arriver que l'intégrale supérieure ne soit pas égale à l'intégrale inférieure. Par exemple, le lecteur peut vérifier cela, pour la fonction indicatrice χQ où Q est l'ensemble des nombres rationnels du segment [a,b] avec a < b, l'intégrale inférieure est égale à 0 et l'intégrale supérieure est égale à b − a > 0.
. Il ne peut pas arriver que l'intégrale inférieure soit plus grande que l'intégrale supérieure (par construction, comme le lecteur peut le vérifier). Cependant, il peut arriver que l'intégrale supérieure ne soit pas égale à l'intégrale inférieure. Par exemple, le lecteur peut vérifier cela, pour la fonction indicatrice χQ où Q est l'ensemble des nombres rationnels du segment [a,b] avec a < b, l'intégrale inférieure est égale à 0 et l'intégrale supérieure est égale à b − a > 0.Toutes les fonctions dont les intégrales inférieures et supérieures sont finies et égales, constituent l'ensemble des fonctions intégrables au sens de Riemann ou Riemann-intégrables. En revanche, les fonctions qui ont des intégrales inférieures et supérieures différentes sont dites non intégrables au sens de Riemann. Dans le contexte de cet article, nous dirons intégrable ou non intégrable sachant que nous parlons d'« intégrabilité » au sens de Riemann.
On peut vérifier qu'une fonction en escalier a une intégrale égale à ses intégrales supérieures et inférieures.
Propriétés
Lemme 1 — Soit [a,b] un segment. L'application
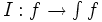 qui associe à f l'intégrale de a à b est une forme linéaire. Et ainsi pour toutes fonctions intégrables f et g, et tout nombre réel λ, I(λf + g) = λI(f) + I(g).
qui associe à f l'intégrale de a à b est une forme linéaire. Et ainsi pour toutes fonctions intégrables f et g, et tout nombre réel λ, I(λf + g) = λI(f) + I(g).Ceci peut être démontré à partir des premiers principes de la construction de l'intégrale de Riemann.
Théorème 2 — Toute fonction à valeurs réelles, continue sur le segment [a,b] est intégrable.
La preuve repose sur le fait qu'une fonction continue sur un segment est uniformément continue.
Corollaire 3 — Si f est continue sur [a,b] sauf peut-être en un nombre fini de points de discontinuité, et si f est bornée, alors f est intégrable.
La condition f bornée ne peut pas être omise.
Théorème 4 — Si (fk) est une suite de fonctions intégrables sur [a,b], et si (fk) converge uniformément vers une fonction f, alors f est intégrable, et les intégrales
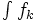 convergent vers
convergent vers 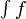 .
.Corollaire 5 — Soit C(a,b) l'espace de Banach des fonctions continues sur [a,b] muni de la norme de convergence uniforme. Alors
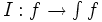 est continue. Conjointement avec le lemme 1, nous pouvons en déduire que l'intégrale est une forme continue sur C(a,b).
est continue. Conjointement avec le lemme 1, nous pouvons en déduire que l'intégrale est une forme continue sur C(a,b).Les hypothèses du théorème 4 (convergence uniforme sur un segment) sont très fortes. Une première difficulté avec l'intégrale de Riemann se pose, lorsque nous tentons d'amoindrir ces hypothèses. En fait, la suite numérique
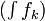 converge vers le nombre
converge vers le nombre 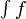 plus souvent que le théorème le suggère, mais il est très difficile de le prouver dans cet ensemble. La meilleure façon d'avoir un théorème plus fort est d'utiliser l'intégrale de Lebesgue.
plus souvent que le théorème le suggère, mais il est très difficile de le prouver dans cet ensemble. La meilleure façon d'avoir un théorème plus fort est d'utiliser l'intégrale de Lebesgue.Un autre problème avec l'intégrale de Riemann est qu'elle ne s'étend pas aux intervalles non bornés très facilement. Si nous souhaitons intégrer une fonction f de
 à
à 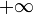 , nous pouvons calculer
, nous pouvons calculerCependant, certaines propriétés (telles que l'invariance par translation, le fait que l'intégrale de Riemann ne change pas si nous translatons l'intégrande f) ne sont plus vérifiées. En fait, le Théorème 4 devient faux pour une telle intégrale, et il devient très difficile d'utiliser des limites conjointement avec l'intégrale. De telles intégrales sont appelées intégrales impropres. À nouveau, l'intégration de Lebesgue allège ces difficultés.
Sommes de Riemann
Article détaillé : somme de Riemann.Les sommes de Riemann sont une méthode d'approximation des intégrales. Elles peuvent être utilisées pour définir la notion d'intégrale.
Comparaison avec d'autres procédés d'intégration
- Portail des mathématiques
Catégories : Théorie de l'intégration | Analyse réelle | Bernhard Riemann
Wikimedia Foundation. 2010.


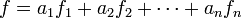
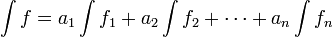
![\xi_i= \sup_{x\in [x_{i-1} ,x_i]} f(x)](/pictures/frwiki/99/cb02dc010d0829a4af2ce239fcb065f9.png)
![\zeta_i= \inf_{x\in [x_{i-1} ,x_i]} f(x)](/pictures/frwiki/54/69ac222de2d3e30dac84408f53841c34.png)