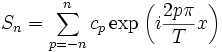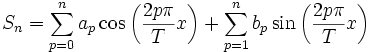Serie trigonometrique

Serie trigonometrique

Série trigonométrique

Une série trigonométrique est une suite particulière de polynômes trigonométriques. La série possède une fréquence fondamentale f, et on somme successivement des fonctions trigonométriques de fréquence n.f pour des valeurs entières de n.

Le terme d'ordre n de la série a donc la forme suivante

S_n = \sum_{p=-n}^n c_p \exp \left(i \frac{2p\pi}{T} x\right)~

si on travaille avec des notations complexes. Mais on utilise aussi couramment

S_n = \sum_{p=0}^n a_p \cos \left( \frac{2p\pi}{T} x\right)+ \sum_{p=1}^n b_p \sin \left( \frac{2p\pi}{T} x\right)~

si on a une série trigonométrique à valeurs réelles

L'exemple le plus classique de série trigonométrique est la série de Fourier associée à une fonction périodique intégrable.

Sommaire

Théorème d'unicité de Cantor

On doit à Georg Cantor le théorème d'unicité pour les séries trigonométriques, prouvé en 1870.

Théorème : si une série trigonométrique converge en tout point vers la fonction nulle, alors tous ses coefficients sont nuls. Ainsi deux séries trigonométriques qui ont la même limite simple ont les mêmes coefficients.

Cantor a lui-même étendu son résultat, le rendant valable lorsqu'il y a convergence en tout point sauf un nombre fini. (C'est d'ailleurs en cherchant à généraliser ce résultat que Cantor sera amené à introduire la notion de nombre ordinal).

D'autres extensions ont suivi. On appelle ensemble d'unicité un sous-ensemble de la droite réelle, défini modulo 2π, sur lequel le résultat d'unicité de Cantor s'étend.

  • en 1909, Young démontre que les ensembles dénombrables sont des ensembles d'unicité
  • on sait depuis leur définition par Lebesgue que les ensembles dont la mesure de Lebesgue est positive n'en sont pas
  • en 1916, Menchoff donne un exemple d'ensemble de mesure nulle qui n'est pas un ensemble d'unicité[1]
  • de nombreux résultats plus précis se sont ajoutés depuis

Lien avec les séries de Fourier

Selon un théorème de Lebesgue de 1902, si une série trigonométrique converge simplement vers une fonction bornée, alors c'est la série de Fourier de cette fonction. Comme le résultat de Menchoff signalé ci-dessus l'illustre, ce théorème serait en défaut si on remplaçait la convergence simple par une convergence presque partout.

Ces théorèmes d'unicité ne doivent pas être confondus avec le théorème d'injectivité des coefficients de Fourier : deux fonctions intégrables, périodiques, ont les mêmes coefficients de Fourier. Voir l'article série de Fourier.

Le problème de l'existence d'une décomposition

Si f est une fonction mesurable, finie presque partout, un théorème de Menchoff montre qu'il existe une série trigonométrique qui converge vers f presque partout[2].

Notes et références

  1. ↑ Dmitry Menchoff, Sur l'unicité du développement trigonométrique, C.R. Acad. Sci. Paris 163 (1916), p. 433-436
  2. ↑ Dmitry Menchoff, Sur la représentation des fonctions mesurables par des séries trigonométriques, Mat. Sb. 9 51 (1941), p 667-692

Bibliographie

  • Jean-Pierre Kahane, Pierre-Gilles Lemarié-Rieusset, Séries de Fourier et ondelettes [détail des éditions]
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « S%C3%A9rie trigonom%C3%A9trique ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Serie trigonometrique de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Série trigonométrique — Une série trigonométrique est une suite particulière de polynômes trigonométriques. La série possède une fréquence fondamentale f, et on somme successivement des fonctions trigonométriques de fréquence n.f pour des valeurs entières de n. Le terme …   Wikipédia en Français

  • Serie de Fourier — Série de Fourier Le premier graphe donne l allure du graphe d une fonction périodique ; l histogramme donne les valeurs des modules des coefficients de Fourier correspondant aux différentes fréquences. En analyse, les séries de Fourier sont… …   Wikipédia en Français

  • Série de fourier — Le premier graphe donne l allure du graphe d une fonction périodique ; l histogramme donne les valeurs des modules des coefficients de Fourier correspondant aux différentes fréquences. En analyse, les séries de Fourier sont un outil… …   Wikipédia en Français

  • Série numérique — Série (mathématiques) Pour les articles homonymes, voir Série. En mathématiques, la série constitue une généralisation de la notion de somme, pour une succession infinie de termes. L étude des séries consiste à effectuer la somme d un nombre fini …   Wikipédia en Français

  • Série semi-convergente — Série (mathématiques) Pour les articles homonymes, voir Série. En mathématiques, la série constitue une généralisation de la notion de somme, pour une succession infinie de termes. L étude des séries consiste à effectuer la somme d un nombre fini …   Wikipédia en Français

  • Série de Fourier — En analyse, les séries de Fourier sont un outil fondamental dans l étude des fonctions périodiques. C est à partir de ce concept que s est développée la branche des mathématiques connue sous le nom d analyse harmonique. L étude d une fonction… …   Wikipédia en Français

  • Série (mathématiques) — Pour les articles homonymes, voir Série. En mathématiques, la série constitue une généralisation de la notion de somme pour une succession infinie de termes. L étude des séries consiste à évaluer la somme d un nombre fini n de termes successifs,… …   Wikipédia en Français

  • trigonométrique — [ trigɔnɔmetrik ] adj. • 1718; de trigonométrie ♦ Sc. Qui concerne la trigonométrie; qui est utilisé en trigonométrie. Lignes trigonométriques : les fonctions circulaires définies par leur projection sur un axe. Calculs, tables trigonométriques.… …   Encyclopédie Universelle

  • Serie de Laurent — Série de Laurent Karl Weierstrass. Cet article traite du développement en série de Laurent en analyse complexe. Pour la définition et les propriétés des séries de Laurent formelles en algèbre, veuillez consulter l article Série de Laurent… …   Wikipédia en Français

  • Série de laurent — Karl Weierstrass. Cet article traite du développement en série de Laurent en analyse complexe. Pour la définition et les propriétés des séries de Laurent formelles en algèbre, veuillez consulter l article Série de Laurent formelle. En analyse… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”