Intégrale de Riemann-Stieltjes

Intégrale de Riemann-Stieltjes

Intégrale de Stieltjes

Thomas Stieltjes (1856–1894)

L'intégrale de Stieltjes constitue une généralisation de l'intégrale ordinaire, ou intégrale de Riemann. En effet, considérons deux fonctions réelles bornées f et g définies sur un intervalle fermé [a,b], ainsi qu'une subdivision a = x0 < x1 < x2 < ... < xn − 1 < xn = b de cet intervalle. Si la somme de Riemann

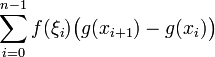\sum_{i=0}^{n-1}f(\xi_i )\bigl(g(x_{i+1})-g(x_i)\bigr),

avec ξi ∈ [xi, xi+1], tend vers un nombre fixe S lorsque max(xi+1 – xi) tend vers 0, alors S est appelé l'intégrale de Stieltjes (ou parfois l'intégrale de Riemann-Stieltjes) de la fonction f par rapport à g, et on la dénote par

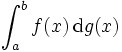
\int_a^bf(x)\,\mathrm{d}g(x)

ou, simplement, par

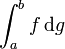\int_a^b f\,\mathrm{d}g.

Si les fonctions f et g possèdent un point de discontinuité en commun, alors l'intégrale n'existe pas. Cependant, si f est continue et g' = dg / dx possède une intégrale de Riemann sur l'intervalle considéré, alors

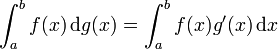\int_a^bf(x)\,\mathrm{d}g(x)=\int_a^bf(x)g'(x)\,\mathrm{d}x.

Plus généralement, si f est continue et g à variations bornées, cette intégrale est bien définie.

Voir aussi

Œuvres

  • Recherches sur les fractions continues, Annales de la Faculté des Sciences de Toulouse, 8, No. 4, J1–J122, 1894.

Bibliographie

  • (en) H. Jeffreys & B.S. Jeffreys (1988). Integration: Riemann, Stieltjes, §1.10 Methods of Mathematical Physics, 3rd ed., Cambridge University Press, Cambridge, pp. 26–36. (ISBN 0-52166402-0).
  • (en) H. Kestelman (1960). Riemann-Stieltjes Integration, Modern Theories of Integration, Dover Publications, New York. Chap. 11, pp. 247–269.
  • Portail des mathématiques Portail des mathématiques
  • Portail de la géodésie et de la géophysique Portail de la géodésie et de la géophysique
  • Portail de la physique Portail de la physique
Ce document provient de « Int%C3%A9grale de Stieltjes ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Intégrale de Riemann-Stieltjes de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Intégrale de Riemann — Interprétation géométrique de l intégrale de la fonction f. En analyse réelle, l intégrale de Riemann[1] est une façon simple de définir l intégrale d une fonction sur un …   Wikipédia en Français

  • Integrale de Stieltjes — Intégrale de Stieltjes Thomas Stieltjes (1856–1894) L intégrale de Stieltjes constitue une généralisation de l intégrale ordinaire, ou intégrale de Riemann. En effet, considérons deux fonctions réelles bornées f …   Wikipédia en Français

  • Intégrale De Stieltjes — Thomas Stieltjes (1856–1894) L intégrale de Stieltjes constitue une généralisation de l intégrale ordinaire, ou intégrale de Riemann. En effet, considérons deux fonctions réelles bornées f …   Wikipédia en Français

  • Intégrale de stieltjes — Thomas Stieltjes (1856–1894) L intégrale de Stieltjes constitue une généralisation de l intégrale ordinaire, ou intégrale de Riemann. En effet, considérons deux fonctions réelles bornées f …   Wikipédia en Français

  • Intégrale de Stieltjes — Thomas Stieltjes (1856–1894) L intégrale de Stieltjes constitue une généralisation de l intégrale ordinaire, ou intégrale de Riemann. En effet, considérons deux fonctions réelles bornées f et …   Wikipédia en Français

  • Intégrale de Daniell — En mathématiques, l intégrale de Daniell est un type d intégration qui généralise le concept plus élémentaire de l intégrale de Riemann qui est généralement la première enseignée. Une des principales difficultés de la formulation traditionnelle… …   Wikipédia en Français

  • STIELTJES (T.-J.) — STIELTJES THOMAS JEAN (1856 1894) Mathématicien se sentant une profonde vocation pour les travaux théoriques, Thomas Stieltjes fit le tour de toute l’analyse de son époque. Sa méthode de recherche s’apparentait à celle de Gauss: découvrir les… …   Encyclopédie Universelle

  • Integrale d'Ito — Intégrale d Itō L intégrale d Itō, appelée ainsi en l honneur du mathématicien Kiyoshi Itō est un des outils fondamentaux du calcul stochastique. Il s agit d une intégrale définie de façon similaire à l intégrale de Riemann comme limite d une… …   Wikipédia en Français

  • Intégrale d'Itô — Intégrale d Itō L intégrale d Itō, appelée ainsi en l honneur du mathématicien Kiyoshi Itō est un des outils fondamentaux du calcul stochastique. Il s agit d une intégrale définie de façon similaire à l intégrale de Riemann comme limite d une… …   Wikipédia en Français

  • Intégrale de Lebesgue — En mathématiques, l’intégrale de Lebesgue désigne à la fois une théorie relative à l intégration et à la mesure, puis le résultat de l intégration d une fonction à valeurs réelles définie sur (ou sur ), munis de la mesure de Lebesgue.… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”