Groupe Topologique Compact

Un groupe topologique compact ou groupe compact est un groupe topologique G tel que l'espace topologique sous-jacent soit compact. Les groupes compacts sont des groupes unimodulaires, dont la compacité simplifie l'étude. Ces groupes comprennent notamment les groupes finis, et les groupes de Lie compact. Tout groupe topologique compact est limite projective de groupes de Lie compacts.

Sommaire 1 Exemples de groupes compacts 1.1 Groupe fini 1.2 Construction de groupes compacts 1.3 Groupe de Lie compact 2 Intégration sur les groupes compacts 2.1 Unimodulaire 2.2 Théorème du point fixe de Kakutani 3 Représentation des groupes compacts 3.1 Complète réductibilité 3.2 Théorème de Peter-Weyl 3.3 Caractère 3.4 Représentation des groupes finis

Exemples de groupes compacts

Groupe fini

Tout groupe fini, muni de la topologie discrète, est un groupe topologique compact. En effet :

• Tout ensemble fini muni de la topologie discrète est séparé et admet un nombre fini d'ouverts ; il est donc compact.
• Toute application entre espaces munis de la topologie discrète est continue ; la multiplication et l'inversion sont donc automatiquement continues.

L'étude proprement dite des groupes finis ne fait pas appel aux notions topologiques. Toutefois :

• Des propriétés concernant les groupes compacts sont toujours vérifiées pour les groupes finis.
• Les sous-groupes discrets d'un groupe compact sont des groupes finis.

Construction de groupes compacts

Des groupes compacts peuvent se construire en utilisant les méthodes générales de construction des groupes topologiques :

• Le produit direct de groupes compacts est un groupe compact.
• Un sous-groupe fermé d'un groupe compact est un groupe compact.
• Le quotient d'un groupe compact par un sous-groupe normal fermé est un groupe compact.
• Le noyau d'un morphisme continu propre entre groupes topologiques 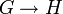est un sous-groupe compact de G.
• La limite projective d'une famille de groupes topologiques compacts est un groupe compact. En particulier, les groupes profinis sont des exemples de groupes compacts.

Groupe de Lie compact

Un groupe de Lie compact est un groupe de Lie (réel ou complexe) dont l'espace topologique sous-jacent est compact. Parmi eux, on peut citer les groupes de Lie classique compacts ; dont voici la liste :

• Le groupe orthogonal 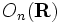, de dimension n(n − 1) / 2 ;
• Le groupe spécial orthogonal 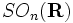, qui en est sa composante neutre ;
• Le groupe unitaire 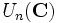, de dimension n² ;
• Le groupe spécial unitaire 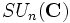, de dimension n² − 1 ;
• Le groupe compact symplectique SP(n), de dimension n(2n + 1).

Il est à remarquer qu'un groupe de Lie compact complexe est nécessairement commutatif.

Intégration sur les groupes compacts

Sur tout groupe topologique localement compact et séparable G, il existe une mesure borélienne invariante par les translations à gauche, appelée mesure de Haar, unique à coefficient multiplicatif près. Elle est finie sur les parties compactes de G. Si G est lui-même compact, toute mesure de Haar est finie, et il est possible de la normaliser pour que sa masse vaille 1. On dispose ainsi sur tout groupe topologique compact G d'une unique mesure de probabilité qui soit invariante par translations à gauche, qu'on nomme par abus de langage la mesure de Haar de G, notée λ dans la suite de l'article.

En pratique, la mesure de Haar permet de moyenner les objets sur G pour obtenir des objets invariants.

Unimodulaire

Un groupe topologique localement compact et séparable est dit unimodulaire si une (et donc toute) mesure de Haar est invariante à droite. Tout groupe topologique compact est unimodulaire.

En général, le translaté à droite d'une mesure de Haar λ par g est une mesure de Haar, donc s'écrit Δ(g).λ. Le coefficient réel Δ(g) est indépendant du choix de λ et 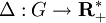est un morphisme continu de groupes topologiques. Si G est compact, l'image de Δ est un sous-groupe compact de  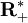: a fortiori, il est trivial. L'application Δ est dans ce cas constante égale à 1. Toute mesure de Haar est invariante par les translations à droite.

Théorème du point fixe de Kakutani

Le théorème suivant a été démontré par Shizuo Kakutani en 1941 :

• Théorème du point fixe de Kakutani : Soient V un espace vectoriel topologique localement convexe séparé, G un groupe topologique compact, et 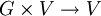une action linéaire continue de G sur V. Supposons donnée une partie C convexe compacte non vide de V globalement stable par l'action de G. Alors il existe un point c dans C fixe par tous les éléments g de G (g.c=c).

Le théorème de Kakutani donne une preuve élémentaire de l'existence de la mesure de Haar sur un groupe compact G. En effet, l'espace des mesures réelles finies 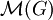est par le théorème de Riesz le dual topologique de l'espace de Banach des fonctions continues réelles 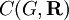, muni de la norme de convergence uniforme. Les mesures boréliennes de probabilité forment un sous-ensemble convexe et *-faiblement compact. L'action de G sur lui-même par translations à gauche induit une action linéaire de G sur 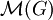, qui soit continue pour la topologie *-faible. Le convexe C est stable par G : de fait, le théorème de Kakutani s'applique et donne l'existence d'un point fixe de l'action de G dans C, autrement dit d'une mesure borélienne de probabilité sur G invariante par translation à gauche. L'existence de la mesure de Haar se trouve ainsi établie. (Cependant, la compacité ne permet pas de simplifier la preuve de l'unicité.)

Représentation des groupes compacts

Complète réductibilité

Une représentation d'un groupe topologique G est une action continue linéaire de G sur un espace vectoriel topologique réel ou complexe V. La représentation est dite de dimension finie si V est de dimension finie : dans ce cas, la représentation peut être définie par un morphisme continu 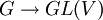. Elle est dite unitaire si V est un espace euclidien ou hermitien et si ρ est à valeurs dans le groupe orthogonal O(V) ou unitaire U(V).

• Toute [représentation réelle ou complexe de dimension finie d'un groupe topologique compact G est équivalente à une représentation unitaire.

En effet, soit E un espace vectoriel réel ou complexe de dimension finie et 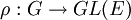un morphisme continu. Prenons < . | . > une structure euclidienne ou hermitienne quelconque sur E. Posons pour tous vecteurs v et w :

(v | w) =	∫	< g − 1.v | g − 1.w > dλ(g)
	G

.

On constate que (. | .) définit une forme sesquilinéaire sur E et définie positive (donc une structure euclidienne ou hermitienne). Vérifions qu'elle est invariante sous l'action de G. Pour h dans G, et v et w dans E, il vient :

(h.v | h.w) =	∫	< g − 1h.v | g − 1h.w > dλ(g) =	∫	< (h − 1g) − 1.v | (h − 1g) − 1.w > dλ(g) =	∫	< g − 1.v | g − 1.w > dλ(g) = (v | w)
	G		G		G

.

La dernière égalité provient de l'invariance à gauche de la mesure de Haar λ.

Une représentation d'un groupe topologique G dans un espace V est dite irréductible s'il n'existe aucun sous-espace vectoriel fermé dans V globalement invariant par l'action linéaire de G. Elle est dite complètement réductible si l'espace V est la somme directe d'une famille de sous-espaces fermés invariants, dont la représentation induite sur chacun est irréductible.

• Toute représentation d'un groupe compact de dimension finie est complètement réductible.

Toute représentation unitaire de dimension finie est complètement réductible (lire représentation unitaire d'un groupe topologique). Or, toute représentation de dimension finie équivalente à une représentation complètement réductible est elle-même complètement réductible. D'où le résultat en appliquant la propriété précédente.

Théorème de Peter-Weyl

Le théorème de Peter-Weyl a été démontré par Hermann Weyl (1885-1955). La collection des représentations irréductibles de dimension finie à équivalence près d'un groupe topologique compact G donné forment un ensemble. Une fois fixé une mesure de Haar sur G, on dispose d'une représentation naturelle du groupe 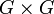dans l'algèbre hilbertienne L²(G) donnée par :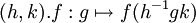

Cette représentation est unitaire. Le théorème de Peter-Weyl affirme que cette représentation est équivalente à la somme orthogonale des produits tensoriels des représentations unitaires A de G par leurs représentations duales A^*, où les représentations unitaires sont identifiées à équivalence près.

Ce théorème a des conséquences non triviales. Il permet par exemple de démontrer que tout groupe topologique compact est limite d'un système projectif de groupes de Lie compacts.

Caractère

Étant donnée une représentation complexe de dimension finie d'un groupe topologique compact G, le caractère associé est défini par :

χ_ρ(g) = Tr(ρ(g))

Les caractères de deux représentations équivalentes sont égaux. On parle de caractère et de caractère irréductible pour désigner les caractères respectivement associés à une représentation complexe et à une représentation complexe irréductible.

Une fonction centrale est une fonction (mesurable, continue, ...) 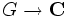constante sur les classes de conjugaison de G. Les caractères sont des exemples de fonctions centrales. La collection de tous les caractères irréductibles d'un groupe topologique compact forme une famille orthonormée de L²(G,λ). Plus exactement, c'est une base hilbertienne du sous-espace de Hilbert des fonctions centrales de classe L².

Un exemple important est la détermination des caractères du tore et la classification de ses représentations.

Représentation des groupes finis

Les propriétés des représentations des groupes compacts se spécialisent pour les groupes finis. L'étude est simplifiée, notamment parce que le nombre de caractères est fini. En particulier, les caractères irréductibles d'un groupe fini G forment une base de l'espace vectoriel de dimension finie des fonctions centrales. La dimension de cet espace est donc le nombre de classes de conjugaison de G.

• Portail des mathématiques