Fonction Centrale

Fonction centrale

En théorie des groupes, une fonction centrale est une application réelle ou complexe définie sur un groupe G et constante le long des classes de conjugaison de G. Les fonctions centrales interviennent dans l'étude des représentations d'un groupe topologique compact ; les fonctions centrales continues apparaissent comme les éléments du centre de son algèbre hilbertienne, d'où leur nom.

Définition

Étant donné un groupe G, une fonction 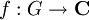$f:G\rightarrow \mathbf{C}$ est dite centrale si, pour tous s et t dans G, on a :

f (s t s - 1) = f (t)

Le groupe G agit naturellement à droite sur l'espace 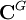$\mathbf{C}^G$ des fonctions complexes sur G par : 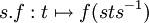$s.f:t\mapsto f(sts^{-1})$ . Les fonctions centrales sont donc les points fixes de cette action à droite.

Un exemple simple de fonctions centrales est celui des homomorphismes de groupes. Cependant, ce sont loin d'être les seules en général. Par exemple, l'application qui à un élément de G associe son ordre est une fonction centrale : l'ordre de $s t s - 1$ est le même que celui de $t$ . Cependant, sauf bien sûr pour le groupe trivial, cette application n'est jamais un homomorphisme : l'ordre d'un élément différent de l'élément neutre est toujours un entier strictement positif.

Si le groupe est muni d'une topologie rendant continus le produit et l'inversion, autrement dit, si G est un groupe topologique, on demande en général à ce qu'une fonction centrale soit mesurable ou continue.

Sur un groupe commutatif, toute fonction est une fonction centrale.

L'ensemble des fonctions centrales sur un groupe G forment un espace vectoriel complexe. Lorsque le groupe G est fini, la dimension de cet espace est le nombre de classes de conjugaison de G. Une base est donnée par la famille des fonctions indicatrices des classes de conjugaison de G.

Algèbre hilbertienne d'un groupe compact

Article détaillé : Algèbre hilbertienne d'un groupe topologique compact.

Si G est un groupe topologique compact, on note $λ$ sa mesure de Haar définie comme l'unique mesure de probabilité invariante par translation à gauche, et $L 2 (G)$ l'espace de Banach des fonctions complexes mesurables sur G et de carré intégrable contre $λ$ . Cet espace peut être muni :

D'un produit associatif et distributif d'élément neutre la fonction constante égale à 1, le produit de convolution, défini par :

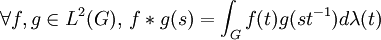
$\forall f,g\in L^2(G), \, f*g(s)=\int_Gf(t)g(st^{-1})d\lambda(t)$

D'une involution définie par :

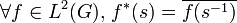
$\forall f\in L^2(G),\, f^*(s)=\overline{f(s^{-1})}$

Munis de ces lois, $L 2 (G)$ est une algèbre de Banach involutive séparable, et même une algèbre hilbertienne. L'étude de cette algèbre est liée à l'étude des représentations (lire Théorème de Peter-Weyl).

Cette relation transparait dans l'étude du centre de $L 2 (G)$ . En effet, un calcul direct donne pour toutes fonctions mesurables f et g de carré intégrable:

$f*g(s)-g*f(s)=\int_Gg(t^{-1}).\left[f(st)-f(ts)\right].d\lambda(t)$

Une fonction f appartient au centre de $L 2 (G)$ , ssi, pour toute fonction 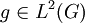$g\in L^2(G)$ , les convoluées $f * g$ et $g * f$ sont égales presque partout, donc partout car elles sont continues. De fait, cela équivaut à ce que pour presque tous s et t dans G, on a:

f (s t) = f (t s)

Le centre de $L 2 (G)$ est le sous-espace vectoriel fermé des (classes de) fonctions centrales mesurables sur G et de carré intégrable.

Caractère d'un groupe compact

Article détaillé : Caractère d'un groupe topologique compact.

Une représentation irréductible de dimension finie du groupe compact G est une application continue 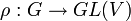$\rho:G\rightarrow GL(V)$ où V est un espace vectoriel complexe de dimension finie. Le caractère associé est la fonction centrale définie par :

$\chi_{\rho}(s)=Tr\left[\rho(s)\right]$

On appelle caractère irréductible un caractère associé à une représentation irréductible. Les caractères irréductibles sont des fonctions centrales mesurables de carré intégrable contre la mesure de Haar $λ$ . Elles permettent de caractériser l'équivalence des représentations irréductibles :

Deux représentations irréductibles équivalentes définissent le même caractère.
Les caractères associés à deux représentations non équivalentes sont orthogonaux.

La collection des caractères irréductibles forme une famille orthonormée de $L 2 (G)$ ; en fait, c'en est une base hilbertienne. Par conséquent, il y au plus un nombre dénombrable de caractères irréductibles, et donc de classes d'équivalences de représentations irréductibles de G.

Pour un groupe fini G, le nombre de représentations irréductibles est le nombre des classes de conjugaison de G.

Portail des mathématiques

Ce document provient de « Fonction centrale ».

Catégorie : Théorie des représentations

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonction Centrale de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Fonction centrale — En théorie des groupes, une fonction centrale est une application définie sur un groupe et constante le long de ses classes de conjugaison. Les fonctions centrales à valeurs complexes interviennent dans l étude des représentations d un groupe… … Wikipédia en Français
Fonction Centrale D'un Groupe Fini — En mathématiques et plus précisément en théorie des groupes une fonction centrale est une fonction définie sur un groupe et constante sur chaque classe de conjugaison. Les fonctions centrales possèdent un rôle particulier dans le cadre de la… … Wikipédia en Français
Fonction centrale d'un groupe fini — En mathématiques et plus précisément en théorie des groupes une fonction centrale est une fonction définie sur un groupe et constante sur chaque classe de conjugaison. Les fonctions centrales possèdent un rôle particulier dans le cadre de la… … Wikipédia en Français
Fonction centrale sur un groupe fini — En mathématiques, et plus précisément en théorie des groupes, une fonction centrale sur un groupe fini est un exemple de fonction centrale sur un groupe : c est une application définie sur un groupe fini et centrale, c est à dire constante… … Wikipédia en Français
Centrale nucléaire de Tihange — Tours de refroidissement de la centrale nucléaire de Tihange, vue de la Meuse Administration Pays … Wikipédia en Français
Centrale nucléaire de Doel — Centrale nucléaire de Doel, sur l estuaire de l Escaut ; vasières mises à nu par la marée basse Administration Pays … Wikipédia en Français
Fonction Publique Française — Pour les autres articles nationaux, voir fonction publique. La fonction publique française regroupe l ensemble des fonctionnaires de France, soit : 1,750 million de fonctionnaires d État selon l INSEE[1] 5,144 millions d agents de la… … Wikipédia en Français
Fonction publique (France) — Fonction publique française Pour les autres articles nationaux, voir fonction publique. La fonction publique française regroupe l ensemble des fonctionnaires de France, soit : 1,750 million de fonctionnaires d État selon l INSEE[1]… … Wikipédia en Français
Fonction publique en France — Fonction publique française Pour les autres articles nationaux, voir fonction publique. La fonction publique française regroupe l ensemble des fonctionnaires de France, soit : 1,750 million de fonctionnaires d État selon l INSEE[1]… … Wikipédia en Français
Fonction publique francaise — Fonction publique française Pour les autres articles nationaux, voir fonction publique. La fonction publique française regroupe l ensemble des fonctionnaires de France, soit : 1,750 million de fonctionnaires d État selon l INSEE[1]… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Fonction Centrale