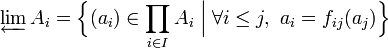Limite Projective

Limite projective

En mathématiques, la notion de limite projective (inverse limit en anglais) est utilisée pour considérer simultanément toute une famille d'objets, par exemple des groupes, liés entre eux par une famille de morphismes, par exemple des morphismes de groupes.

Le cadre général pour cette notion est celui des catégories.

Définition concrète

Pour fixer les idées, on parle d'abord de limite projectives de groupes.

On considère une famille (A_i)_i∈I de groupes, indexée par un ensemble I ordonné, et munie d'une famille de morphismes de groupes f_ij : A_j → A_i pour tout i ≤ j (remarquer l'ordre : du plus grand indice j vers le plus petit i, au contraire d'une limite inductive) vérifiant les conditions de compatibilité :

f_ii est l'identité sur A_i,
f_ik = f_ij O f_jk pour tous i ≤ j ≤ k.

La donnée (I, A_i, f_ij) est appelée système projectif de groupes. La limite projective de ce système est alors définie comme un sous-groupe du produit direct des A_i :

$\varprojlim A_i = \Big\{(a_i) \in \prod_{i\in I}A_i \;\Big|\; \forall i \leq j, \,\, a_i = f_{ij}(a_j) \Big\}$

Cette limite projective est munie naturellement de projections sur chacun des A_i. Qui plus est, elle vérifie une propriété universelle parmi les groupes se projetant sur les A_i. Il est en fait possible de définir la limite projective par cette propriété universelle.

La même construction peut être effectuée avec des ensembles, des anneaux, des modules, des algèbres, au lieu des groupes.

Exemple

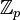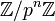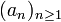L'anneau des entiers p-adiques $\mathbb Z_p$ est défini comme la limite projective des anneaux $\mathbb Z/p^n\mathbb Z$ , indexés par $\mathbb{N}$ et reliés par les morphismes de réduction modulo p. Un entier p-adique est alors une suite $(a_n)_{n\ge 1}$ telle que 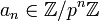$a_n \in \mathbb Z/p^n\mathbb Z$ et que, si $n < m$ , $a_n\equiv a_m [p^n]$ .

Définition générale

Soit (X_i, f_ij) un système projectif dans une catégorie C (la définition donnée ci-dessus pour les groupes s'adapte à n'importe quelle catégorie). La limite projective X est un objet de la catégorie C muni de flèches π_i de X à valeurs dans X_i vérifiant les relations de compatibilité π_i = f_ij O π_j pour tous i ≤ j. De plus, la donnée (X, π_i) doit être universelle : pour tout autre objet Y muni d'une famille de flèches ψ_i il existe une unique flèche u : Y → X telle que le diagramme :

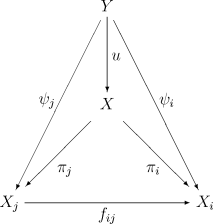
soit commutatif pour tous i ≤ j. La limite projective est notée : 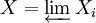$X = \varprojlim X_i$ . On parlera de limite projective des X_i suivant les morphismes f_ij, ou par abus de langage, de limite suivant I, voire tout simplement de limite projective des X_i.

Contrairement au cas concret de la catégorie des groupes, où la définition comme sous-groupe du produit direct assure l'existence d'une limite projective, la limite projective peut ne pas exister dans une catégorie générale. En revanche, l'unicité si existence est toujours assurée : si X′ est une autre limite projective, il existe un unique isomorphisme X′ → X qui commute avec les projections.

Voir aussi

Portail des mathématiques

Ce document provient de « Limite projective ».

Catégorie : Théorie des catégories

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Limite Projective de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Limite projective — En mathématiques, formalisée dans le langage des catégories, la limite projective est une généralisation du produit. Cette notion est duale de celle de limite inductive. Sommaire 1 Limite projective d ensembles 2 Système projectif … Wikipédia en Français
Limite Inductive — En mathématiques, la notion de limite inductive (parfois appelée limite directe, suivant l anglais direct limit) est utilisée pour considérer simultanément toute une famille d objets, par exemple des groupes, liés entre eux par une famille de… … Wikipédia en Français
Limite inductive — Sommaire 1 Avant propos 2 Ensemble ordonné filtrant 3 Système inductif 4 Propriété universelle de la limite inductive … Wikipédia en Français
Concept De Limite (Psychanalyse) — Comme l hystérie fut à la mode aux premiers moments de Sigmund Freud et point de départ de toute l œuvre freudienne, les frontières, limites, seuils et bifurcations le sont dans les années 1970 90. La frontière et le seuil sont ce qui relie et… … Wikipédia en Français
Concept de limite (psychanalyse) — La limite apparaît comme une zone grise entre le blanc et le noir et non pas une ligne de démarcation nette et claire. La notion paradoxale d interface est représentative du concept de limite. Cette notion est paradoxale dans la mesure où elle… … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
TOPOLOGIQUES (ESPACES VECTORIELS) — La théorie des espaces normés, développée par S. Banach et ses élèves, s’est vite révélée insuffisante pour les besoins de l’analyse fonctionnelle où interviennent de nombreux espaces vectoriels munis d’une topologie qui n’est pas déduite d’une… … Encyclopédie Universelle
SYSTÈMES DYNAMIQUES DIFFÉRENTIABLES — Sans doute née avec le mémoire que Poincaré écrivit en 1881 «sur les courbes définies par des équations différentielles», où l’étude quantitative (analytique) locale des équations différentielles dans le champ complexe est remplacée par leur… … Encyclopédie Universelle
CATÉGORIES ET FONCTEURS — Introduite en 1945 par Eilenberg et MacLane pour rendre compte de propriétés très générales des structures mathématiques, la théorie des catégories a quelque peu pâti, à ses débuts, de cette généralité qui lui valut auprès des «mathématiciens… … Encyclopédie Universelle

Dictionnaires et Encyclopédies sur 'Academic'

Limite Projective