Mesure Finie
- Mesure Finie
-
Mesure finie
Sur un espace mesurable 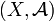 , une mesure finie ou mesure bornée est une mesure (réelle ou complexe) μ dont la masse | μ | (X) (valeur de la variation totale | μ | sur X) est finie.
, une mesure finie ou mesure bornée est une mesure (réelle ou complexe) μ dont la masse | μ | (X) (valeur de la variation totale | μ | sur X) est finie.
Fonctions intégrables
Toute fonction complexe f mesurable et bornée est intégrable contre toute mesure finie μ ; et on dispose de la majoration :
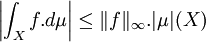
Exemples de mesures finies
- La mesure de comptage sur un ensemble X est finie ssi X est un ensemble fini.
- Les masses de Dirac sont des mesures finies, quel que soit l'espace mesurable considéré.
- Plus généralement, les mesures de probabilité sont des exemples de mesures finies : ce sont des mesures positives de masse 1.
- Pour une mesure complexe ν pas nécessairement finie, et pour une fonction mesurable ν-intégrable, la variation totale de la mesure f.ν est exactement | f | . | ν | ; de fait, la mesure f.ν est finie.
Espace des mesures finies
Toute somme de mesures finies est une mesure finie. Toute mesure proportionnelle à une mesure finie est une mesure finie. Les mesures bornées forment un espace vectoriel complexe 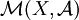 . De plus, on définit la norme :
. De plus, on définit la norme :
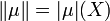
Pour cette norme, c'est un espace de Banach.
Pour toute mesure ν, l'application 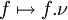 induit une isométrie de
induit une isométrie de 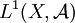 sur un sous-espace vectoriel fermé de
sur un sous-espace vectoriel fermé de 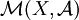 . Ce sous-espace est exactement l'ensemble des mesures finies absolument continues par rapport à ν.
. Ce sous-espace est exactement l'ensemble des mesures finies absolument continues par rapport à ν.
 Portail des mathématiques
Portail des mathématiques
Catégorie : Théorie de la mesure
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Mesure Finie de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Mesure finie — Sur un espace mesurable , une mesure finie ou mesure bornée est une mesure (réelle ou complexe) (en) μ dont la masse | μ | (X) (valeur sur X de la variation |μ| de μ) est finie. Sommaire 1 … Wikipédia en Français
Mesure bornée — Mesure finie Sur un espace mesurable , une mesure finie ou mesure bornée est une mesure (réelle ou complexe) μ dont la masse | μ | (X) (valeur de la variation totale | μ | sur X) est finie. Fonctions intégrables Toute fonction complexe f… … Wikipédia en Français
Mesure (mathematiques) — Mesure (mathématiques) Pour les articles homonymes, voir mesure. En mathématiques, une mesure est une fonction qui associe une « longueur », un « volume » ou encore une « probabilité » à certaines parties d un… … Wikipédia en Français
Mesure (mathématique) — Mesure (mathématiques) Pour les articles homonymes, voir mesure. En mathématiques, une mesure est une fonction qui associe une « longueur », un « volume » ou encore une « probabilité » à certaines parties d un… … Wikipédia en Français
Mesure de dénombrement — Mesure (mathématiques) Pour les articles homonymes, voir mesure. En mathématiques, une mesure est une fonction qui associe une « longueur », un « volume » ou encore une « probabilité » à certaines parties d un… … Wikipédia en Français
Mesure (mathématiques) — Pour les articles homonymes, voir mesure. Pour une introduction à cette notion, consulter l article : Superficie. En mathématiques, une mesure positive (ou simplement mesure quand il n y a pas de risque de confusion) est une fonction qui… … Wikipédia en Français
Mesure sigma-finie — Cet article court présente un sujet plus développé dans : Mesure (mathématiques). Soit un espace mesuré. On dit que la mesure est finie lorsqu il existe un recouvrement dénombrable de X par des sous ensembles de mesure finie. C est à dire,… … Wikipédia en Français
Mesure De Lebesgue — La mesure de Lebesgue doit son nom au mathématicien français Henri Léon Lebesgue. Elle est d une importance capitale en théorie de l intégration. Sommaire 1 Définition formelle 2 Propriétés de la mesure de Lebesgue 3 Tribu de Lebesgue … Wikipédia en Français
Mesure de lebesgue — La mesure de Lebesgue doit son nom au mathématicien français Henri Léon Lebesgue. Elle est d une importance capitale en théorie de l intégration. Sommaire 1 Définition formelle 2 Propriétés de la mesure de Lebesgue 3 Tribu de Lebesgue … Wikipédia en Français
Mesure De Haar — Une mesure de Haar sur un groupe topologique localement compact séparable G est une mesure borélienne positive λ invariante par translation à gauche. Autrement dit, pour toute partie borélienne B de G, et pour tout g dans G, on a : μ(gB) =… … Wikipédia en Français
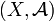 , une mesure finie ou mesure bornée est une mesure (réelle ou complexe) μ dont la masse | μ | (X) (valeur de la variation totale | μ | sur X) est finie.
, une mesure finie ou mesure bornée est une mesure (réelle ou complexe) μ dont la masse | μ | (X) (valeur de la variation totale | μ | sur X) est finie.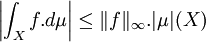
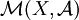 . De plus, on définit la norme :
. De plus, on définit la norme :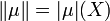
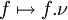 induit une isométrie de
induit une isométrie de 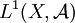 sur un sous-espace vectoriel fermé de
sur un sous-espace vectoriel fermé de 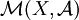 . Ce sous-espace est exactement l'ensemble des mesures finies absolument continues par rapport à ν.
. Ce sous-espace est exactement l'ensemble des mesures finies absolument continues par rapport à ν.