- Groupe Profini
-
Groupe profini
En théorie des groupes, un groupe profini est une généralisation de la notion de groupes finis. Elle est particulièrement utile en théorie de Galois, pour pouvoir travailler avec des extensions infinies.
Par définition, un groupe profini est la limite projective d'un système projectif de groupes finis dont les flèches sont surjectives.
Comme plus généralement pour les catégories, cette limite projective est uniquement définie à unique isomorphisme près. Elle peut être interprétée comme objet final d'une bonne catégorie.
Sommaire
Exemples
L'exemple le plus simple de groupe profini provient certainement de la famille des
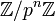, où p est un nombre premier fixé, n variant parmi les entiers naturels. Il est bien connu qu'il existe des morphismes surjectifs 
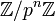pour m plus grand que n ; avec de bonne propriétés de composition entre eux. Un élément du groupe profini associé à ce système projectif est alors la donnée d'une famille (αn)n où chaque αn est dans , et tel que deux coordonnées vérifient toujours : φm,n(αm) = αn. On note 
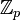ce groupe profini, qui peut par ailleurs être obtenu comme un anneau d'entiers dans la théorie des corps de nombres p-adiques. Ce groupe est en fait le pro-p-complété du groupe des entiers relatifs.En particulier, les entiers relatifs peuvent être vus comme des éléments de ce groupe profini : tout entier peut s'écrire comme une somme finie
α = ∑ aipi i , avec ai inférieur à p. On pose alors
.On peut de même construire le complété profini
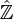du groupe des entiers relatifs en considérant le système projectif formé à partir de tous les 
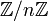.Topologie
Par le théorème de Tychonov, on constate qu'un groupe profini peut être muni d'une topologie qui le rende compact, chacun des groupes finis ayant permis de le construire étant muni de la topologie discrète.
On a en fait la caractérisation suivante : un groupe compact est profini si et seulement s'il est totalement discontinu.
Théorie de Sylow
Les groupes profinis ont une structure suffisamment proche de celle des groupes finis pour que la théorie de Sylow s'y énonce de manière analogue au cas classique ; la démonstration se faisant par un simple passage à la limite.
Théorie de Galois
Un groupe de Galois d'une extension infinie peut facilement être vu comme un groupe profini : en effet, ses quotients finis (qui correspondent via la corrspondance de Galois aux sous-extensions finies), forment un système projectif, dont la limite est le groupe considéré.
Le cas du pro-p-complété
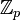de 
apparaît notamment en théorie d'Iwasawa.Bibliographie
- (en) Luis Ribes, Pavel Zalesskii, Profinite groups [détail des éditions]
- (en) John S. Wilson Profinite groups [détail des éditions]
Portail des mathématiques
Catégorie : Théorie des groupes
Wikimedia Foundation. 2010.
