Fonction gaussienne
- Fonction gaussienne
-
 Ne doit pas être confondu avec la fonction d'erreur
Ne doit pas être confondu avec la fonction d'erreur,
également appelée «
fonction de Gauss ».
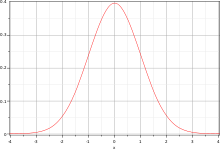
Fonction gaussienne pour μ =
0,
σ =
1 ;
courbe centrée en zéro
Une fonction gaussienne est une fonction en exponentielle de l'opposé du carré de l'abscisse (une fonction en exp( − x2)). Elle a une forme caractéristique de courbe en cloche.
L'exemple le plus connu est la densité de probabilité de la loi normale

où μ est l'espérance mathématique et σ est l'écart type.
La largeur à mi-hauteur (FWHM, full width at half maximum) H vaut

la demi largeur à mi-hauteur vaut donc environ 1,177·σ.
Application
Les fonctions gaussiennes sont très utilisées en physique. En effet, nombre de phénomènes physiques suivent une distribution de type gaussien, expliqué par le théorème de la limite centrale. L'intérêt des fonctions gaussiennes en physique est également dû à certaines de leurs propriétés mathématiques remarquables. Par exemple, la transformée de Fourier d'une fonction gaussienne est une fonction gaussienne, ce qui entraîne notamment le fait que les faisceaux lasers sont des faisceaux gaussiens.
Voir aussi
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Fonction gaussienne de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Fonction Gaussienne — Une fonction gaussienne est une fonction en exponentielle de l opposé du carré de l abscisse (une fonction en exp( (x2)). Elle a une forme caractéristique de courbe en cloche. L exemple le plus connu est la densité de probabilité de la loi… … Wikipédia en Français
Fonction De Voigt — Une fonction de Voigt est le produit de convolution d une fonction gaussienne et d une fonction lorentzienne ayant le même sommet. C est donc une fonction de la forme soit, si le sommet se trouve en 0 (x0 = 0) … Wikipédia en Français
Fonction de voigt — Une fonction de Voigt est le produit de convolution d une fonction gaussienne et d une fonction lorentzienne ayant le même sommet. C est donc une fonction de la forme soit, si le sommet se trouve en 0 (x0 = 0) … Wikipédia en Français
Fonction Lorentzienne — On reconnaît une courbe lorentzienne à la forme suivante : C est l expression la plus simple d une lorentzienne, centrée en x=0. Une forme paramétrée par l abscisse x0 du sommet et la largeur Γ à mi hauteur (couramment appelée largeur de la… … Wikipédia en Français
Fonction de Voigt — Pour les articles homonymes, voir Voigt. Une fonction de Voigt est le produit de convolution d une fonction gaussienne et d une fonct … Wikipédia en Français
Gaussienne — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. En mathématiques Gaussienne se réfère à : Une fonction : la fonction gaussienne ; Une distribution ou loi de probabilité : la loi… … Wikipédia en Français
Fonction d'erreur — Pour les articles homonymes, voir Fonction, Erreur et erf. Construction de la fonction d erreur réelle. En mathématiques, la fonction d erreur (aussi appelée … Wikipédia en Français
Fonction lorentzienne — Pour l’article homonyme, voir Courbe de Lorenz. On reconnaît une courbe lorentzienne à la forme suivante : C est l expression la plus simple d une lorentzienne, centrée en x=0. Une forme paramétrée par l abscisse x0 du sommet et… … Wikipédia en Français
FONCTION D’APPAREIL — Forme particulière de la fonction de transfert pour un spectromètre, la fonction d’appareil est la courbe de transmission globale obtenue en faisant défiler le spectre sur la fente de sortie, la fente d’entrée étant éclairée par une radiation… … Encyclopédie Universelle
Fonction De Pearson — Les fonctions de Pearson ont été crées pour représenter des distributions unimodales. Il en existe douze. Elles ont été inventées par Karl Pearson à la fin du XIXe siècle et au début du XXe siècle. Sommaire 1 Pearson IV … Wikipédia en Français



