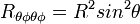- Courbure De Gauss
-
Courbure de Gauss
La courbure de Gauss d'une surface paramétrée X en X(P) est le produit des courbures principales. De manière équivalente, la courbure de Gauss est le déterminant de l'endomorphisme de Weingarten.
Le tableau suivant liste les courbures de Gauss de surfaces remarquables :
- plan : courbure nulle
- sphère de rayon R, courbure
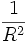
Le calcul de la courbure de Gauss est particulièrement compliqué [1] [2] mais se simplifie considérablement en coordonnées de Riemann.
Sommaire
Coordonnées normales de Riemann
Nous utilisons, à l'endroit où nous sommes sur Terre, les coordonnées cartésiennes. Ailleurs nous devons utiliser des coordonnées ayant subi une rotation fonction de la latitude et de la longitude. Il est bien connu que les Australiens ont la tête en bas sans être gênés. C'est pourquoi les coordonnées de Riemann sont qualifiées de locales. Les coordonnées de Riemann sont pratiquement des coordonnées cartésiennes dans le plan tangent à la Terre et, plus généralement à une surface ou un espace courbe.
En coordonnées de Gauss (on doit normalement utiliser u et v au lieu de x et y), la métrique s'écrit:
Pour passer en coordonnées de Riemann, on doit diagonaliser la matrice représentative de la métrique puis changer les échelles des axes de coordonnées pour obtenir une métrique euclidienne:
La courbure de Gauss étant le produit des courbures principales kx et ky et la courbure d'une courbe plane étant la dérivée seconde de l'ordonnée z par rapport à l'abscisse x ou y, on a:
Courbure de Gauss en coordonnées de Riemann
Considérons une surface en un point O, origine des coordonnées, et le plan tangent à la surface en O. L’axe Oz est perpendiculaire au plan tangent où nous choisissons des axes Ox et Oy rectangulaires dans le plan tangent coïncidant avec les directions principales de la surface. Au voisinage de O, les coordonnées x et y dans le plan tangent sont très voisines des coordonnées de Gauss u et v sur la surface courbe de sorte que nous n’utiliserons que les coordonnées cartésiennes x et y dans le plan tangent et z, cote par rapport au plan tangent. Considérons une surface courbe d’équation z(x,y)=0 dont la différentielle est
La métrique de l’espace euclidien à trois dimensions est
En y remplaçant dz par son expression ci-dessus, la métrique devient
La formule générique de la métrique d’une surface est:
où les coefficients gij de la métrique sont des nombres sans dimension. On calcule les dérivées secondes de gxx et gyy, respectivement par rapport à y et à x :
Faisons la somme de ces deux équations :
Dérivons maintenant gxy = 0, puisque la métrique est diagonale par hypothèse :
ce qui donne l'équation :
Le membre de droite, entre crochets, de cette expression, identique au terme entre crochets précédent peut donc être remplacé. D’où
Dans cette formule il n’y a que des dérivées secondes des coefficients de la métrique et de z par rapport à x et à y, en conformité avec l’hypothèse des coordonnées de Riemann. Approximons, au point considéré, la surface par un paraboloïde de courbures principales kx et ky dont les plans principaux coïncident avec ceux de la surface courbe :
Comme il n’y a pas de terme rectangle dans cette expression, on a
Les coefficients kx et ky sont les dérivées secondes de z par rapport à x et y et, donc, les courbures des paraboles, intersections du paraboloïde avec ses plans principaux. Comme le produitK = kxky des courbures principales est, par définition, la courbure de Gauss, on peut écrire :
En utilisant les deux relations précédentes, on obtient la courbure de Gauss en coordonnées de Riemann:
On remarquera que la virgule indique une dérivation partielle, ce qui permet de rendre les équations plus lisibles. La courbure de Gauss, qui a pour dimension l’inverse du carré d’une longueur, devient très simple en coordonnées normales de Riemann, en approximant la surface par un paraboloïde dont les axes de symétrie coïncident avec les directions principales de la métrique. Elle est alors égale au tenseur de Riemann Rxyxyde la surface.
Courbure de Gauss en coordonnées de Gauss
Le calcul étant compliqué, nous nous contenterons de donner quelques formules pratiques. La première correspond à une métrique diagonale[3] :
La notation de Leibniz est remplacée par des virgules indiquant une dérivation partielle. On y reconnaît les deux premiers termes identiques à ceux de l'expression en coordonnées de Riemann au coefficient multiplicateur près guugvv, différent de un en coordonnées de Gauss.
Les x et y (ou u et v) étant en réalité des coordonnées de Gauss, on peut les remplacer par θ et φ, coordonnées sur la sphère:
La formule de Brioschi donne la courbure et le tenseur de Riemann Ruvuv sous forme matricielle pour une métrique diagonale :
où E = guu,G = gvv,F = guv (notation de Gauss). Les indices représentent une dérivée partielle simple ou double par rapport aux coordonnées de Gauss u et v, correspondant aux x et y précédents.
Application à la sphère
Courbure de Gauss de la sphère en coordonnées de Riemann
L’équation d’une sphère de rayon R en coordonnées cartésiennes dans l’espace euclidien à trois dimensions est
- x2 + y2 + z2 = R2.
Pour que la concavité soit positive, on doit prendre la racine négative pour z :
Développons-la en série au pôle Sud, au voisinage de x = y = 0, c’est-à-dire en coordonnées de Riemann :
D'où par différentiation :
La métrique de l’espace euclidien à trois dimensions
devient celle d’un paraboloïde de révolution approximant la sphère :
Plus près du pôle Sud, où x ≈ y ≈ 0, la métrique est euclidienne en éliminant les termes du second ordre. Pour la mettre en coordonnées de Riemann il est nécessaire de la diagonaliser. Il est plus simple d'utiliser les coordonnées sphériques qui donnent une métrique diagonale. Pour être en coordonnées de Riemann, on diagonalise la métrique, qui devient :
où K = kxky est la courbure de Gauss. On retrouve la métrique euclidienne en O où x et y sont nuls. Dans cette expression, on a gxx = 1, gxy = 0 et
On retrouve bien la courbure de Gauss de la sphère, égale au tenseur de Riemann Ruvuv mais uniquement en coordonnées de Riemann.
Courbure de Gauss de la sphère en coordonnées de Gauss
Considérons un petit rectangle élémentaire sur la sphère de rayon R. Soit θ la colatitude et φ la longitude. Sa diagonale ds est, en vertu du théorême de Pythagore:
La métrique de la sphère est diagonale, sans terme rectangle :
La formule générale de la courbure de Gauss en coordonnées de Gauss pour une métrique diagonale :
se simplifie sur la sphère en éliminant les termes nuls :
puis, en explicitant les coefficients de la métrique :
et enfin en :
Le tenseur de Riemann de la sphère est
Références
- ↑ Struik, D.J., Lectures on Classical Differential Geometry, Dover, 1988.
- ↑ Bernard Schaeffer, Relativités et quanta clarifiés, Publibook, 2007
- ↑ Brown, Kevin, « Reflections on Relativity »
- ↑ Keyszig,E, Differential geometry, Dover, 1991
- ↑ Audin, M, Géométrie, EDP Sciences 2006
- ↑ (en) Gaussian curvature sur Wikipedia
Voir aussi
- Portail de la géométrie
Catégories : Surface | Carl Friedrich Gauss
Wikimedia Foundation. 2010.


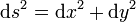

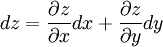
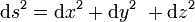
![\mathrm ds^2= \left[1+\left(\frac{\partial z}{\partial x}\right)^2\right]dx^2 + 2\frac{\partial z}{\partial x}\frac{\partial z}{\partial y}dx dy + \left[1+\left(\frac{\partial z}{\partial y}\right)^2\right]dy^2](/pictures/frwiki/52/40b4069065da45b32592d9b9205e5d7f.png)
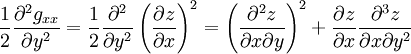
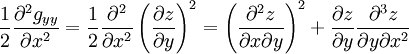
![\frac12 \frac{\partial^2 g_{xx}}{\partial y^2}+\frac12 \frac{\partial^2 g_{yy}}{\partial x^2}
=\left(\frac{\partial^2 z}{\partial x\partial y}\right)^2 +\left[\frac{\partial z}{\partial x}\frac{\partial^3 z}{\partial x\partial y^2}
+\left(\frac{\partial^2 z}{\partial x\partial y}\right)^2 +\frac{\partial z}{\partial y}\frac{\partial^3 z}{\partial y\partial x^2}\right]](/pictures/frwiki/50/2055b3c3642a9cc8fc7e816f0e7b9d2f.png)
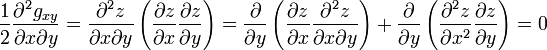
![\frac{\partial^2 z}{\partial x^2}\frac{\partial^2 z}{\partial y^2} = -\left[\left(\frac{\partial^2 z}{\partial x\partial y}\right)^2
+\frac{\partial z}{\partial x}\left(\frac{\partial^3 z}{\partial y\partial x^2}\right)
+\frac{\partial z}{\partial y}\left(\frac{\partial^3 z}{\partial x\partial y^2}\right)\right]](/pictures/frwiki/51/3dcb329584171ccd379d49f4111319a2.png)

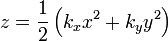
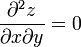
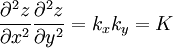
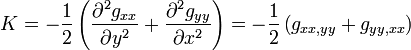
![K= \frac{1}{g_{uu}g_{vv}} \left[
-\frac12 \left(g_{uu,vv}+g_{vv,uu}\right)
+\frac{g_{uu,v}^2}{4g_{uu}}+\frac{g_{vv,u}^2}{4g_{vv}}
+\frac{g_{uu,u}^2g_{vv,u}}{4g_{uu}}+\frac{g_{vv,v}^2g_{uu,v}}{4g_{vv}}
\right]](/pictures/frwiki/98/b98949e493ed2b9a5bf7e5a2ca71dbed.png)
![K= \frac{1}{g_{\theta\theta}g_{\phi\phi}} \left[
-\frac12 \left(g_{\theta\theta,\phi\phi}+g_{\phi\phi,\theta\theta}\right)
+\frac{g_{\theta\theta,\phi}^2}{4g_{\theta\theta}}+\frac{g_{\phi\phi,\theta}^2}{4g_{\phi\phi}}
+\frac{g_{\theta\theta,\theta}^2g_{\phi\phi,\theta}}{4g_{\theta\theta}}+\frac{g_{\phi\phi,\phi}^2g_{\theta\theta,\phi}}{4g_{\phi\phi}}
\right]](/pictures/frwiki/55/7b021b12e7f205e9c176506f52b8a75e.png)
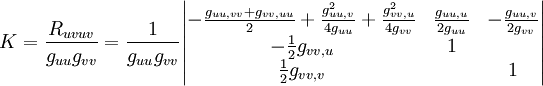
![K = \frac{1} {(EG-F^2)^2}\left[
\begin{vmatrix} -\frac{1}{2}E_{vv} + F_{uv} - \frac{1}{2}G_{uu} & \frac{1}{2}E_u & F_u-\frac{1}{2}E_v\\F_v-\frac{1}{2}G_u & E & F\\\frac{1}{2}G_v & F & G \end{vmatrix}-\begin{vmatrix} 0 & \frac{1}{2}E_v & \frac{1}{2}G_u\\\frac{1}{2}E_v & E & F\\\frac{1}{2}G_u & F & G \end{vmatrix}\right]](/pictures/frwiki/50/2cb397604db9faab9261412b16394047.png)

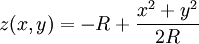
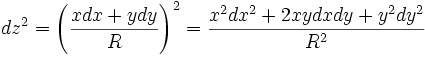
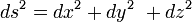
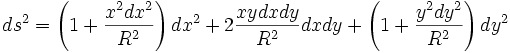
![ds^2= dx^2 + \left[1 - \frac{ x^2 + y^2}{R^2}\right] dy^2](/pictures/frwiki/97/a9ff6dd4adf330fa6fa219c5311763ca.png)
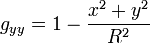
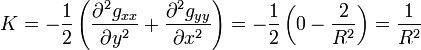
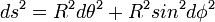
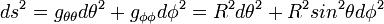
![K= \frac{1}{g_{\theta\theta}g_{\phi\phi}}
\left[
-\frac12 \left(0+g_{\phi\phi,\theta\theta}\right)
+0+\frac{g_{\phi\phi_,\theta}^2}{4g_{\phi\phi}}
+0+0
\right]](/pictures/frwiki/97/a92a9593d9ee8cba60c918a7c95dd6f7.png)
![K= \frac{1}{R^4sin^2\theta} \left[
-\frac12 \times 2R^2 (sin\theta cos\theta)_{,\theta}
+\frac{4R^4sin^2 \theta cos^2 \theta}{4R^2sin^2\theta}
\right]](/pictures/frwiki/97/a429e5fa33470fc536765e42936e5e1a.png)
![K= \frac{1}{R^2sin^2\theta} \left[
-\left(cos^2\theta-sin^2\theta \right)
+\frac{sin^2 \theta cos^2 \theta}{sin^2\theta}
\right]= \frac{1}{R^2}](/pictures/frwiki/54/66f24e440ea80fc74ba0038f1ab3d73c.png)