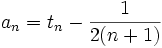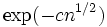- Operateur de Gauss-Kuzmin-Wirsing
-
Opérateur de Gauss-Kuzmin-Wirsing
En mathématiques, l'opérateur de Gauss-Kuzmin-Wirsing apparaît dans l'étude des fractions continues. Il est aussi relié à la fonction zêta de Riemann.
Sommaire
Introduction
L'opérateur de Gauss-Kuzmin-Wirsing est l'opérateur de transfert de l'application de Gauss
Cette opérateur agit sur les fonctions comme
La fonction propre zéro-ième de cet opérateur est
qui correspond à la valeur propre de 1. Cette fonction propre donne la probabilité d'occurrence d'un entier donné dans un développement en fraction continue, et est connue sous le nom de distribution de Gauss-Kuzmin. Ceci en découle en partie parce que l'application de Gauss agit comme un opérateur de décalage troncaturant les fractions continues : si
![x=[0;a_1,a_2,a_3,\ldots]\,](/pictures/frwiki/97/a99f8c05c1ae8a36758b9971f2a10f7a.png)
est la représentation en fraction continue d'un nombre 0 ; x ; 1, alors ![h(x)=[0;a_2,a_3,\ldots]\,](/pictures/frwiki/50/255568adf8387c683ac576ed13cd9532.png)
.Les valeurs propres supplémentaires peuvent être calculées numériquement ; la valeur propre suivante est
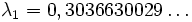et est connue sous le nom de constante de Gauss-Kuzmin-Wirsing. Les formes analytiques pour les valeurs propres supplémentaires ne sont pas connues. On ignore si les valeurs propres sont irrationnelles.Relation avec la fonction zêta de Riemann
L'opérateur GKW est relié à la fonction zêta de Riemann. La fonction zêta peut être écrite sous la forme
ce qui implique que
par un changement de variables.
Eléments matriciels
Considérons les développement en série de Taylor au point x=1 pour une fonction f(x) et g(x) = [Gf](x). C'est-à-dire, soit
et écrivons de même pour g(x). Le développement est fait par rapport à x=1 parce que l'opérateur GKW n'a pas un bon comportement au point x=0. Le développement est fait pour 1-x donc, nous pouvons garder x avec un nombre positif,
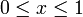. Alors, l'opérateur GKW agit sur les coefficient de Taylor commeoù les éléments matriciels de l'opérateur GKW sont donnés par
Cet opérateur est extrêmement bien formé, et ainsi il peut être suivi numériquement. Chaque entrée est une série zêta rationnelle finie. La constante de Gauss-Kuzmin est facilement calculée avec une grande précision en diagonalisant numériquement la partie supérieure gauche n x n. Il n'existe pas d'expression connue qui diagonalise cet opérateur ; il n'existe pas d'expression finie connue pour les valeurs propres ou les vecteurs propres.
La fonction zêta de Riemann
La fonction zêta de Riemann peut être écrite sous la forme
où le
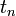est donné par les éléments matriciels ci-dessus :
.
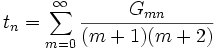En effectuant les sommations, on obtient :
où
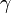est la constante d'Euler-Mascheroni. Ces 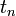joue un rôle analogue aux constantes de Stieltjes, mais pour le développement en factorielles décroissantes. En écrivanton obtient :
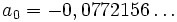et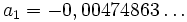 
et ainsi de suite. Les valeurs deviennent petites rapidement mais sont oscillatoires. Certaines sommes explicites sur ces valeurs peuvent être exécutées. Elles peuvent être reliées explicitement aux constantes de Stieltjes en réexprimant la factorielle décroissante comme un polynôme avec les coefficients en nombre de Stirling, puis en le résolvant. Plus généralement, la fonction zêta de Riemann peut être réexprimée comme un développement en termes de suites de Sheffer de polynômes.Le développement de la fonction zêta de Riemann relaté ici sous forme de « factorielle descendante », a été introduit et complètement étudié dans :
- A. Yu. Eremin, I. E. Kaporin, and M. K. Kerimov, The calculation of the Riemann zeta-function in the complex domain, U.S.S.R. Comput. Math. and Math. Phys. 25 (1985), no. 2, 111--119
- A. Yu. Yeremin, I. E. Kaporin, and M. K. Kerimov, Computation of the derivatives of the Riemann zeta-function in the complex domain, U.S.S.R. Comput. Math. and Math. Phys. 28 (1988), no. 4, 115--124
Le dernier article contient une démonstration concernant le comportement asymptotique des coefficients du développement. Les coefficients sont décroissants comme
où
est une constante positive.Références
- A. Ya. Khinchin, Continued Fractions, 1935, English translation University of Chicago Press, 1961 ISBN 0-486-69630-8 (See section 15).
- K. I. Babenko, On a Problem of Gauss, Soviet Mathematical Doklady 19:136-140 (1978) MR 57 #12436
- K. I. Babenko and S. P. Jur'ev, On the Discretization of a Problem of Gauss, Soviet Mathematical Doklady 19:731-735 (1978). MR 81h:65015
- Keith Briggs, A precise computation of the Gauss-Kuzmin-Wirsing constant (2003) (Contains a very extensive collection of references.)
- A. Durner, On a Theorem of Gauss-Kuzmin-Lévy. Arch. Math. 58, 251-256, (1992). MR 93c:11056
- Phillipe Flajolet and Brigitte Vallée, On the Gauss-Kuzmin-Wirsing Constant (1995).
- A. J. MacLeod, High-Accuracy Numerical Values of the Gauss-Kuzmin Continued Fraction Problem. Computers Math. Appl. 26, 37-44, (1993).
- E. Wirsing, On the Theorem of Gauss-Kuzmin-Lévy and a Frobenius-Type Theorem for Function Spaces. Acta Arith. 24, 507-528, (1974). MR 49 #2637
- Linas Vepstas The Bernoulli Operator, the Gauss-Kuzmin-Wirsing Operator, and the Riemann Zeta (2004) (PDF)
Portail des mathématiques
Catégories : Fonction zêta | Fraction continue | Carl Friedrich Gauss
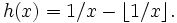
 = \sum_{n=1}^\infty \frac {1}{(x+n)^2} f \left(\frac {1}{x+n}\right).](/pictures/frwiki/48/094d61119473a3dc1587af76fcbbe470.png)
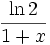
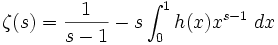
![\zeta(s)=\frac{s}{s-1}-s\int_0^1 dx\; x \left[Gx^{s-1} \right]](/pictures/frwiki/50/20fc4a2b408bcde3ff00648e8a7902fd.png)
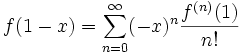
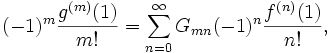
![G_{mn}=\sum_{k=0}^n (-1)^k {n \choose k} {k+m+1 \choose m} \left[ \zeta (k+m+2)- 1\right].](/pictures/frwiki/101/e69af77408134032391227bb882e0d6e.png)
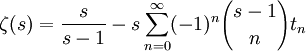
![t_n=1-\gamma + \sum_{k=1}^n (-1)^n {n \choose k} \left[ \frac{1}{k} + \frac {\zeta(k+1)} {k+1} \right]](/pictures/frwiki/51/34d7f70088ede89aca2b30982fe25322.png)
Wikimedia Foundation. 2010.
