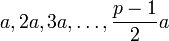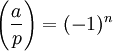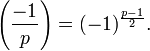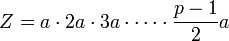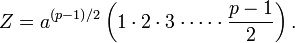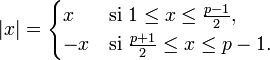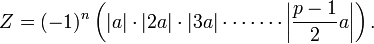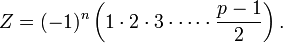Lemme de Gauss (theorie des nombres)

Lemme de Gauss (theorie des nombres)

Lemme de Gauss (théorie des nombres)

Page d'aide sur l'homonymie Pour les articles homonymes, voir Théorème de Gauss.

Un lemme de Gauss est utilisé en théorie des nombres dans certaines démonstrations de la loi de réciprocité quadratique [1].

Pour n'importe quel nombre impair p, soit a un entier qui est relativement premier à p.

On considère les entiers

a, 2a, 3a, \dots, \frac{p-1}{2}a

et leurs plus faibles résidus modulo m.

Soit n le nombre de ces résidus qui sont plus grands que p/2. Alors

\left(\frac{a}{p}\right) = (-1)^n

où \left(\frac{a}{p}\right) est le symbole de Legendre.

Ceci peut, par exemple, être appliqué immédiatement quand a = −1, donnant

\left(\frac{-1}{p}\right) = (-1)^\frac{p-1}{2}.

D'un point de vue plus sophistiqué, ceci est un cas de transfert.

Preuve

Une preuve assez simple de ce lemme peut être déduite du principe utilisé pour la démonstration du petit théorème de Fermat. Pour cela, évaluons le produit suivant :

Z = a \cdot 2a \cdot 3a \cdot \cdots \cdot \frac{p-1}2 a

modulo p de deux manières différentes.

Premièrement, ce produit vaut :

Z = a^{(p-1)/2} \left(1 \cdot 2 \cdot 3 \cdot \cdots \cdot \frac{p-1}2 \right).

Le second calcul est plus délicat. Si x est un résidu non nul modulo p, définissions la "valeur absolue" de x comme

|x| = \begin{cases} x & \mbox{si } 1 \leq x \leq \frac{p-1}2, \\ -x & \mbox{si } \frac{p+1}2 \leq x \leq p-1. \end{cases}

Comme n dénombre les multiples ka se trouvant dans le second intervalle, et que pour ces multiples, −ka se trouve dans le premier intervalle, on a :

Z = (-1)^n \left(|a| \cdot |2a| \cdot |3a| \cdot \cdots \cdots \left|\frac{p-1}2 a\right|\right).

Maintenant, observons que les valeurs |ra| sont distinctes pour r = 1, 2, ..., (p−1)/2. En effet, si |ra| = |sa|, alors ra = ±sa, et donc r = ±s (parce que a est inversible modulo p), donc r = s car ils appartiennent tous deux à l'intervalle 1 ≤ r ≤ (p−1)/2. Mais il y en a exactement (p−1)/2, donc cette séquence représente une permutation des entiers 1, 2, ..., (p−1)/2. On obtient :

Z = (-1)^n \left(1 \cdot 2 \cdot 3 \cdot \cdots \cdot \frac{p-1}2\right).

En comparant avec notre premier calcul, on peut supprimer les facteurs non nuls :

1 \cdot 2 \cdot 3 \cdot \cdots \cdot \frac{p-1}2

ce qui nous donne

a(p − 1) / 2 = ( − 1)n.

Ceci est le résultat souhaité, car la partie de gauche n'est qu'une réécriture du symbole de Legendre (a/p).

Références

  1. ↑ Lemmermeyer1

Liens externes

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Lemme de Gauss (th%C3%A9orie des nombres) ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Lemme de Gauss (theorie des nombres) de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Lemme de gauss (théorie des nombres) — Pour les articles homonymes, voir Théorème de Gauss. Un lemme de Gauss est utilisé en théorie des nombres dans certaines démonstrations de la loi de réciprocité quadratique [1]. Pour n importe quel nombre impair p, soit a un entier qui est… …   Wikipédia en Français

  • Lemme de Gauss (théorie des nombres) — Pour les articles homonymes, voir Théorème de Gauss. Le lemme de Gauss en théorie des nombres donne une condition pour qu un entier soit un résidu quadratique. Il a été introduit et démontré par Gauss dans ses preuves de la loi de réciprocité… …   Wikipédia en Français

  • NOMBRES (THÉORIE DES) - Nombres algébriques — Les mathématiciens grecs avaient découvert que certains rapports de grandeurs ne sont pas rationnels, c’est à dire qu’ils ne sont pas égaux au rapport de deux entiers: il en est ainsi du rapport de la diagonale d’un carré à son côté, puisque… …   Encyclopédie Universelle

  • Lemme de Gauss — (théorie des nombres) Pour les articles homonymes, voir Théorème de Gauss. Un lemme de Gauss est utilisé en théorie des nombres dans certaines démonstrations de la loi de réciprocité quadratique [1]. Pour n importe quel nombre impair p, soit a un …   Wikipédia en Français

  • Liste Des Matières De La Théorie Des Nombres — Article détaillé : cryptologie. . Sommaire 1 Facteur (mathématiques) 2 Fractions 3 Arithmétique modulaire 4 …   Wikipédia en Français

  • Liste des matieres de la theorie des nombres — Liste des matières de la théorie des nombres Article détaillé : cryptologie. . Sommaire 1 Facteur (mathématiques) 2 Fractions 3 Arithmétique modulaire 4 …   Wikipédia en Français

  • Liste des matières de la théorie des nombres — Article détaillé : cryptologie. . Sommaire 1 Facteur (mathématiques) 2 Fractions 3 Arithmétique modulaire 4 Test de primalité e …   Wikipédia en Français

  • Lemme de Gauss (polynômes) — Pour les articles homonymes, voir Théorème de Gauss. En mathématiques il existe un résultat appelé lemme de Gauss s appliquant à la théorie des polynômes. Il énonce que si un polynôme P à coefficients entiers est factorisé en deux polynômes à… …   Wikipédia en Français

  • Theorie algebrique des nombres — Théorie algébrique des nombres En mathématiques, la théorie algébrique des nombres est la branche de l arithmétique utilisant des outils issus de l algèbre pour mieux comprendre les nombres. Son origine est l étude des nombres entiers et… …   Wikipédia en Français

  • Théorie algébrique des nombres — En mathématiques, la théorie algébrique des nombres est la branche de l arithmétique utilisant des outils issus de l algèbre pour mieux comprendre les nombres. Son origine est l étude des nombres entiers et particulièrement les équations… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”