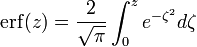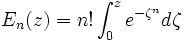Fonction D'erreur

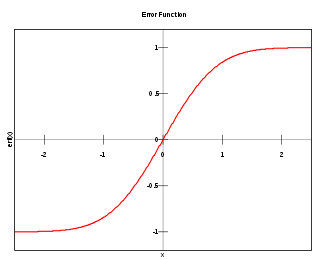
Fonction d'erreur

Pour les articles homonymes, voir Fonction, Erreur et erf.

Construction de la fonction d'erreur réelle.

En mathématiques, la fonction d'erreur (aussi appelée fonction d'erreur de Gauss) est une fonction utilisée en analyse. Cette fonction se note erf et fait partie des fonctions spéciales.

$\operatorname{erf}(z) = \frac{2}{ \sqrt{\pi} } \int_0^z e^{- \zeta^2 } d\zeta$

Intérêt de cette fonction

La probabilité pour qu'une variable normale centrée réduite X prenne une valeur dans l'intervalle [-z, z] est

$\operatorname{erf}\left(\frac{z}{\sqrt{2}}\right)=\mathbb{P}(X\in[-z, z]).$

La fonction de répartition de X, ou fonction de répartition de la loi normale, usuellement notée Φ, est liée à la fonction d'erreur par la relation :

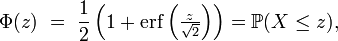
$\Phi(z)\ =\ \frac12\left(1+\operatorname{erf}\left(\tfrac{z}{\sqrt{2}}\right)\right)=\mathbb{P}(X\le z),$

ou bien encore

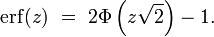
$\operatorname{erf}(z)\ =\ 2\Phi\left(z\sqrt{2}\right)-1.$

La fonction d'erreur intervient également dans l'expression des solutions de l'équation de la chaleur, quand les conditions aux bords sont données par la fonction de Heaviside.

Calcul numérique

L'intégrale ne peut être obtenue à partir d'une formule fermée mais par un développement en série entière intégré termes à termes. Il existe des tables donnant des valeurs des intégrales, comme fonctions de z, mais aujourd'hui, la plupart des logiciels de calcul numérique (tableurs, Scilab) ou de calcul formel (comme Maple ou MuPAD) intègrent une routine de calcul de erf(x) et de sa réciproque, inverf(x), encore plus utile en calcul de probabilités.

Toutefois, les approximations suivantes peuvent être utiles si l'on programme soi-même une application en langage C ou Fortran :

En 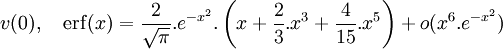$v(0),\quad \operatorname{erf}(x) = \frac{2}{\sqrt{\pi}}.e^{-x^2}. \left ( x + \frac{2}{3} .x^3 + \frac{4}{15} .x^5\right ) + o( x^6.e^{-x^2} )$ (avec une erreur inférieure à 6 × $10 - 4$ pour x < 0,50)

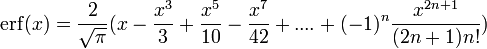$\operatorname{erf}(x) = \frac{2}{\sqrt{\pi}}( x - \frac{x^3}{3} + \frac{x^5}{10} - \frac{x^7}{42} + .... + (-1)^n \frac{x^{2n+1}}{(2n+1)n!})$ (Développement en série de Taylor)

En 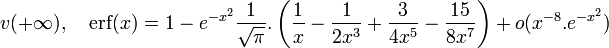$v(+\infty),\quad \operatorname{erf}(x) = 1 - e^{-x^2}\frac{1}{\sqrt{\pi}}. \left ( \frac{1}{x} - \frac{1}{2x^3} + \frac{3}{4x^5} - \frac{15}{8x^7} \right ) + o( x^{-8}.e^{-x^2} )$ (avec une erreur inférieure à 2 × $10 - 4$ pour x > 1,75)
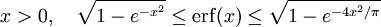
Pour $x>0,\quad \sqrt{ 1-e^{-x^2} } \leq \operatorname{erf}(x) \leq \sqrt{1-e^{-4x^2 / \pi}}$

(encadrement proposé par J. T. Chu, 1955 ; la borne supérieure approche partout la fonction erf à moins de 7 × $10 - 3$ près).

Extensions

Il arrive que la fonction plus générale $E n$ définie par :

$E_n(z) = n! \int_0^z e^{-\zeta^n}d\zeta$

soit utilisée et E₂ est appelée erreur intégrale.

D'autres fonctions d'erreurs utilisées en analyse, notamment :

La fonction d'erreur complémentaire notée erfc et définie par :

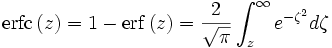
$\operatorname{erfc}\left( z \right) = 1 - \operatorname{erf}\left( z \right) = \frac{2}{ \sqrt{\pi} }\int_z^{\infty}e^{-\zeta^2}d\zeta$

La fonction ierfc, (opposée de l') intégrale de la fonction d'erreur complémentaire erfc :

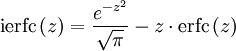
$\operatorname{ierfc}\left( z \right) = \frac{e^{-z^2}}{\sqrt{\pi}} - z\cdot\operatorname{erfc}\left( z\right)$

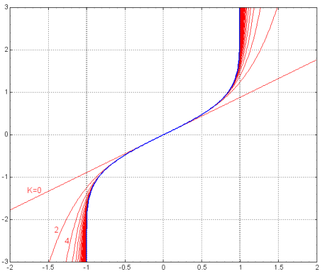
Fonction réciproque

Approximations de la fonction d'erreur réciproque (somme jusqu'à k=K)

La fonction d'erreur réciproque intervient parfois dans des formules statistiques. Elle peut être décrite à l'aide d'un développement en séries:

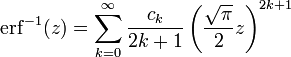
$\operatorname{erf}^{-1}(z)=\sum_{k=0}^\infin\frac{c_k}{2k+1}\left (\frac{\sqrt{\pi}}{2}z\right )^{2k+1}$

où c0 = 1 et

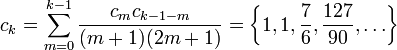
$c_k=\sum_{m=0}^{k-1}\frac{c_m c_{k-1-m}}{(m+1)(2m+1)} = \left\{1,1,\frac{7}{6},\frac{127}{90},\ldots\right\}$

On obtient le développement suivant:

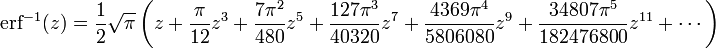
$\operatorname{erf}^{-1}(z)=\frac{1}{2}\sqrt{\pi}\left (z+\frac{\pi}{12}z^3+\frac{7\pi^2}{480}z^5+\frac{127\pi^3}{40320}z^7+\frac{4369\pi^4}{5806080}z^9+\frac{34807\pi^5}{182476800}z^{11}+\cdots\right )$

Voir aussi

Pages liées

Références

Milton Abramowitz et Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972. (Voir Chapitre 7)

Liens externes

MathWorld - Erf

Portail des mathématiques

Ce document provient de « Fonction d%27erreur ».

Catégories : Fonction remarquable | Carl Friedrich Gauss | Fonctions spéciales

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonction D'erreur de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

Fonction d'erreur — Pour les articles homonymes, voir Fonction, Erreur et erf. Construction de la fonction d erreur réelle. En mathématiques, la fonction d erreur (aussi appelée … Wikipédia en Français
Fonction d'erreur de Gauss — Fonction d erreur Pour les articles homonymes, voir Fonction, Erreur et erf. Construction de la fonction d erreur réelle. En … Wikipédia en Français
Fonction de Gauss — Fonction d erreur Pour les articles homonymes, voir Fonction, Erreur et erf. Construction de la fonction d erreur réelle. En … Wikipédia en Français
ERREUR — La définition classique de la vérité et de l’erreur est celle d’Aristote: «Dire de ce qui est qu’il est, ou de ce qui n’est pas qu’il n’est pas, c’est dire vrai; dire de ce qui n’est pas qu’il est ou de ce qui est qu’il n’est pas, c’est dire faux … Encyclopédie Universelle
Erreur commise — Erreur Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom … Wikipédia en Français
Erreur théologique — Erreur Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom … Wikipédia en Français
Fonction De Mittag-Leffler — En mathématiques, la fonction de Mittag Leffler, notée Eαβ qui tient son nom du mathématicien Gösta Mittag Leffler, est une fonction spéciale, c’est à dire qui ne peut être calculée à partir d équations rationnelles, qui s applique dans le plan… … Wikipédia en Français
Fonction de mittag-leffler — En mathématiques, la fonction de Mittag Leffler, notée Eαβ qui tient son nom du mathématicien Gösta Mittag Leffler, est une fonction spéciale, c’est à dire qui ne peut être calculée à partir d équations rationnelles, qui s applique dans le plan… … Wikipédia en Français
Fonction Gaussienne — Une fonction gaussienne est une fonction en exponentielle de l opposé du carré de l abscisse (une fonction en exp( (x2)). Elle a une forme caractéristique de courbe en cloche. L exemple le plus connu est la densité de probabilité de la loi… … Wikipédia en Français
Fonction de Dawson — La fonction de Dawson, F(x), près de l origine … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Fonction D'erreur