- Fonction De Voigt
-
Fonction de Voigt
Une fonction de Voigt est le produit de convolution d'une fonction gaussienne et d'une fonction lorentzienne ayant le même sommet. C'est donc une fonction de la forme
soit, si le sommet se trouve en 0 (x0 = 0) :
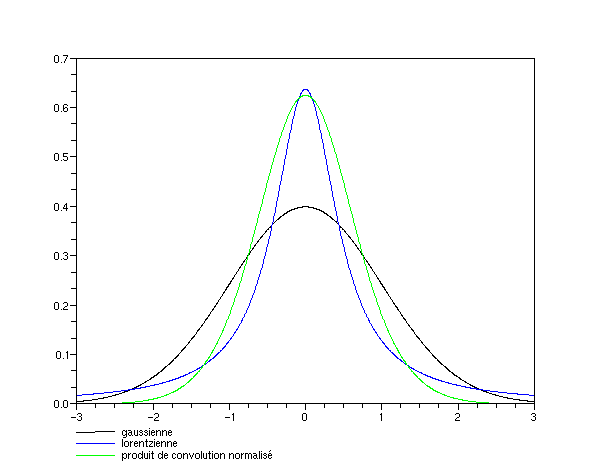
Sommaire
Applications
En spectrométrie d'émission ou d'absorption, une raie correspond à l'énergie de transition entre deux niveaux électroniques. Le spectre devrait donc présenter une bande de fréquence (ou d'énergie) indéfiniment mince (signal monochromatique). Dans les faits, cette raie a une certaine largeur. Dans le cas d'un gaz, la fonction de Voigt permet de modéliser la largeur de cette raie en raison :
- des collisions entre les molécules (élargissement lorentzien) ;
- de l'effet Doppler-Fizeau dû au mouvement des molécules.
En diffractométrie de rayons X, la fonction de Voigt permet de décrire le profil des pics de diffraction si l'on considère :
- une distribution gaussienne des microcontraintes ;
- un effet de taille de cristallites (loi de Scherrer).
Approximations des fonctions de Voigt
Le produit de convolution n'est pas une opération simple. À l'époque où l'informatique ne permettait pas d'effectuer ce calcul, il a fallu trouver des approximations de cette fonction de Voigt.
Pseudo-fonction de Voigt
Une pseudo-fonction de Voigt (pseudo-Voigt function en anglais) est la somme d'une gaussienne et d'une lorentzienne ayant la même position et la même aire. Le facteur de proportionnalité, noté η, est appelé facteur de Lorentz :
- PV = η·L + (1-η)·G
Pour η = 0, on retrouve une gaussienne et pour η = 1, on retrouve une lorentzienne.
Si l'on compare les pseudo-fonctions de Voigt avec une fonction de Voigt (σ = 1 pour la gaussienne, Γ = 1 pour la lorentzienne), le paramètre de Lorentz donnant l'écart quadratique minimal vaut
- η = 0,834 ± 0,001
Fonction de Pearson VII
où M est le paramètre de forme, ou « largeur de Pearson ».
On écrit parfois une expression simplifiée :
On a
- M < 1 : profil dit 'super lorentzien' ;
- M = 1 : profil de Cauchy : Lorentz (lorentzienne) : Breit-Wigner ;
- M = ∞ : profil de Gauss-Laplace (gaussienne, loi normale).
Cette fonction est utilisée depuis 1977 pour représenter la forme des pics de diffraction X[1].
Annexes
Bibliographie
- M.M. Hall, The Approximation of Symmetric X-Ray Peaks by Pearson Type VII Distributions, J. Apl. Cryst., Vol. 10, 66 (1977).
Articles connexes
- Autres courbes en cloche
- Fonction gaussienne
- Fonction lorentzienne
- Fonction de Pearson
- Fonction maxwellienne
Lien externe
Référence
- ↑ M.M. Hall, The Approximation of Symmetric X-Ray Peaks by Pearson Type VII Distributions, J. Apl. Cryst., Vol. 10, 66 (1977).
- Portail des mathématiques
Catégories : Analyse harmonique | Fonction remarquable
Wikimedia Foundation. 2010.

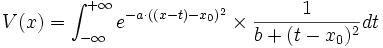
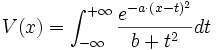


![y = \frac{1}{\left [ 1+ \left (\frac{2(x-x_0) \cdot \sqrt{2^{1/M}-1}}{w} \right )^2 \right ]^M}](/pictures/frwiki/48/0eb3ecc8785f84892590533ca6e0aec7.png)
![y = \left [ 1 + K^2 \frac{(x-x_0)^2}{M} \right ]^{-M}](/pictures/frwiki/51/3792056ad5bd8e871341dc9f69c942f3.png)