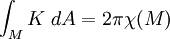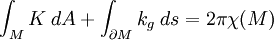Formule De Gauss-Bonnet
- Formule De Gauss-Bonnet
-
Formule de Gauss-Bonnet
En géométrie, la formule de Gauss-Bonnet est une propriété reliant la géométrie et la topologie des surfaces. Elle porte le nom des mathématiciens Carl Friedrich Gauss, qui avait conscience d'une version du théorème, mais ne la publia jamais, et Pierre Ossian Bonnet, qui en publia un cas particulier en 1848.
Énoncé
Soit M une surface compacte (sans bord) ; alors l'intégrale de la courbure de Gauss permet de retrouver la caractéristique d'Euler de la surface
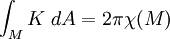
Pour une variété compacte à bord, la formule devient
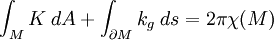
en notant kg la courbure géodésique aux points du bord 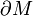 .
.
Si le bord 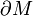 est seulement régulier par morceaux, la formule tient encore en prenant au lieu de l'intégrale
est seulement régulier par morceaux, la formule tient encore en prenant au lieu de l'intégrale 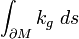 la somme des intégrales correspondantes sur les portions régulières du bord, plus la somme des angles formés aux points anguleux.
la somme des intégrales correspondantes sur les portions régulières du bord, plus la somme des angles formés aux points anguleux.
 Portail de la géométrie
Portail de la géométrie Portail des mathématiques
Portail des mathématiques
Catégories : Surface | Géométrie riemannienne | Carl Friedrich Gauss
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Formule De Gauss-Bonnet de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Formule de gauss-bonnet — En géométrie, la formule de Gauss Bonnet est une propriété reliant la géométrie et la topologie des surfaces. Elle porte le nom des mathématiciens Carl Friedrich Gauss, qui avait conscience d une version du théorème, mais ne la publia jamais, et… … Wikipédia en Français
Formule de Gauss-Bonnet — En géométrie différentielle, la formule de Gauss Bonnet est une propriété reliant la géométrie (au sens de la courbure de Gauss) et la topologie (au sens de la caractéristique d Euler) des surfaces. Elle porte le nom des mathématiciens Carl… … Wikipédia en Français
Gauss (homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Carl Friedrich Gauss (1777 1855), mathématicien, astronome et physicien allemand. Le gauss, une unité de mesure du champ magnétique, noté G. GAUSS, un… … Wikipédia en Français
GAUSS (C. F.) — L’œuvre du mathématicien allemand Carl Friedrich Gauss (né à Brunswick, mort à Göttingen) est un monument d’une ampleur et d’une richesse sans égale: non seulement il y a Gauss mathématicien, mais il y a aussi le calculateur, le géodésien,… … Encyclopédie Universelle
Théorème de Gaus-Bonnet — Formule de Gauss Bonnet En géométrie, la formule de Gauss Bonnet est une propriété reliant la géométrie et la topologie des surfaces. Elle porte le nom des mathématiciens Carl Friedrich Gauss, qui avait conscience d une version du théorème, mais… … Wikipédia en Français
Courbure de Gauss — La courbure de Gauss d une surface paramétrée X en X(P) est le produit des courbures principales. De manière équivalente, la courbure de Gauss est le déterminant de l endomorphisme de Weingarten. Le tableau suivant liste les courbures de Gauss de … Wikipédia en Français
Équations de Gauss-Codazzi — En géométrie riemannienne, les équations de Gauss Codazzi Mainardi sont des équations fondamentales dans le cadre de la théorie des hypersurfaces plongées dans un espace euclidien, et plus généralement des sous variétés d une variété riemannienne … Wikipédia en Français
Méthodes de quadrature de Gauss — Dans le domaine mathématique de l analyse numérique, les méthodes de quadrature sont des approximations de la valeur numérique d une intégrale. En général, on remplace le calcul de l intégrale par une somme pondérée prise en un certain nombre de… … Wikipédia en Français
Pierre-ossian bonnet — Pour les articles homonymes, voir Bonnet. Pierre Ossian Bonnet Pierre Ossian Bonnet, né à Montpellier le … Wikipédia en Français
Pierre Ossian Bonnet — Pour les articles homonymes, voir Bonnet. Pierre Ossian Bonnet Pierre Ossian Bonnet, né à Montpellier le … Wikipédia en Français
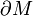 .
.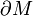 est seulement régulier par morceaux, la formule tient encore en prenant au lieu de l'intégrale
est seulement régulier par morceaux, la formule tient encore en prenant au lieu de l'intégrale 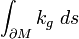 la somme des intégrales correspondantes sur les portions régulières du bord, plus la somme des angles formés aux points anguleux.
la somme des intégrales correspondantes sur les portions régulières du bord, plus la somme des angles formés aux points anguleux.