Courbe du diable
- Courbe du diable
-
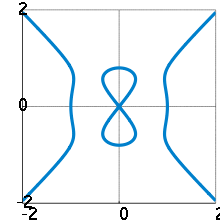
Courbe du diable avec les paramètres a=√10/10 et b=3×a.
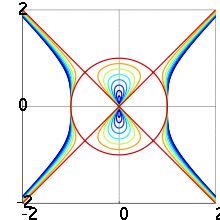
Courbe du diable avec
a allant de 0 à 1 et
b = 1 (la couleur de la courbe allant du bleu au rouge).
La courbe du diable a été étudiée en 1750 par Cramer et en 1810 par Lacroix.
Étymologie
Cette courbe doit son nom à l'arc fermé qui la compose en partie, et qui rappelle la forme d'un jouet populaire à la fin du XVIIIe siècle, le diabolo (en anglais : « the devil on two sticks »).
Équations
- Équation polaire :
 .
.
- Équation cartésienne :

- Autre forme cartésienne :

Voir aussi
Articles connexes
Lien externe
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Courbe du diable de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Courbe Du Diable — avec les paramètres a=√10/10 et b=3×a. La courbe du diable a été étudiée en 1750 par Cramer et en 1810 par Lacroix. Sommaire … Wikipédia en Français
Courbe Brachistochrone — Le mot brachistochrone désigne une courbe dans un plan vertical sur laquelle un point matériel pesant placé dans un champ de pesanteur uniforme, glissant sans frottement et sans vitesse initiale, présente un temps de parcours minimal parmi toutes … Wikipédia en Français
Courbe brachystochrone — Courbe brachistochrone Le mot brachistochrone désigne une courbe dans un plan vertical sur laquelle un point matériel pesant placé dans un champ de pesanteur uniforme, glissant sans frottement et sans vitesse initiale, présente un temps de… … Wikipédia en Français
Courbe — En géométrie, le mot courbe, ou ligne courbe désigne certains sous ensembles du plan, de l espace usuels. Par exemple, les droites, les segments, les lignes polygonales et les cercles sont des courbes. La notion générale de courbe se décline en… … Wikipédia en Français
Courbe brachistochrone — Le mot brachistochrone désigne une courbe dans un plan vertical sur laquelle un point matériel pesant placé dans un champ de pesanteur uniforme, glissant sans frottement et sans vitesse initiale, présente un temps de parcours minimal parmi toutes … Wikipédia en Français
Courbe parabolique — Parabole Pour les articles homonymes, voir Parabole (homonymie). Une parabole La parabole est l intersection d un plan avec un cône … Wikipédia en Français
Courbe Quadrique — Les quadriques sont des courbes du plan exprimés via des polynômes de degré 4. On en distingue plusieurs familles en fonction du genre. Si le genre = 0, alors ce sont les quadriques rationnelles Si le genre = 1, alors ce sont les quadriques… … Wikipédia en Français
Courbe quadrique — Les quadriques sont des courbes du plan exprimés via des polynômes de degré 4. On en distingue plusieurs familles en fonction du genre. Si le genre = 0, alors ce sont les quadriques rationnelles Si le genre = 1, alors ce sont les quadriques… … Wikipédia en Français
Courbe quartique — En géométrie, une courbe quartique est une courbe algébrique de degré quatre. Elle peut être définie par une équation de degré quatre: Ax4 + By4 + Cx3y + Dx2y2 + Exy3 + Fx3 + Gy3 + Hx2y + Ixy2 + Jx2 + Ky2 + Lxy + Mx + Ny + P = 0. Cette équation a … Wikipédia en Français
Deltoide (courbe) — Deltoïde (courbe) La courbe en rouge est une deltoïde. La deltoïde n est autre qu une hypocycloïde à trois rebroussements. Elle fut étudiée pour la première fois par Léonard Euler en 1745. Sommaire 1 Équations cartésiennes … Wikipédia en Français
 .
.



