Courbe quartique
- Courbe quartique
-
En géométrie, une courbe quartique est une courbe algébrique de degré quatre.
Elle peut être définie par une équation de degré quatre:
- Ax4 + By4 + Cx3y + Dx2y2 + Exy3 + Fx3 + Gy3 + Hx2y + Ixy2 + Jx2 + Ky2 + Lxy + Mx + Ny + P = 0.
Cette équation a quinze constantes. Cependant, elle peut être multipliée par une constante non-nulle sans changer la courbe. De ce fait, l'espace des courbes quartiques peut être identifié avec l'espace projectif réel 
. Il en résulte qu'il y a exactement une seule courbe quartique qui passe par un ensemble de quatorze points distincts en position générale, puisque une quartique a 14 degrés de liberté.
Une courbe quartique peut avoir un maximum de:
- Quatre composantes connexes
- Vingt-huit bi-tangentes
- Trois points doubles ordinaires.
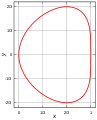
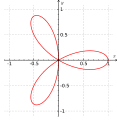
Un exemple de courbe quartique (gauche) est la fenêtre de Viviani.
On distingue plusieurs familles de quartiques en fonction du genre.
- Si le genre = 0, alors ce sont les quartiques rationnelles
- Si le genre = 1, alors ce sont les quartiques elliptiques
- Si le genre = 2, alors ce sont les quartiques du diable
- Si le genre = 3, alors ce sont les quartiques de genre trois
Exemples
-
-
-
-
-
-
-
-
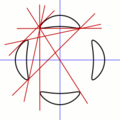
Courbe de Trott et quelques-unes des 28 bi-tangentes.
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Courbe quartique de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Courbe Quartique — En géométrie, une courbe quartique est une courbe algébrique de degré 4. Un exemple de courbe quartique (gauche) est la fenêtre de Viviani. Portail de la géométrie Ce document provient de « Courbe quartique ». Catégorie : Courb … Wikipédia en Français
quartique — ● quartique adjectif (de quart 2) Se dit d une courbe du plan ou d une surface ayant pour équation un polynôme de degré total égal à 4. quartique n. f. GEOM Courbe dont l équation est du quatrième degré. quartique [kaʀtik] n. f. ÉTYM. 1904; de… … Encyclopédie Universelle
Quartique de Klein — La quartique de Klein est le quotient d un pavage uniforme triangulaire d ordre 7. En géométrie hyperbolique, la quartique de Klein, du nom du mathématicien allemand Felix Klein, est une surface de Riemann compacte de genre 3. Elle a le groupe d… … Wikipédia en Français
Quartique rationnelle — Une quartique rationnelle est une courbe définie par un polynôme de degré quatre et de genre zéro. On peut faire la distinction entre : les quartiques rationnelles bicirculaires les quartiques rationnelles non bicirculaires Portail de la… … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
COURBES ALGÉBRIQUES — En fondant la géométrie analytique, Descartes avait substitué au plan de la géométrie d’Euclide l’ensemble R2 des couples de nombres réels et, de ce fait, à la notion de courbe, celle d’équation. La construction d’un point, puis la détermination… … Encyclopédie Universelle
Paradoxe de Cramer — En mathématiques, et plus précisément en géométrie algébrique, le paradoxe de Cramer (nommé d après Gabriel Cramer, mais qui avait déjà été remarqué par Maclaurin) affirme que le nombre de points d intersection de deux courbes de haut degré peut… … Wikipédia en Français
Géométrie différentielle des surfaces — En mathématiques, la géométrie différentielle des surfaces est la branche de la géométrie différentielle qui traite des surfaces (les objets géométriques de l espace usuel E3, ou leur généralisation que sont les variétés de dimension 2), munies… … Wikipédia en Français
Formule de Plücker — En mathématiques, et plus précisément en géométrie algébrique, une formule de Plücker est une relation entre certains invariants numériques de courbes algébriques, tels que le nombre de leurs points critiques, et les invariants correspondants de… … Wikipédia en Français
