650 (nombre)

Nombres 600 à 699

Cet article recense les nombres qui ont des propriétés remarquables allant de 600 à 699.

Sommaire

1 Entiers de 600 à 609
2 Entiers de 610 à 619
3 Entiers de 620 à 629
4 Entiers de 630 à 639
5 Entiers de 640 à 649
6 Entiers de 650 à 659
7 Entiers de 660 à 669
8 Entiers de 670 à 679
9 Entiers de 680 à 689
10 Entiers de 690 à 699

Entiers de 600 à 609

Pour l'année, voir 600

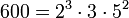
$600 = 2^3 \cdot 3 \cdot 5^2$

un nombre oblong,
un Nombre Harshad.

Pour l'année, voir 601

un nombre premier,
un modèle de voiture, la peugeot 601, produite entre 1934 et 1935,
un nombre pentagonal centré

Pour l'année, voir 602

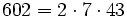$602 = 2 \cdot 7 \cdot 43$ ,

un anti-indicateur,

Pour l'année, voir 603

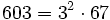$603 = 3^2 \cdot 67$ ,

un nombre Harshad

Pour l'année, voir 604

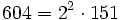$604 = 2^2 \cdot 151$ ,

un anti-indicateur,
un modèle de voiture, la peugeot 604, produite entre 1975 et 1986,

Pour l'année, voir 605

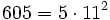$605 = 5 \cdot 11^2$ ,

un nombre Harshad,
un modèle de voiture, la peugeot 605, produite entre 1989 et 1999,

Pour l'année, voir 606

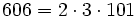$606 = 2 \cdot 3 \cdot 101$ ,

un nombre sphénique,
la somme de six nombres premiers consécutifs (89 + 97 + 101 + 103 + 107 + 109),

Pour l'année, voir 607

un nombre premier,
la somme de trois nombres premiers consécutifs (197 + 199 + 211),
la fonction de Mertens retourne 0 pour ce nombre,
un nombre strictement non-palindrome,
un modèle de voiture, la peugeot 607, produite depuis 1999,
l'indicatif téléphonique d'Ithaca

Pour l'année, voir 608

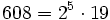$608 =2^5 \cdot 19$ ,

la fonction de Mertens retoure 0 pour ce nombre,
un anti-indicateur

Pour l'année, voir 609

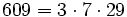$609 =3 \cdot 7 \cdot 29$ ,

un nombre sphénique

Entiers de 610 à 619

Pour l'année, voir 610

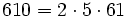$610 = 2 \cdot 5 \cdot 61$ ,

Pour l'année, voir 611

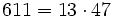
$611 =13 \cdot 47$

Pour l'année, voir 612

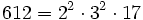$612 = 2^2 \cdot 3^2 \cdot 17$ ,

un nombre Harshad,
un nombre de Zuckerman,
l'indicatif téléphonique de Minneapolis.

Pour l'année, voir 613

un nombre premier,
un nombre carré centré,
le nombre de commandements (mitzvot) dans le judaïsme.
le nombre suspendu au Madison Square Garden en l'honneur des 613 victoires de Red Holzman, l'entraîneur légendaire de l'équipe de basket new-yorkaise, les New York Knicks.
l'indicatif téléphonique de l'Ontario de l'est, au Canada.

Pour l'année, voir 614

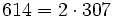$614 = 2 \cdot 307$ ,

un anti-indicateur

Pour l'année, voir 615

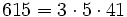$615 = 3 \cdot 5 \cdot 41$ ,

un nombre sphénique

Pour l'année, voir 616

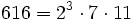$616 = 2^3 \cdot 7 \cdot 11$ ,

une valeur alternative pour le nombre de la Bête (généralement de valeur 666).

Pour l'année, voir 617

un nombre premier,
la somme de cinq nombres premiers consécutifs (109 + 113 + 127 + 131 + 137),
un nombre premier de Chen,
un nombre premier d’Eisenstein sans partie imaginaire

Pour l'année, voir 618

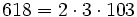$618 = 2 \cdot 3 \cdot 103$ ,

un nombre sphénique

Pour l'année, voir 619

un nombre premier,
un nombre premier strobogrammatique
une factorielle alternative

Entiers de 620 à 629

Pour l'année, voir 620

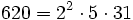$620 = 2^2 \cdot 5 \cdot 31$ ,

la somme de quatre nombres premiers consécutifs (149 + 151 + 157 + 163),
la somme de huit nombres premiers consécutifs (61 + 67 + 71 + 73 + 79 + 83 + 89 + 97)

Pour l'année, voir 621

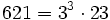$621=3^3 \cdot 23$ ,

un nombre Harshad

Pour l'année, voir 622

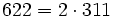$622 = 2 \cdot 311$ ,

un anti-indicateur

Pour l'année, voir 623

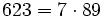
$623 = 7 \cdot 89$

Pour l'année, voir 624

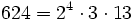$624 = 2^4 \cdot 3 \cdot 13$ ,

la somme des nombres premiers jumeaux (311 + 313),
un nombre Harshad,
un nombre de Zuckerman

Pour l'année, voir 625

$625 = 5 4$

625 = 25²,
la somme de sept nombres premiers consécutifs (73 + 79 + 83 + 89 + 97 + 101 + 103),
un nombre octogonal centré,
un nombre automorphe,
un nombre de Friedman puisque 625= 5^(6-2)

Pour l'année, voir 626

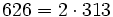$626 = 2 \cdot 313$ ,

un anti-indicateur,
un modèle de voiture, la Mazda 626, la voiture précédant la Mazda 6.
le plus grand nombre de compositions de Wolfgang Amadeus Mozart dans le catalogue de Köchel.
le numéro de l'expérience de Stitch dans le dessin animé "Lilo & Stitch".

Pour l'année, voir 627

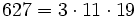$627 = 3 \cdot 11 \cdot 19$ ,

un nombre sphénique,
un nombre de Smith

Pour l'année, voir 628

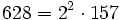$628 = 2^2 \cdot 157$ ,

un anti-indicateur

Pour l'année, voir 629

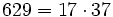$629 = 17 \cdot 37$ ,

un nombre hautement co-indicateur,
un nombre Harshad

Entiers de 630 à 639

Pour l'année, voir 630

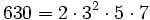$630 = 2 \cdot 3^2 \cdot 5 \cdot 7$ ,

la somme de six nombres premiers consécutifs (97 + 101 + 103 + 107 + 109 + 113),
un nombre triangulaire,
un nombre hexagonal,
un nombre Harshad

Pour l'année, voir 631

Pour l'année, voir 632

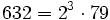
$632 =2^3 \cdot 79$

Pour l'année, voir 633

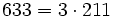$633 =3 \cdot 211$ ,

la somme de trois nombres premiers consécutifs (199 + 211 + 223),
une partie du titre du film 633 Squadron

Pour l'année, voir 634

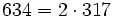$634 =2 \cdot 317$ ,

un anti-indicateur,
un nombre de Smith

Pour l'année, voir 635

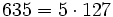$635 =5 \cdot 127$ ,

la somme de neuf nombres premiers consécutifs (53 + 59 + 61 + 67 + 71 + 73 + 79 + 83 + 89),
la fonction de Mertens retourne 0 pour ce nombre.

Pour l'année, voir 636

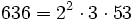$636 =2^2 \cdot 3 \cdot 53$ ,

la somme de dix nombres premiers consécutifs (43 + 47 + 53 + 59 + 61 + 67 + 71 + 73 + 79 + 83),
un nombre de Smith,
la fonction de Mertens retourne 0 pour ce nombre,

Pour l'année, voir 637

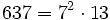$637 =7^2 \cdot 13$ ,

la fonction de Mertens retourne 0 pour ce nombre,
un nombre décagonal.

Pour l'année, voir 638

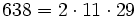$638 =2 \cdot 11 \cdot 29$ ,

un nombre sphénique,
la somme de quatre nombres premiers consécutifs (151 + 157 + 163 + 167),
un anti-indicateur,
un nombre heptagonal centré

Pour l'année, voir 639

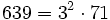$639 = 3^2 \cdot 71$ ,

la somme des vingt premiers nombres premiers,
le code de la norme ISO pour la représentation des langues.

Entiers de 640 à 649

Pour l'année, voir 640

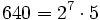$640=2^7 \cdot 5$ ,

un nombre de Harshad

Pour l'année, voir 641

un nombre premier,
un nombre premier de Sophie Germain,
un facteur du 4294967297 (le plus petit nombre de Fermat non premier),
un nombre premier de Chen,
un nombre premier d’Eisenstein sans partie imaginaire

Pour l'année, voir 642

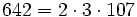$642=2 \cdot 3 \cdot 107$ ,

un nombre sphénique

Pour l'année, voir 643

un nombre premier,
le plus grand facteur premier de 123456

Pour l'année, voir 644

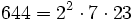$644=2^2 \cdot 7 \cdot 23$ ,

un anti-indicateur,
un nombre Harshad

Pour l'année, voir 645

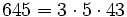$645 =3 \cdot 5 \cdot 43$ ,

Pour l'année, voir 646

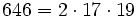$646 =2 \cdot 17 \cdot 19$ ,

un nombre sphénique,
une partie du nom de la norme ISO 646, la norme internationale pour la variante 7-bit du code ASCII.

Pour l'année, voir 647

un nombre premier,
la somme de cinq nombres premiers consécutifs (113 + 127 + 131 + 137 + 139),
un nombre premier de Chen,
un nombre premier d’Eisenstein sans partie imaginaire

Pour l'année, voir 648

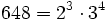$648 =2^3 \cdot 3^4$ ,

un nombre de Harshad

Pour l'année, voir 649

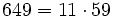$649 =11 \cdot 59$ ,

un nombre de Smith

Entiers de 650 à 659

Pour l'année, voir 650

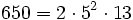$650 =2 \cdot 5^2 \cdot 13$ ,

Pour l'année, voir 651

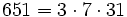$651=3 \cdot 7 \cdot 31$ ,

un nombre sphénique,
un nombre ennéagonal

Pour l'année, voir 652

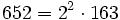
$652=2^2 \cdot 163$

Pour l'année, voir 653

un nombre premier,
un nombre premier de Sophie Germain,
un nombre premier de Chen,
un nombre premier d’Eisenstein sans partie imaginaire

Pour l'année, voir 654

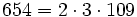$654 =2 \cdot 3 \cdot 109$ ,

Pour l'année, voir 655

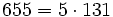
$655 =5 \cdot 131$

Pour l'année, voir 656

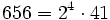
$656=2^4 \cdot 41$

Pour l'année, voir 657

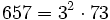
$657=3^2 \cdot 73$

Pour l'année, voir 658

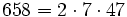$658=2 \cdot 7 \cdot 47$ ,

un nombre sphénique

Pour l'année, voir 659

un nombre premier,
un nombre premier de Sophie Germain,
un somme de sept nombres premiers consécutifs (79 + 83 + 89 + 97 + 101 + 103 + 107),
un nombre premier de Chen,
la fonction de Mertens atteint un nouveau niveau -10 qui reste jusqu'à 661,
un nombre hautement co-indicateur,
un nombre premier d’Eisenstein sans partie imaginaire,
un nombre strictement non-palindrome

Entiers de 660 à 669

Pour l'année, voir 660

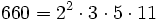$660=2^2 \cdot 3 \cdot 5 \cdot 11$ ,

la somme de quatre nombres premiers consécutifs (157 + 163 + 167 + 173),
la somme de six nombres premiers consécutifs (101 + 103 + 107 + 109 + 113 + 127),
la somme de huit nombres premiers consécutifs (67 + 71 + 73 + 79 + 83 + 89 + 97 + 101),
un nombre Harshad

Pour l'année, voir 661

un nombre premier,
la somme de trois nombres premiers consécutifs (211 + 223 + 227),
la fonction de Mertens atteint un nouveau niveau -11 qui reste jusqu'au nombre 665,
un nombre étoilé

Pour l'année, voir 662

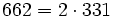$662=2 \cdot 331$ ,

un anti-indicateur

Pour l'année, voir 663

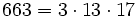$663 =3 \cdot 13 \cdot 17$ ,

un nombre sphénique,
un nombre de Smith

Pour l'année, voir 664

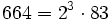
$664 =2^3 \cdot 83$

Pour l'année, voir 665

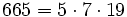$665=5 \cdot 7 \cdot 19$ ,

un nombre sphénique,
la fonction de Mertens atteint un nouveau niveau -12 qui reste jusqu'au nombre 1105

Pour l'année, voir 666

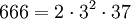
$666=2 \cdot 3^2 \cdot 37$

un nombre abondant.
Puisque 36 est un carré et un nombre triangulaire, 666 est le sixième nombre de la forme $n 2 (n 2 + 1) / 2$ (carrés triangulaires) et le huitième nombre de la forme $n (n + 1)(n 2 + n + 2) / 8$ (nombres doublement triangulaires).
le rapport harmonique des chiffres décimaux de 666 est un nombre entier : 3/(1/6 + 1/6 + 1/6) = 6, faisant de 666 le 54^e nombre avec cette propriété.
un nombre palindrome en base 10,
un nombre uniforme,
un nombre de Smith.
un carré magique à inverse premier basé sur 1/149 en base 10 possède un total magique de 666.
un membre des indices de nombre premier dans la suite de Padovan, 3, 4, 5, 7, 8, 14, 19, 30, 37, 84, 128, 469, 666, 1262, 1573, 2003, 2210, (sont les premiers de ceux-ci).
Padovan sequence (sequence A112882) sur OEIS.
la somme de presque tous les chiffres romains (excepté M), du plus petit au plus grand, I + V + X + L + C + D ou du plus grand au plus petit, D + C + L + X + V + I est égale à 666,
(1 + 5 + 10 + 50 + 100 + 500 = 666),
la somme de tous les nombres de 1 à 36 (1 + 2 + 3 + ... + 35 + 36) donne 666, ce qui en fait un nombre triangulaire. On peut donc écrire que
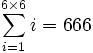: $\sum_{i=1}^{6\times6} i = 666$ ,
en remarquant que 36 est la somme des nombres de 1 à 8,

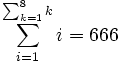$\sum_{i=1}^{\sum_{k=1}^8 k} i = 666$ ;
la somme des positions dans l'alphabet, multipliée par 9, de chacun des chiffres romains (I, V, X, L, C et D) qui le composent :
81 + 198 + 216 + 27 + 108 + 36 = 666
(I, neuvième lettre, donne 9 * 9 = 81; V, vingt-deuxième lettre, donne 22 * 9 = 198...),
Une autre manière de calculer est de poser le calcul suivant, où on retrouve quatre fois le nombre 666 :

(6 x 6 x 6) + (6 x 6 x 6) + (6 x 6 x 6) + (6 + 6 + 6) = 666,
De plus, on peut remarquer, que la somme des carrés des nombres premiers jusqu'à 17 donne 666. Ainsi :

2² + 3² + 5² + 7² + 11² + 13² + 17² = 666.
nommé le Nombre de la bête, jusqu'en 2004 où une équipe de chercheurs ont identifié le chiffre 666 comme étant le nom chiffré de l'empereur Néron. Les hébreux se donnaient des chiffres et des nombres à la place des noms (voir documentaire BBC). Ainsi Saint Jean pouvait échapper, comme les autres, à toutes représailles. 666 n'a jamais été le nombre de la bête, encore moins celui d'un quelconque 'diable'. Mais la légende persistera toujours.
Puisque le "sinus du diable" 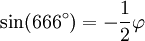$\sin (666^\circ) = - \frac{1}{2} \varphi$ , où φ est le nombre d'or, cette expression a été paraphrasée par la raillerie humoristique "Le signe du diable est l'opposé du bien, mais seulement à moitié comme fort". Noter que (sin 306°) et (sin -54°) sont mathématiquement synonymes avec (sin 666°).
Vicarius Filii Dei, une épithète latine pour le pape qui signifie littéralement "vicaire du fils de Dieu", en prenant les valeurs des lettres des chiffres romains donnent 666 (ce qui donnerait VICIVILIIDI). Cette épithète ne fut jamais utilisée par l'église catholique elle-même et fut probablement inventée par une personne qui croyait que l'Antichrist serait un pape.
utilisé comme un surnom par Aleister Crowley, un occultiste qui s'est dénommé comme la bête dont il est fait mention dans le Livre des Révélations.
Les codes-barre trouvés sur la plupart des produits commerciaux sont caractérisés par des barres de garde au début, au milieu et à la fin faites par deux lignes fines. Deux lignes fines signifie dans l'encodage UPC le chiffre 6 (et pas d'autre chiffre), et donc, pour l'œil humain (mais pas pour le lecteur électronique de code-barre), les barres de garde apparaissent comme le nombre 666. Certaines personnes interpretent ceci comme une réalisation de la prophétie citée dans le Livre des Révélations : "Sans ce nombre, un individu ne sera pas capable d'acheter ou de vendre. [1]
Le remake du film d'horreur de 2006 The Omen fut réalisé le 6 juin 2006 (06/06/06) à 06:06:06 le matin.
le n° de port utilisé par le jeu Doom lorsque l'on joue contre un autre joueur via TCP.
La plupart des versions du jeu vidéo Lemmings comporte un niveau appelé "Tous les 6...". Le niveau comportant trois 6 a été construit sur un terrain de lave "infernal", 66 Lemmings et 66 de chaque sorte, un temps limite de 6 minutes, un taux de rejets de 66 et le joueur doit sauver 66 % des Lemmings.
Dans la culture chinoise, 666 sonne beaucoup comme les mots 'Choses allant sans-à coup'. Il est considéré comme un des nombres les plus chanceux. Il peut être vu en évidence dans beaucoup de magasins à travers le pays, et les gens sont prêts à payer un supplément pour obtenir un téléphone portable incluant cette suite de chiffres.
6-6-6 est Waw-Waw-Waw ("WWW") en hébreu, les lettres ont des valeurs numériques. Le nombre 666, néanmoins est Taw-Resch-Samech-Waw (400-200-60-6), puisqu'en hébreu, les centaines, les dizaines et les unités ont des caractères différents.
la quantité de talents d'or que le roi Salomon collecta en une année.
le nombre des descendants d'Adonikam qui retournèrent à Jérusalem après l'exil de Babylone.
le nom original du virus informatique du Macintosh SevenDust qui fut découvert en 1998.
Six-Sixty-Six est le titre d'une chanson de rock Larry Norman. Une version a été enregistrée par Frank Black et les catholiques.
le surnom du groupe punk rock canadien Kill Cheerleader.

Pour l'année, voir 667

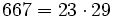
$667=23 \cdot 29$

Pour l'année, voir 668

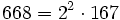$668 =2^2 \cdot 167$ ,

un anti-indicateur

Pour l'année, voir 669

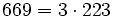
$669=3 \cdot 223$

Entiers de 670 à 679

Pour l'année, voir 670

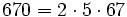$670=2 \cdot 5 \cdot 67$ ,

Pour l'année, voir 671

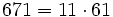
$671=11 \cdot 61$

Le nombre de solutions pour le Problème des huit dames pour n = 11.

Pour l'année, voir 672

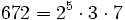$672 =2^5 \cdot 3 \cdot 7$ ,

un nombre en division harmonique

Pour l'année, voir 673

un nombre premier

Pour l'année, voir 674

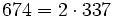$674 =2 \cdot 337$ ,

un anti-indicateur

Pour l'année, voir 675

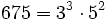
$675 =3^3 \cdot 5^2$

Pour l'année, voir 676

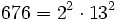
$676=2^2 \cdot 13^2$

676 = 26²

Pour l'année, voir 677

un nombre premier,
un nombre premier de Chen,
un nombre premier d’Eisenstein sans partie imaginaire

Pour l'année, voir 678

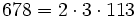$678 = 2 \cdot 3 \cdot 113$ ,

un nombre sphénique,
un anti-indicateur

Pour l'année, voir 679

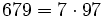$679 = 7 \cdot 97$ ,

la somme de trois nombres premiers consécutifs (223 + 227 + 229),
la somme de neuf nombres premiers consécutifs (59 + 61 + 67 + 71 + 73 + 79 + 83 + 89 + 97)

Entiers de 680 à 689

Pour l'année, voir 680

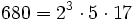$680=2^3 \cdot 5 \cdot 17$ ,

un nombre tétraédrique,
un anti-indicateur

Pour l'année, voir 681

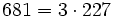$681=3 \cdot 227$ ,

un nombre pentagonal centré

Pour l'année, voir 682

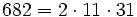$682=2 \cdot 11 \cdot 31$ ,

un nombre sphénique,
la somme de quatre nombres premiers consécutifs (163 + 167 + 173 + 179),
la somme de dix nombres premiers consécutifs (47 + 53 + 59 + 61 + 67 + 71 + 73 + 79 + 83 + 89)

Pour l'année, voir 683

un nombre premier,
un nombre premier de Sophie Germain,
la somme de cinq nombres premiers consécutifs (127 + 131 + 137 + 139 + 149),
un nombre premier de Chen,
un nombre premier d’Eisenstein sans partie imaginaire

Pour l'année, voir 684

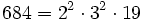$684=2^2 \cdot 3^2 \cdot 19$ ,

un nombre Harshad

Pour l'année, voir 685

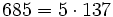$685=5 \cdot 137$ ,

un nombre carré centré

Pour l'année, voir 686

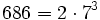$686=2 \cdot 7^3$ ,

un anti-indicateur

Pour l'année, voir 687

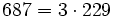$687=3 \cdot 229$ .

le numéro de coffre de la famille Potter à la banque Gringotts Bank, dans le film Harry Potter.

Pour l'année, voir 688

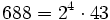$688 =2^4 \cdot 43$ ,

un nombre de Friedman puisque </math>688 = 8 \cdot 86</math>

Pour l'année, voir 689

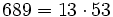$689 =13 \cdot 53$ ,

la somme de trois nombres premiers consécutifs (227 + 229 + 233),
la somme de sept nombres premiers consécutifs (83 + 89 + 97 + 101 + 103 + 107 + 109)

Entiers de 690 à 699

Pour l'année, voir 690

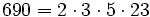$690=2 \cdot 3 \cdot 5 \cdot 23$ ,

la somme de six nombres premiers consécutifs (103 + 107 + 109 + 113 + 127 + 131),
un nombre de Smith,
un nombre Harshad,
une partie du nom de la norme ISO 690 pour les références bibliographiques

Pour l'année, voir 691

un nombre premier,
le numérateur (négatif) du nombre de Bernoulli B₁₂=-691/2730.
la fonction tau de Ramanujan τ et la fonction diviseur σ₁₁ sont reliées par la congruence remarquable 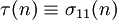$\tau(n) \equiv \sigma_{11}(n)\,$ (mod 691).

Pour l'année, voir 692

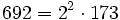
$692=2^2 \cdot 173$

Pour l'année, voir 693

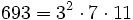
$693 =3^2 \cdot 7 \cdot 11$

Pour l'année, voir 694

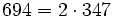$694=2 \cdot 347$ ,

un nombre triangulaire centré,
un anti-indicateur

Pour l'année, voir 695

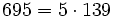
$695=5 \cdot 139$

Pour l'année, voir 696

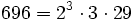$696=2^3 \cdot 3 \cdot 29$ ,

la somme de huit nombres premiers consécutifs (71 + 73 + 79 + 83 + 89 + 97 + 101 + 103)

Pour l'année, voir 697

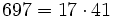
$697 =17 \cdot 41$

Pour l'année, voir 698

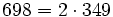$698=2 \cdot 349$ ,

un anti-indicateur

Pour l'année, voir 699

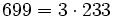
$699 =3 \cdot 233$

Liste des nombres
← 600 · 601 · 602 · 603 · 604 · 605 · 606 · 607 · 608 · 609 · →
← 600 · 610 · 620 · 630 · 640 · 650 · 660 · 670 · 680 · 690 · →
← 0 · 100 · 200 · 300 · 400 · 500 · 600 · 700 · 800 · 900 · →

Portail des mathématiques

Ce document provient de « Nombres 600 %C3%A0 699 ».

Catégorie : Nombre entier

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article 650 (nombre) de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

Nombre Oblong — Un nombre oblong, ou nombre pronique ou nombre hétéromécique, est un nombre qui est le produit de deux entiers naturels consécutifs, c’est à dire, n(n + 1). Chaque nombre oblong pour n est aussi le double du nombre triangulaire pour n. Les… … Wikipédia en Français
Nombre Pyramidal Carré — Representation graphique du nombre pyramidal carré 30 = 1²+2²+3²+4² = 1+4+9+16. Un nombre pyramidal carré est un nombre figuré qui représente une pyramide avec une base et quatre côtés. Le nième nombre pyramidal carré est … Wikipédia en Français
Nombre carré pyramidal — Nombre pyramidal carré Representation graphique du nombre pyramidal carré 30 = 1²+2²+3²+4² = 1+4+9+16. Un nombre pyramidal carré est un nombre figuré qui représente une pyramide avec une base et quatre côtés. Le nième nombre… … Wikipédia en Français
Nombre pyramidal carre — Nombre pyramidal carré Representation graphique du nombre pyramidal carré 30 = 1²+2²+3²+4² = 1+4+9+16. Un nombre pyramidal carré est un nombre figuré qui représente une pyramide avec une base et quatre côtés. Le nième nombre… … Wikipédia en Français
(650) Amalasuntha — Descubrimiento Descubridor August Kopff Fecha 4 de octubre de 1907 Nombre Provisional 1907 AM … Wikipedia Español
Nombre oblong — Un nombre oblong, ou nombre pronique ou nombre hétéromécique, est un nombre qui est le produit de deux entiers naturels consécutifs, c’est à dire, n(n + 1). Chaque nombre oblong pour n est aussi le double du nombre triangulaire pour n. Les… … Wikipédia en Français
Nombre guide — Flash photographique Pour les articles homonymes, voir Flash … Wikipédia en Français
Nombre de parlementaires sous la Cinquième République — Le nombre de parlementaires, députés et sénateurs, siégeant respectivement à l Assemblée nationale et au Sénat, a évolué au cours de la Cinquième République française. La constitution de 1958, dans son article 25, renvoie à la loi organique et à… … Wikipédia en Français
Nombre pyramidal carré — Representation graphique du nombre pyramidal carré 30 = 1²+2²+3²+4² = 1+4+9+16. Un nombre pyramidal carré est un nombre figuré qui représente une pyramide avec une base et quatre côtés. Le nième nombre pyramidal carré est … Wikipédia en Français
Nombre premier primoriel — Un nombre premier primoriel est un nombre premier de la forme P(p) + 1 ou P(p) 1, où p est lui même premier et P(p) est la primorielle associée. Exemples On trouvera dans la table suivante les douze plus petits nombres premiers primoriels. p P(p) … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

650 (nombre)

Nombres 600 à 699

Sommaire

Entiers de 600 à 609

Entiers de 610 à 619

Entiers de 620 à 629

Entiers de 630 à 639

Entiers de 640 à 649

Entiers de 650 à 659

Entiers de 660 à 669

Entiers de 670 à 679

Entiers de 680 à 689

Entiers de 690 à 699

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

650 (nombre)

Nombres 600 à 699

Sommaire

Entiers de 600 à 609

Entiers de 610 à 619

Entiers de 620 à 629

Entiers de 630 à 639

Entiers de 640 à 649

Entiers de 650 à 659

Entiers de 660 à 669

Entiers de 670 à 679

Entiers de 680 à 689

Entiers de 690 à 699

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link