- Nombre Palindrome
-
Nombre palindrome
Un nombre palindrome est un nombre symétrique écrit dans une certaine base a comme ceci :
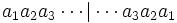 .
.Tous les nombres en base 10 d'un chiffre {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} sont palindromes. Il existe neuf nombres palindromes à deux chiffres :
Il existe 90 nombres palindromes de trois chiffres :
- {101, 111, 121, 131, 141, 151, 161, 171, 181, 191, ..., 909, 919, 929, 939, 949, 959, 969, 979, 989, 999} et aussi 90 nombres palindromes de quatre chiffres :
- {1001, 1111, 1221, 1331, 1441, 1551, 1661, 1771, 1881, 1991, ..., 9009, 9119, 9229, 9339, 9449, 9559, 9669, 9779, 9889, 9999},
donc, il existe 199 nombres palindromes inférieurs à 104. Il existe 1 099 nombres palindromes inférieurs à 105 et pour les autres exposants de 10n, nous avons : 1 999,10 999,19 999,109 999,199 999,1 099 999, ... Encyclopédie électronique des suites entières (id=A070199). Pour certains types de nombres palindromes, ces valeurs sont indiquées dans la table ci-dessous. Ici, 0 est inclus.
101 102 103 104 105 106 107 108 109 1010 n naturel 9 90 199 1099 1999 10999 19999 109999 199999 n pair 5 9 49 89 489 + + + + + n impair 5 10 60 110 610 + + + + + n carré parfait 3 6 13 14 19 + + n premier 4 5 20 113 781 5953 n sans carré 6 12 67 120 675 + + + + + n avec carré (μ(n)=0) 3 6 41 78 423 + + + + + n carré avec racine première 2 3 5 n avec un nombre pair de facteurs premiers distincts (μ(n)=1) 2 6 35 56 324 + + + + + n avec un nombre impair de facteurs premiers distincts (μ(n)=-1) 5 7 33 65 352 + + + + + n pair avec un nombre impair de facteurs premiers n pair avec un nombre impair de facteurs premiers distincts 1 2 9 21 100 + + + + + n impair avec un nombre impair de facteurs premiers 0 1 12 37 204 + + + + + n impair avec un nombre impair de facteurs premiers distincts 0 0 4 24 139 + + + + + n pair sans-carré avec un nombre pair de facteurs premiers distincts 1 2 11 15 98 + + + + + n impair sans-carré avec un nombre pair de facteurs premiers distincts 1 4 24 41 226 + + + + + n impair avec exactement deux facteurs premiers 1 4 25 39 205 + + + + + n pair avec exactement deux facteurs premiers 2 3 11 64 + + + + + n pair avec exactement trois facteurs premiers 1 3 14 24 122 + + + + + n pair avec exactement trois facteurs premiers distincts n impair avec exactement trois facteurs premiers 0 1 12 34 173 + + + + + n nombre de Carmichaël 0 0 0 0 0 1+ + + + + n pour lequel σ(n) est palindrome 6 10 47 114 688 + + + + + en ajouter plus Buckminster Fuller a qualifié les nombres palindromes nombres de Schéhérazade dans son livre « Synergetics », puisque Schéhérazade était le nom de la femme qui narrait les « 1001 nuits ».
Des additions ayant un palindrome pour résultat
Prenez un nombre au hasard. Additionnez-le avec son inverse en lecture. Selon le nombre, vous devrez procéder à une ou plusieurs additions successives du même type, mais à un certain moment, le résultat de l'addition donnera toujours un palindrome.
1234 + 4321 = 5555, c'est un palindrome. Autre exemple plus classique : 149 + 941 = 1090; 1090 + 0901 = 1991 vous obtenez un palindrome
Pourquoi ? Nul ne le sait et les mathématiciens cherchent encore le nombre dont la ou les additions ne donneraient pas de palindrome. Ceux-ci sont appelé Nombre de Lychrel.
On peut considérer cette découverte comme une invention de l'homme à la seule exception que les mathématiques détiennent un secret que nous ignorons tous !
Voir aussi
- Portail des mathématiques
Catégorie : Propriété décimale
Wikimedia Foundation. 2010.
