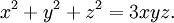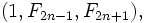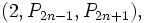Nombre De Markov

Nombre De Markov

Nombre de Markov

En mathématiques, un nombre de Markov ou nombre de Markoff est un nombre entier positif x, y ou z qui est une partie d'une solution de l'équation diophantienne de Markov

x^2 + y^2 + z^2 = 3xyz.\,

Les premiers nombres de Markov sont

1, 2, 5, 13, 29, 34, 89, 169, 194, 233, 433, 610, 985, 1325, ... suite A002559 de l’OEIS

apparaissant comme les coordonnées de triplets de Markov

(1, 1, 1), (1, 1, 2), (1, 2, 5), (1, 5, 13), (2, 5, 29), (1, 13, 34), (1, 34, 89), (2, 29, 169), (5, 13, 194), (1, 89, 233), (5, 29, 433), (89, 233, 610), etc.
Les nombres de Markov, disposés dans un arbre binaire.

Il existe une infinité de nombres de Markov et de triplets de Markov. La symétrie de l'équation de Markov nous permet de réarranger l'ordre des coordonnées, donc un triplet de Markov (a,b,c) peut être normalisé, comme ci-dessus, en supposant que 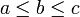a\le b\le c. À côté des deux plus petits triplets, chaque triplet de Markov (a,b,c) est constitué de trois entiers distincts. La Conjecture de l'Unicité établit que pour un nombre de Markov donné c, il existe exactement une solution normalisée ayant c comme son plus grand élément. (A030452 liste les nombres de Markov qui apparaissent dans les solutions où un des deux autres termes est 5).

En 1979, Don B. Zagier démontra que le nième nombre de Markov est asymptotiquement donné par

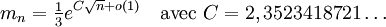m_n = \tfrac13 e^{C\sqrt{n}+o(1)} \quad\text{avec } C=2,3523418721\ldots.

De plus, il mis en évidence que x2 + y2 + z2 = 3xyz + 4 / 9, une approximation extrêmement bonne de l'équation diophantienne originale, est équivalent à f(x) + f(y) = f(z) avec f(t) = arcosh(3t/2).[1]

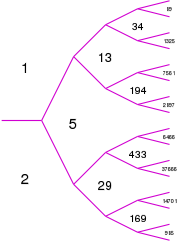
Les nombres de Markov peuvent aussi être disposés dans un arbre binaire. Le plus grand nombre d'un niveau quelconque est toujours le troisième à partir du bas. Tous les nombres de Markov d'une région adjacente à la région de 2 sont indexés par des nombres de Pell impairs (ou des nombres n tels que 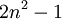2n^2 - 1\, est un carré, A001653), et tous les nombres de Markov sur les régions adjacentes à 1 sont indexés par des nombres de Fibonacci (A001519). Ainsi, il existe une infinité de triplets de Markov de la forme

(1, F_{2n - 1}, F_{2n + 1}),\,

where Fx is the xth Fibonacci number. Likewise, there are infinitely many Markov triples of the form

(2, P_{2n - 1}, P_{2n + 1}),\,

où Px est le xième nombre de Pell.

Connaissant un triplet de Markov (x, y, z), on peut trouver un autre triplet de Markov, de la forme (x,y,3xy − z). Les nombres de Markov ne sont pas toujours premiers; mais les membres d'un triplet de Markov sont toujours premiers entre eux. Il n'est pas nécessaire que x < y < z soit dans l'ordre pour le triplet (x,y,3xy − z) fournisse un autre triplet. En fait, si on ne change pas l'ordre des membres avant d'appliquer de nouveau la transformation, il retourne le même triplet avec lequel on est parti. Ainsi, en commençant avec (1, 1, 2) et en échangeant y et z avant chaque itération de la transformation liste les triplets de Markov avec les nombres de Fibonacci. En commençant avec le même triplet et en échangeant x et z avant chaque itération donne les triplets avec les nombres de Pell.

Le nième nombre de Lagrange peut être calculé à partir du nième nombre Markov avec la formule

L_n = \sqrt{9 - {4 \over {m_n}^2}}.\,

Les nombres de Markov ont été nommés en l'honneur du mathématicien russe Andrei Markov.

Notes et références

  1. ↑ Don B. Zagier, "On the Number of Markoff Numbers Below a Given Bound", Mathematics of Computation, vol.39, no. 160 (1982), p. 709–723.
Ce document provient de « Nombre de Markov ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Nombre De Markov de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Nombre de markov — En mathématiques, un nombre de Markov ou nombre de Markoff est un nombre entier positif x, y ou z qui est une partie d une solution de l équation diophantienne de Markov Les premiers nombres de Markov sont 1, 2, 5, 13, 29, 34, 89, 169, 194, 233,… …   Wikipédia en Français

  • Nombre de Markov — En mathématiques, un nombre de Markov ou nombre de Markoff est un nombre entier positif x, y ou z qui est une partie d une solution de l équation diophantienne de Markov Les premiers nombres de Markov sont 1, 2, 5, 13, 29, 34, 89, 169, 194, 233,… …   Wikipédia en Français

  • 1500 (nombre) — Nombres 1000 à 1999 Cet article recense la plupart des nombres qui ont des propriétés remarquables allant de mille (1000) à mille neuf cent quatre vingt dix neuf (1999). Article détaillé : 1000 (nombre). Sommaire 1 Nombres dans le 1er… …   Wikipédia en Français

  • 1988 (nombre) — Nombres 1000 à 1999 Cet article recense la plupart des nombres qui ont des propriétés remarquables allant de mille (1000) à mille neuf cent quatre vingt dix neuf (1999). Article détaillé : 1000 (nombre). Sommaire 1 Nombres dans le 1er… …   Wikipédia en Français

  • 400 (nombre) — Nombres 400 à 499 Cet article recense les nombres qui ont des propriétés remarquables allant de quatre cents (400) à quatre cent quatre vingt dix neuf (499). Sommaire 1 Entiers de 400 à 409 2 Entiers de 410 à 419 3 Entiers de 420 à 429 …   Wikipédia en Français

  • 400 à 499 (nombre) — Nombres 400 à 499 Cet article recense les nombres qui ont des propriétés remarquables allant de quatre cents (400) à quatre cent quatre vingt dix neuf (499). Sommaire 1 Entiers de 400 à 409 2 Entiers de 410 à 419 3 Entiers de 420 à 429 …   Wikipédia en Français

  • 401 (nombre) — Nombres 400 à 499 Cet article recense les nombres qui ont des propriétés remarquables allant de quatre cents (400) à quatre cent quatre vingt dix neuf (499). Sommaire 1 Entiers de 400 à 409 2 Entiers de 410 à 419 3 Entiers de 420 à 429 …   Wikipédia en Français

  • 450 (nombre) — Nombres 400 à 499 Cet article recense les nombres qui ont des propriétés remarquables allant de quatre cents (400) à quatre cent quatre vingt dix neuf (499). Sommaire 1 Entiers de 400 à 409 2 Entiers de 410 à 419 3 Entiers de 420 à 429 …   Wikipédia en Français

  • 600 (nombre) — Nombres 600 à 699 Cet article recense les nombres qui ont des propriétés remarquables allant de 600 à 699. Sommaire 1 Entiers de 600 à 609 2 Entiers de 610 à 619 3 Entiers de 620 à 629 4 Enti …   Wikipédia en Français

  • 610 (nombre) — Nombres 600 à 699 Cet article recense les nombres qui ont des propriétés remarquables allant de 600 à 699. Sommaire 1 Entiers de 600 à 609 2 Entiers de 610 à 619 3 Entiers de 620 à 629 4 Enti …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”