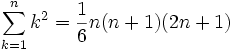Nombre Pyramidal Carré

Nombre pyramidal carré

Representation graphique du nombre pyramidal carré 30 = 1²+2²+3²+4² = 1+4+9+16.

Un nombre pyramidal carré est un nombre figuré qui représente une pyramide avec une base et quatre côtés. Le nième nombre pyramidal carré est

$\sum_{k=1}^nk^2={1 \over 6}n(n + 1)(2n + 1)$

Les premiers petits nombres pyramidaux carrés sont :

1, 5, 14, 30, 55, 91, 140, 204, 285, 385, 506, 650, 819

Les nombres pyramidaux carrés peuvent être modélisés dans l'espace physique avec un nombre donné de balles et une forme carrée qui maintient le carré de balles formant la base, c’est-à-dire n². Excepté 1, il existe seulement un autre nombre qui est à la fois carré et pyramidal carré, 4900. Ce résultat fut prouvé par G.N. Watson en 1918.

La somme de deux nombres pyramidaux carrés consécutifs forme un nombre octaédrique.

Voir aussi

Nombre tétraédrique

Portail des mathématiques

Ce document provient de « Nombre pyramidal carr%C3%A9 ».

Catégories : Nombre figuré | Pyramide

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Nombre Pyramidal Carré de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Nombre pyramidal carre — Nombre pyramidal carré Representation graphique du nombre pyramidal carré 30 = 1²+2²+3²+4² = 1+4+9+16. Un nombre pyramidal carré est un nombre figuré qui représente une pyramide avec une base et quatre côtés. Le nième nombre… … Wikipédia en Français
Nombre pyramidal carré — Representation graphique du nombre pyramidal carré 30 = 1²+2²+3²+4² = 1+4+9+16. Un nombre pyramidal carré est un nombre figuré qui représente une pyramide avec une base et quatre côtés. Le nième nombre pyramidal carré est … Wikipédia en Français
Nombre Pyramidal — Un nombre pyramidal est un nombre figuré qui représente une pyramide, comme par exemple les piles de boulets de canon. Leur expression est réalisée à partir des nombres polygonaux, en les sommant, de 1 jusqu à un certain rang. Puisqu il existe… … Wikipédia en Français
Nombre Pyramidal Pentagonal — Un nombre pyramidal pentagonal est un nombre égal à la somme des premiers nombres pentagonaux. Les premiers nombres pyramidaux pentagonaux sont : 1, 6, 18, 40, 75, 126, 196, 288, 405, 550, 726, 936, 1183, 1470, 1800, 2176, 2601, 3078, 3610,… … Wikipédia en Français
Nombre pyramidal — Un nombre pyramidal est un nombre figuré qui représente une pyramide, comme par exemple les piles de boulets de canon. Leur expression est réalisée à partir des nombres polygonaux, en les sommant, de 1 jusqu à un certain rang. Puisqu il existe… … Wikipédia en Français
Nombre pyramidal pentagonal — Un nombre pyramidal pentagonal est un nombre égal à la somme des premiers nombres pentagonaux. Les premiers nombres pyramidaux pentagonaux sont : 1, 6, 18, 40, 75, 126, 196, 288, 405, 550, 726, 936, 1183, 1470, 1800, 2176, 2601, 3078, 3610,… … Wikipédia en Français
Nombre carré pyramidal — Nombre pyramidal carré Representation graphique du nombre pyramidal carré 30 = 1²+2²+3²+4² = 1+4+9+16. Un nombre pyramidal carré est un nombre figuré qui représente une pyramide avec une base et quatre côtés. Le nième nombre… … Wikipédia en Français
Nombre pentagonal pyramidal — Nombre pyramidal pentagonal Un nombre pyramidal pentagonal est un nombre égal à la somme des premiers nombres pentagonaux. Les premiers nombres pyramidaux pentagonaux sont : 1, 6, 18, 40, 75, 126, 196, 288, 405, 550, 726, 936, 1183, 1470,… … Wikipédia en Français
Nombre Tétraédrique — Un tétraèdre à 35 sphères. Chaque niveau représente un des 5 premiers nombres triangulaires. Un nombre tétraédrique, ou nombre pyramidal triangulaire, est un nombre figuré qui peut être représenté par une pyramide avec une base et trois côtés, c… … Wikipédia en Français
Nombre tetraedrique — Nombre tétraédrique Un tétraèdre à 35 sphères. Chaque niveau représente un des 5 premiers nombres triangulaires. Un nombre tétraédrique, ou nombre pyramidal triangulaire, est un nombre figuré qui peut être représenté par une pyramide avec une… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Nombre Pyramidal Carré