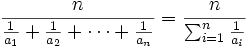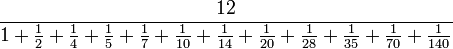- Nombre en division harmonique
-
Nombre à moyenne harmonique entière
Un nombre à moyenne harmonique entière est un nombre entier positif dont la moyenne harmonique des diviseurs est un entier. Autrement dit, si a1, a2, ..., an sont les diviseurs du nombre,
doit être un entier. Ces nombres ont été définis par Øystein Ore en 1948 et apparaissent dans la littérature mathématique anglophone sous différents noms, en particulier, Harmonic divisor number, Ore's (harmonic) numbers, harmonic numbers, numbers with integral harmonic mean [1] ; il ne semble pas y avoir de terminologie attestée en français.
Les premiers nombres à moyenne harmonique entière sont :
1, 6, 28, 140, 270, 496, 672, 1638, 2970, 6200, 8128, 8190, ...
Par exemple, le nombre 140 a pour diviseurs 1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, et 140. Leur moyenne harmonique est
donc est égale à 5, un entier.
Trois des nombres listés sont aussi des nombres parfaits. Ore démontra que tous les nombres parfaits sont de ce type. Comme les nombres parfaits, les nombres à moyenne harmonique entière tendent à être des nombres pairs, au moins dans les intervalles observés. Ore a en fait conjecturé qu'à part 1, il n'existe pas de nombres impairs à moyenne harmonique entière (une preuve de cette conjecture entraînerait la conjecture classique selon laquelle il n'existe pas de nombres parfaits impairs).
En 1972, W.H. Mills a démontré[2] qu'excepté 1, il n'existe pas de nombre impair à moyenne harmonique entière dont les facteurs premiers soient inférieurs à 107. En 2007, Y. Chishiki, T. Goto et Y. Ohno ont prouvé[3] que pour tout entier M, il existe au plus un nombre fini de nombres impairs à moyenne harmonique entière dont tous les facteurs premiers (à un nombre fixé près) sont bornés par M.
Références
- ↑ Cf. par exemple l'article correspondant sur WP:en ; M. Garcia, On numbers with integral harmonic mean, American Math. Monthly 61 (1954), 89-96 ; G. L. Cohen and Deng Moujie, On a generalisation of Ore's harmonic numbers, Nieuw. Arch. Wisk. (4)16 (1998), 161-172.
- ↑ W.H. Mills, On a conjecture of Ore, Proceedings of the 1972 Number Theory Conference, University of Colorado, Boulder, 1972, 142-146.
- ↑ Y. Chisiki, T. Goto, Y. Ohno, On the largest prime divisor of an odd harmonic number, Math. Comp. 76 (2007), 1577-1587.
Bibliographie
- Cohen, Graeme L., Numbers Whose Positive Divisors Have Small Integral Harmonic Mean, Mathematics of Computation 66 (1997), 883-891, cf. [1]
- Muskat, Joseph B., On Divisors of Odd Perfect Numbers, Mathematics of Computation 20 (1996), 141-144
- Ore, Øystein, On the averages of the divisors of a number, American Mathematical Monthly 55 (1948), 615-619
- (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Harmonic divisor number ».
Voir aussi
Ensembles d'entiers sur la base de leur divisibilité Formes de factorisation : Nombre premier · Nombre composé · Nombre puissant · Entier sans facteur carré Sommes de diviseurs : Nombre parfait · Nombre presque parfait · Nombre quasi parfait · Nombre parfait multiple · Nombre hyperparfait · Nombre parfait unitaire · Nombre semi-parfait · Nombre semi-parfait primitif · Nombre pratique Nombres de diviseurs : Nombre abondant · Nombre hautement abondant · Nombre superabondant · Nombre colossalement abondant · Nombre hautement composé Autres : Nombre déficient · Nombre étrange · Nombre amical · Nombre sociable · Nombre solitaire · Nombre sublime · Nombre à moyenne harmonique entière · Nombre frugal · Nombre équidigital · Nombre extravagant - Portail des mathématiques
Catégorie : Propriété arithmétique
Wikimedia Foundation. 2010.