Nombre Carré Centré

Nombre carré centré

Un nombre carré centré est un nombre figuré centré qui peut être représenté par un carré ayant un point en son centre et d'autres points placés autour du centre à une certaine distance (associée à la norme 1.) comme dans l'exemple suivant :

Zentrierte Quadratzahl.PNG

Pour tout entier strictement positif, le nombre carré centré de rang n est égal à :

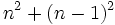$n^2 + (n - 1)^2\,$ .

Autrement dit, un nombre carré centré est la somme de deux nombres carrés consécutifs. La figure suivante illustre bien ce fait :

Zentrierte Quadratzahl2.PNG

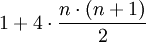$1 + 4\cdot \frac{n\cdot (n+1)}{2}$ .

Zentrierte Quadratzahl3.PNG

Les nombres carrés centrés peuvent aussi s'écrire sous la forme suivante (où n est un entier impair) :

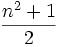${{n^2 + 1} \over 2}\,$ .

Les quatre premières valeurs de n (1,3,5,7) sont figurées ci-dessous. La figure est formée en considérant un carré de n point par points, et en sélectionnant la moitié des points, à partir du coin supérieur gauche, jusqu'au point central inclus.

*   ***  *****  *******
    **   *****  *******
         ***    *******
                ****

Les quelques premiers nombres carrés centrés sont :

1, 5, 13, 25, 41, 61, 85, 113, 145, 181, 221, 265, 313, 365, 421, 481, 545, 613, 685, 761, 841, 925, 1013, 1105, 1201, 1301, 1405, 1513, 1625, 1741, 1861, 1985, 2113, 2245, 2381, 2521, 2665, 2813, 2965, 3121, 3281, 3445, 3613, 3785, 3961, 4141, 4325, ...

Tous les nombres carrés centrés sont impairs, et en base 10 nous pouvons remarquer que leurs chiffres des unités suivent le modèle 1-5-3-5-1.

Tous les nombres carrés centrés et leurs diviseurs ont reste égal à un lorsqu'ils sont divisés par quatre. Ainsi tous les nombres carrés centrés et leurs diviseurs se terminent par le chiffre 1 ou 5 en base 6, 8 et 12.

Voyez également

Nombre carré

Portail des mathématiques

Ce document provient de « Nombre carr%C3%A9 centr%C3%A9 ».

Catégorie : Nombre figuré

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Nombre Carré Centré de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Nombre carre centre — Nombre carré centré Un nombre carré centré est un nombre figuré centré qui peut être représenté par un carré ayant un point en son centre et d autres points placés autour du centre à une certaine distance (associée à la norme 1.) comme dans l… … Wikipédia en Français
Nombre carré centré — Un nombre carré centré est un nombre figuré centré qui peut être représenté par un carré ayant un point en son centre et d autres points placés autour du centre à une certaine distance (associée à la norme 1.) comme dans l exemple suivant :… … Wikipédia en Français
Nombre Carré — Carré parfait En mathématiques, un entier n est un carré parfait (un carré s il n y a pas ambiguïté) s il existe un entier k tel que n = k2 ; en d autres termes, un carré parfait est le carré d un entier. Par exemple, les entiers 0, 1, 4 ou… … Wikipédia en Français
Nombre carre — Carré parfait En mathématiques, un entier n est un carré parfait (un carré s il n y a pas ambiguïté) s il existe un entier k tel que n = k2 ; en d autres termes, un carré parfait est le carré d un entier. Par exemple, les entiers 0, 1, 4 ou… … Wikipédia en Français
Nombre carré — Carré parfait En mathématiques, un entier n est un carré parfait (un carré s il n y a pas ambiguïté) s il existe un entier k tel que n = k2 ; en d autres termes, un carré parfait est le carré d un entier. Par exemple, les entiers 0, 1, 4 ou… … Wikipédia en Français
Nombre Polygonal Centré — Un nombre polygonal centré est un type de nombre figuré, qui peut être représenté par une figure plane ayant un point placé en son centre et tous les autres points disposés autour de ce centre formant des couches polygonales successives avec un… … Wikipédia en Français
Nombre polygonal centre — Nombre polygonal centré Un nombre polygonal centré est un type de nombre figuré, qui peut être représenté par une figure plane ayant un point placé en son centre et tous les autres points disposés autour de ce centre formant des couches… … Wikipédia en Français
Nombre Octogonal Centré — En mathématiques, un nombre octogonal centré est un nombre figuré centré qui représente un octogone avec un point au centre et tous les autres points entourant le centre en couches successives. Le nombre octogonal centré pour n est donné par la… … Wikipédia en Français
Nombre octogonal centre — Nombre octogonal centré En mathématiques, un nombre octogonal centré est un nombre figuré centré qui représente un octogone avec un point au centre et tous les autres points entourant le centre en couches successives. Le nombre octogonal centré… … Wikipédia en Français
Nombre Triangulaire Centré — Un nombre triangulaire centré est un nombre figuré centré qui peut être représenté par un triangle avec un point placé en son centre et tous les autres points disposés autour de ce centre. Le nombre triangulaire centré de rang n est égal à L… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Nombre Carré Centré