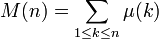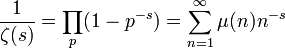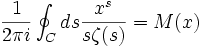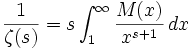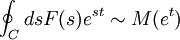Fonction De Mertens

Fonction De Mertens

Fonction de Mertens

En théorie des nombres, la fonction de Mertens est

M(n) = \sum_{1\le k \le n} \mu(k)

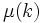où \mu(k)\, est la fonction de Möbius.

La fonction de Möbius retourne seulement les valeurs -1, 0 et +1, il est évident que la fonction de Mertens croît lentement et qu'il n'existe pas de x tel que M(x) > x. La conjecture de Mertens (1897) va même plus loin, énonçant qu'il n'existe pas de x où la valeur absolue de la fonction de Mertens excède la racine carrée de x. Odlyzko et Te Riele ont montré (1985) que cette conjecture était fausse. Néanmoins, l'hypothèse de Riemann est équivalente à une conjecture plus faible sur la croissance de M(x), explicitement 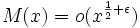M(x) = o(x^{\frac12 + \epsilon})\,. Puisque les valeurs élevées de M croissent au moins aussi rapidement que la racine carrée de x, ceci place une limite plutôt serrée sur le taux de croissance. Ici, o fait référence à la notation de Landau. On ne connaît pas aujourd'hui de contre-exemple explicite à cette conjecture, mais on sait qu'il en existe au moins un entre 1012 et 3,211 1064 (Pintz, 1987).

La fonction Möbius est implémentée dans Mathematica, mais pas la fonction de Mertens, mais elle peut être définie par cette commande :

Mertens[x_] := Plus @@ MoebiusMu[Range[1, x]]

Sommaire

Représentations intégrales

En utilisant le produit eulérien, on trouve que

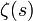\frac{1}{\zeta(s) }= \prod_{p} (1-p^{-s})= \sum_{n=1}^{\infty}\mu (n)n^{-s}

où \zeta(s)\, est la fonction zeta de Riemann et le produit pris sur les nombres premiers. Alors, en utilisant cette série de Dirichlet avec la formule de Perron, on obtient :

\frac{1}{2\pi i}\oint_{C}ds \frac{x^{s}}{s\zeta(s) }=M(x)

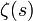où "C" est une courbe fermée encerclant toutes les racines de \zeta(s)\,.

Inversement, on a la transformée de Mellin

\frac{1}{\zeta(s)} = s\int_1^\infty \frac{M(x)}{x^{s+1}}\,dx

qui reste valable pour Re(s)>1\,.

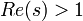Une bonne évaluation, au moins asymptotiquement, serait d'obtenir, par la méthode de descente par gradient, une inégalité :

\oint_{C}dsF(s)e^{st} \sim M(e^{t})

Calcul

La fonction de Mertens a été calculée pour un intervalle de plus en plus grand de n.

Personne Année Limite
Mertens 1897 104
von Sterneck 1897 1,5 x 105
von Sterneck 1901 5 x 105
von Sterneck 1912 5 x 106
Neubauer 1963 108
Cohen et Dress 1979 7,8 x 109
Dress 1993 1012
Lioen et van der Lune 1994 1013
Kotnik et van der Lune 2003 1014

Références

  • Pintz J, An effective disproof of the Mertens conjecture, Astérisque 147-148, 325-333 and 346 (1987).
  • Odlyzko AM, te Riele HJJ, Disproof of the Mertens conjecture, J. reine angew. Math. 357, 138-160 (1985).

Liens externes

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Fonction de Mertens ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonction De Mertens de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Fonction de mertens — En théorie des nombres, la fonction de Mertens est où est la fonction de Möbius. La fonction de Möbius retourne seulement les valeurs 1, 0 et +1, il est évident que la fonction de Mertens croît lentement et qu il n existe pas de x tel que M(x)… …   Wikipédia en Français

  • Fonction de Mertens — En théorie des nombres, la fonction de Mertens est où est la fonction de Möbius. Puisque la fonction de Möbius ne prend que les valeurs 1, 0 et +1, il est évident qu il n existe pas de x tel que |M(x)| > x. La conjecture de Mertens (1897) va… …   Wikipédia en Français

  • Fonction Zeta de Riemann — Fonction zêta de Riemann En mathématiques, la fonction ζ de Riemann est une fonction analytique complexe qui est apparue essentiellement dans la théorie des nombres premiers. La position de ses zéros complexes est liée à la répartition des… …   Wikipédia en Français

  • Fonction Zêta De Riemann — En mathématiques, la fonction ζ de Riemann est une fonction analytique complexe qui est apparue essentiellement dans la théorie des nombres premiers. La position de ses zéros complexes est liée à la répartition des nombres premiers. Elle est… …   Wikipédia en Français

  • Fonction dzêta de Riemann — Fonction zêta de Riemann En mathématiques, la fonction ζ de Riemann est une fonction analytique complexe qui est apparue essentiellement dans la théorie des nombres premiers. La position de ses zéros complexes est liée à la répartition des… …   Wikipédia en Français

  • Fonction zeta de Riemann — Fonction zêta de Riemann En mathématiques, la fonction ζ de Riemann est une fonction analytique complexe qui est apparue essentiellement dans la théorie des nombres premiers. La position de ses zéros complexes est liée à la répartition des… …   Wikipédia en Français

  • Fonction zéta — Fonction zêta de Riemann En mathématiques, la fonction ζ de Riemann est une fonction analytique complexe qui est apparue essentiellement dans la théorie des nombres premiers. La position de ses zéros complexes est liée à la répartition des… …   Wikipédia en Français

  • Fonction zêta de riemann — En mathématiques, la fonction ζ de Riemann est une fonction analytique complexe qui est apparue essentiellement dans la théorie des nombres premiers. La position de ses zéros complexes est liée à la répartition des nombres premiers. Elle est… …   Wikipédia en Français

  • Fonction zêta de Riemann — La fonction zêta de Riemann ζ(s) dans le plan complexe. La couleur d un point s code la valeur de ζ(s) : des couleurs vives indiquent des valeurs proches de 0 et la nuance indique l argument de la valeur. Le point blanc pour s = 1… …   Wikipédia en Français

  • Mertens — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Patronyme Le nom de Mertens est porté par plusieurs personnalités (par ordre alphabétique) : Franz Mertens (1840 1927), mathématicien allemand. Franz …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”